Calculer le ratio de cohérence pour la comparaison par paires

L’outil Attribuer des pondérations via une comparaison par paires calcule les pondérations relatives pour un ensemble de variables en entrée en les comparant par paires. Une fonctionnalité de diagnostic est mise à disposition et permet de vérifier que les évaluations de comparaison entre les paires sont logiquement cohérentes. L’outil calcule le ratio de cohérence (RC) pour vous aider à améliorer la cohérence de vos évaluations. Par exemple, vos évaluations de comparaison par paires seront incohérentes si vous classez la variable A comme étant deux fois plus importante que la variable B, la variable B comme étant deux fois plus importante que la variable C et la variable C comme étant de la même importance que la variable A. En d’autres termes, si A > B et B > C, alors C ne peut pas être égal à A.

En conservant un ratio de cohérence dans les limites acceptables, vous évitez des classements incohérents. D’après Saaty (2000) :

• Si le ratio de cohérence est supérieur ou égal à 0,1, la cohérence de la comparaison par paires est acceptable.
• Si le ratio de cohérence est supérieur à 0,1, il est recommandé d’ajuster les évaluations de comparaison pour améliorer la cohérence.

Traitement du calcul du ratio de cohérence

Les étapes permettant de calculer le ratio de cohérence (RC) sont les suivantes :

• L’indice de cohérence (IC) est calculé.
• L’indice aléatoire (IA) est déterminé en fonction du nombre de variables.
• Le ratio de cohérence (RC) est calculé en divisant l’indice de cohérence (IC) par l’indice aléatoire (IA).

La matrice de comparaison suivante sera utilisée dans un exemple illustrant le calcul du ratio de cohérence pour cinq variables.

Tableau 1 : matrice de comparaison avec pondérations dérivées.

Variable	Solar_Gain	Aspect	Elevation	Dist_to_Road	Dist_to_Elect	Pondérations
Solar_Gain	1	3	2	2	0,333	0,235
Aspect	0,333	1	0,5	1	0,2	0,089
Elevation	0,5	2	1	1	0,5	0,136
Dist_to_Road	0,5	1	1	1	5	0,247
Dist_to_Elect	3	5	2	0,2	1	0,294

Les équations décrites ci-dessous sont utilisées dans les calculs.

Calculer l’indice de cohérence (IC)

L’indice de cohérence (IC) est calculé avec la formule suivante :

Où :

• λ (la valeur propre principale) est la moyenne de λ_i pour chaque variable
• n est le nombre de variables en entrée

La valeur λ_i pour chaque variable est calculée avec la formule suivante :

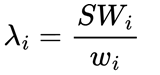
Où :

• p_i indique les pondérations dérivées pour chaque variable en entrée (la colonne Pondérations dans le tableau 1)
• SP_i est la somme pondérée pour chaque variable i

La somme pondérée pour chaque variable est calculée avec la formule suivante :

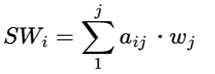
Où :

• a_ij est la valeur issue de la matrice de comparaison par paires originale, où i désigne la ligne et j désigne la colonne
• pj sont les pondérations dérivées des variables correspondantes

Par exemple, la valeur SP pour la ligne de la variable Solar_Gain est calculée comme suit :

La valeur λ_i pour la variable Solar_Gain est calculée comme suit :

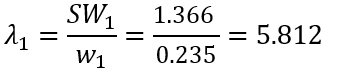
Effectuez les calculs pour chaque ligne afin de trouver la valeur λ_i pour chaque variable.

Ensuite, faites la moyenne des valeurs λ_i pour obtenir λ.

Dans cet exemple, λ a pour valeur 6,462, comme spécifié dans le tableau ci-dessous.

Tableau 2 : calcul de la somme pondérée (SP) et de λ_i pour chaque variable.

Variable	Pondérations(pi)	Somme pondérée(SPi)	λi = SPi / pi
Solar_Gain	0,235	1,366	5,812
Aspect	0,089	0,541	6,079
Elevation	0,136	0,826	6,070
Dist_to_Road	0,247	2,060	8,338
Dist_to_Elect	0,294	1,765	6,005
Moyenne	N/D	N/D	6,462

Maintenant que λ a été calculé, vous pouvez calculer l’IC avec la formule fournie ci-dessus.

Étant donné que le nombre de variables dans cet exemple est 5, la valeur de l’IC est calculée comme suit :

IC = (6,462 - 5)/(5 - 1) = 0,365

Calculer l’indice aléatoire (IA)

L’indice aléatoire (IA) est une valeur statistique prédéfinie qui sert de référence pour le calcul du ratio de cohérence pour les comparaisons par paires. Développées par Saaty (2000), les valeurs d’indice aléatoire (IA) sont dérivées d’une simulation de Monte-Carlo pour chaque taille de matrice. Les valeurs d’indice aléatoire (IA) dérivées pour chaque taille de matrice sont présentées dans le tableau ci-dessous. Les tailles de matrice sont indiquées sur la première ligne.

Taille de la matrice	2	3	4	5	6	7	8	9
IA	0	0,58	0,90	1,12	1,24	1,32	1,41	1,45

La valeur d’indice aléatoire (IA) est 0 pour la comparaison de deux variables car la comparaison est intrinsèquement cohérente. Les valeurs d’indice aléatoire (IA) augmentent avec le nombre de variables en entrée.

Dans cet exemple, le nombre de variables est 5. Par conséquent, la valeur d’indice aléatoire (IA) correspondante est 1,12.

Calculer le ratio de cohérence (RC)

Le ratio de cohérence (RC) est calculé en divisant l’indice de cohérence (IC) par l’indice aléatoire (IA). Cette valeur de ratio de cohérence (RC) indique dans quelle mesure les comparaisons par paires sont cohérentes.

Dans cet exemple, le ratio de cohérence (RC) est calculé comme suit :

RC = 0,365/1,12 = 0,326

Étant donné que la valeur du ratio de cohérence est supérieure à 0,1, il est recommandé de modifier les évaluations de comparaison pour améliorer la cohérence.

Améliorer la cohérence

S’il est établi que les comparaisons des variables en entrée sont incohérentes, les trois paires qui contribuent le plus à l’incohérence sont mises en évidence. Il est recommandé d’ajuster les paires mises en évidence pour améliorer la cohérence.

Le processus ci-dessous permet d’identifier les trois paires les plus incohérentes.

Construire une matrice de cohérence par paires

Construisez une matrice qui sera utilisée pour l’évaluation de la cohérence par paires (Saaty, 2003). Cette matrice est désignée par ε_ij dans la formule suivante :

Où :

• a_ij est la valeur issue de la matrice de comparaison par paires originale, i désigne la ligne et j désigne la colonne
• p_j et p_i sont les pondérations dérivées pour les variables j et i.

Calculer les valeurs

Une fois la matrice construite, les trois valeurs les plus élevées dans la matrice ε_ij sont identifiées. Les variables de ligne et de colonne correspondantes sont considérées comme des paires incohérentes.

Dans cet exemple de comparaison, la valeur de ratio de cohérence (RC) est supérieure à 0,1 (0,326). Pour identifier les paires incohérentes, la valeur ε_ij pour la cellule à l’intersection de la ligne Solar_Gain et de la colonne Aspect est calculée comme suit :

Effectuez le calcul pour toutes les cellules.

Identifier les paires les plus incohérentes

La matrice ε_ij pour l’exemple de comparaison ci-dessus est construite comme suit :

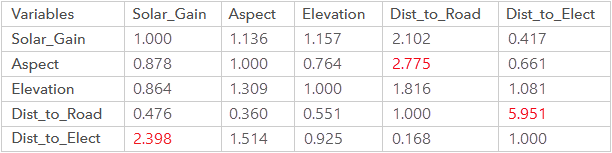
Les trois valeurs les plus élevées dans la matrice sont les comparaisons qui contribuent le plus à l’incohérence. Il s’agit des évaluations de comparaison pour les variables Dist_to_Road et Dist_to_Elect, pour les variables Aspect et Dist_to_Road et pour les variables Dist_to_Elect et Solar_Gain. Les trois paires sont mises en évidence en rouge des deux cotés des curseurs dans la boîte de dialogue de l’outil.

Dans la matrice de comparaison originale, la variable Solar_Gain est évaluée comme étant deux fois plus importante que Dist_to_Road (Solar_Gain > Dist_to_Road) et trois fois moins importante que Dist_to_Elect (Dist_to_Elect > Solar_Gain). Logiquement, Dist_to_Road devrait être moins importante que Dist_to_Elect (Dist_to_Elect > Dist_to_Road). Cependant, dans la comparaison originale, l’évaluation attribue incorrectement à Dist_to_Road une pondération cinq fois plus importante que celle de Dist_to_Elect (Dist_to_Road > Dist_to_Elect). Il s’agit de la cause principale de l’incohérence.

Pour corriger cette erreur, faites glisser le curseur vers Dist_to_Elect et revérifiez le ratio de cohérence. Par exemple, si vous faites glisser le curseur à la position 5 du côté de Dist_to_Elect et cliquez à nouveau sur le bouton Cohérence, le nouveau ratio de cohérence est 0,029, ce qui indique que la comparaison globale est désormais cohérente.

Bibliographie

Saaty, T. L. 2000. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. Pittsburgh, PA: RWS Publications

Saaty, T. L. 2003. "Decision-making with the AHP: Why is the principal eigenvector necessary". European Journal of Operational Research, 145(1), 85-91.