Fonctionnement des fonctions de base radiale

Disponible avec une licence Geostatistical Analyst.

Les fonctions de base radiale (RBF) sont une série de techniques d’interpolation précises. En d’autres termes, la surface doit traverser chaque valeur d’échantillonnage mesurée. Les fonctions de base sont les suivantes :

• Spline de plaque mince
• Spline avec tension
• Spline entièrement régularisée
• Fonction multiquadratique
• Fonction multiquadratique inverse

Chaque fonction de base présente une forme différente et produit une surface d’interpolation différente. Les méthodes RBF sont un cas particulier de splines.

En théorie, les méthodes RBF s’apparentent à l’ajustement d’une membrane caoutchoutée à travers les valeurs d’échantillonnage mesurée tout en réduisant la courbure totale de la surface. La fonction de base que vous sélectionnez détermine la façon dont la membrane caoutchoutée s’ajustera entre les valeurs. L’image suivante est une illustration théorique de la façon dont une surface RBF s’ajuste à travers une série de valeurs d’échantillonnage d’élévation. Notez que dans la coupe transversale, la surface passe par les valeurs de données.

La coupe transversale montre comment la surface RBF s’ajuste à travers les valeurs d’échantillonnage.

Considérées comme précises, les méthodes RBF diffèrent des méthodes d’interpolation polynomiales globales et locales, qui sont toutes les deux de nature inexacte et qui n’exigent pas que la surface passe à travers les points mesurés. Par comparaison avec une méthode RBF, l’interpolateur IDW (Inverse Distance Weighted, Pondération par l’inverse de la distance), qui est lui-même un interpolateur exact, ne prévoit jamais de valeurs supérieures à la valeur mesurée maximale ou de valeurs inférieures à la valeur mesurée minimale comme illustré dans la coupe transversale d’un transect de données d’échantillonnage ci-dessous.

Cependant, les méthodes RBF peuvent prévoir des valeurs supérieures aux valeurs mesurées maximales et des valeurs inférieures aux valeurs mesurées minimales comme illustré dans la coupe transversale ci-dessous.

Les paramètres optimaux sont déterminés à l’aide d’une validation croisée comme expliqué pour l’interpolation polynomiale locale et IDW.

Quand utiliser les fonctions de base radiale

Les fonctions de base radiale permettent de produire des surfaces lisses à partir d’un grand nombre de points de données. Elles produisent de bons résultats pour les surfaces variant doucement, telles que l’élévation.

Ces techniques sont toutefois inappropriées en cas de variations importantes des valeurs de surface à de courtes distances ou lorsque vous soupçonnez que les données d’échantillonnage sont sujettes à l’incertitude ou aux erreurs de mesure.

Concepts inhérents aux fonctions de base radiale

Dans l’ArcGIS Geostatistical Analyst extension, des fonctions de base radiales se forment sur chaque localisation de données. Une fonction de base radiale est une fonction qui change avec la distance par rapport à une localisation, comme illustré dans l’image ci-dessous.

Des fonctions RBF pour différentes localisations sont illustrées.

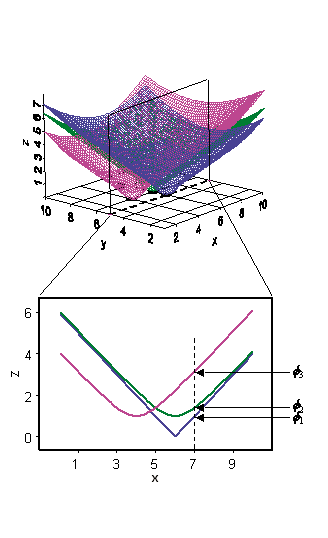
Supposons par exemple que la fonction de base radiale soit simplement la distance par rapport à chaque localisation. Elle forme ainsi un cône inversé sur chaque localisation. Si vous prenez une coupe transversale du plan x,z pour y = 5, vous verrez une tranche de chaque fonction de base radiale. Supposons maintenant que vous souhaitez prévoir une valeur à y = 5 et x = 7. La valeur de chaque fonction de base radiale à la localisation de la prévision peut être tirée de la figure ci-dessus, indiquée par les valeurs Φ₁, Φ₂ et Φ₃ qui dépendent de la distance par rapport à chaque localisation de données. La méthode de prévision est formée en prenant la moyenne pondérée w₁Φ₁ + w₂Φ₂ + w₃Φ₃ + …

Vous devez à présent déterminer les pondérations. Jusqu’à maintenant, vous n’avez pas du tout utilisé les valeurs de données. Les pondérations w₁, w₂, w₃, etc, sont identifiées en demandant que la valeur de données soit prévue de façon exacte lorsque la prévision est déplacée sur une localisation avec une valeur exacte. Cela forme N équations avec N inconnues et une résolution unique. La surface passe donc par les valeurs de données, ce qui assure l’exactitude des prévisions.

La fonction de base radiale dans cet exemple est un cas particulier de la fonction RBF multiquadratique. Dans Geostatistical Analyst, vous pouvez également utiliser d’autres fonctions RBF telles que les splines entièrement régularisées, les splines de plaque mince, les splines avec tension et la fonction multiquadratique inverse. Parfois, la différence entre ces fonctions n’est pas évidente. Vous pouvez avoir une raison valable d’une choisir une spécifique, mais vous pouvez aussi utiliser la validation croisée pour en décider. Chacune des fonctions RBF dispose d’un paramètre qui contrôle le lissage de la surface.

Pour toutes les méthodes à l’exception de la fonction multiquadratique inverse, plus la valeur du paramètre est élevée, plus la carte est lisse. L’opposé est vrai pour la fonction multiquadratique inverse.