Les distributions suivantes sont disponibles pour un ensemble d’outils qui génèrent des valeurs aléatoires. Les distributions transforment les valeurs aléatoires 0 à 1 créées à partir du flux spécifié (identifié globalement dans l’environnement d’analyse ou localement dans l’outil) vers la distribution spécifiée. Reportez-vous à la rubrique Syntaxe de distribution des valeurs aléatoires pour connaître la syntaxe et les paramètres de chaque distribution.
Distribution uniforme
La distribution uniforme est une distribution de probabilité continue dans laquelle toutes les valeurs situées à un intervalle spécifié ont la même probabilité. Une distribution d’entiers est une version discrète de la distribution uniforme (voir ci-dessous). La distribution uniforme peut être utilisée lors de la modélisation des concentrations d’un gaz dans un modèle de simulation ou du temps écoulé entre des accidents à une intersection, ainsi que pour positionner les points dans l’outil Créer des points aléatoires.
La distribution uniforme est souvent utilisée pour modéliser des événements aléatoires lorsque chaque occurrence ou résultat potentiel a une probabilité égale de se produire.
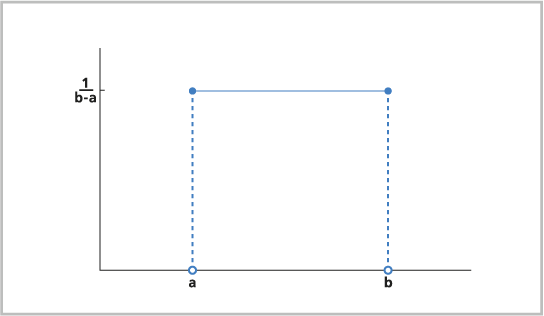
La formule de la distribution uniforme est la suivante :
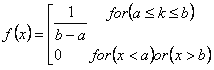
où
a est la valeur minimale de l’intervalle avec une probabilité égale.
b est la valeur maximale de l’intervalle avec une probabilité égale.
x désigne les observations.
Les valeurs aléatoires sélectionnées sont comprises entre les valeurs minimale et maximale (mutuellement exclusives). La valeur minimale doit être inférieure à la valeur maximale Si aucune valeur minimale et maximale n’est fournie, des variables uniformes comprises entre 0,0 et 1,0 sont produites.
Distribution d’entiers
La distribution d’entiers est une distribution de probabilité dans laquelle toutes les valeurs discrètes situées à un intervalle spécifié ont la même probabilité. La distribution d’entiers est la version discrète de la distribution uniforme (voir ci-dessus). La distribution d’entiers peut être utilisée pour modéliser la probabilité d’apparition de chaque nombre lors d’un lancer de dé (chaque nombre a une probabilité d’un sixième de se produire), modéliser des événements aléatoires dans un modèle de simulation ou sélectionner des localisations d’échantillonnage pour une étude biologique.
La distribution d’entiers est utilisée souvent pour modéliser des événements aléatoires lorsque chaque occurrence ou résultat potentiel a une probabilité égale de se produire.

La formule de la distribution d’entiers est illustrée ici :
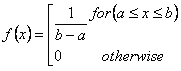
où
a est la valeur minimale de l’intervalle avec une probabilité égale.
b est la valeur maximale de l’intervalle avec une probabilité égale.
x désigne les observations.
Les valeurs aléatoires sélectionnées sont comprises entre les valeurs minimale et maximale (mutuellement exclusives). La valeur minimale doit être inférieure à la valeur maximale Si aucune valeur minimale et maximale n’est fournie, des valeurs uniformes comprises entre 1 et 100 sont produites.
Distribution normale
La distribution normale modélise les variables aléatoires continues qui se produisent couramment. La distribution normale est largement utilisée et est disponible dans de nombreuses applications. Elle s’appuie sur le théorème de la limite centrale, qui repose sur le principe suivant : la somme des variables aléatoires est normalement distribuée si le nombre d’observations est important. Par exemple, le nombre de fois où le côté face apparaît dans une séquence de tirages à pile ou face approche la normalité si la pièce est lancée de nombreuses fois. Les distributions normales sont par exemple la taille des gens dans un pays, les valeurs d’élévation dans un état et les résultats d’un examen de mathématiques pour tous les élèves de 12 ans.
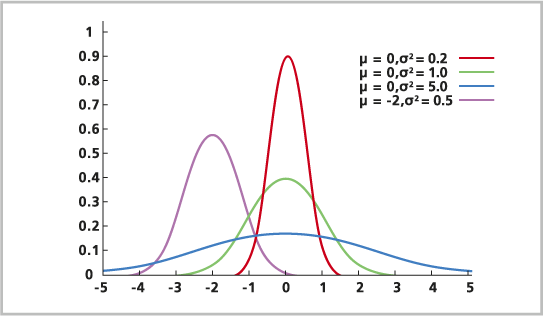
La formule de la distribution normale est la suivante :

où
μ est la moyenne.
σ est l’écart type (nombre positif).
La distribution normale est symétrique par rapport à la moyenne, au mode et à la médiane, qui sont tous égaux à μ.
Les distributions binomiales et Poisson modélisent souvent des événements futurs discrets, indépendants, aléatoires, vrais ou faux (par exemple, le nombre de fois où le côté face apparaît lorsque vous lancez une pièce) à l’aide d’un nombre relativement petit d’observations, tandis que la distribution normale modélise des variables continues (par exemple, la hauteur, la pondération et la quantité) à l’aide d’un grand nombre d’observations. Les distributions binomiales et Poisson reposent sur une probabilité, tandis que la distribution normale est le nombre d’observations qui correspondent à la quantité ou magnitude.
Distribution exponentielle
La distribution exponentielle est une distribution de probabilité continue. Elle est généralement utilisée pour modéliser le temps écoulé entre des événements qui se produisent à un rythme moyen constant, ou pour modéliser l’occurrence d’événements dans une distance par unité. Le temps écoulé avant le prochain accident à une intersection, le temps écoulé entre l’observation de deux étoiles filantes dans le ciel nocturne et la distance entre deux nids-de-poule dans une rue sont tous des exemples dans lesquels la distribution exponentielle peut être utilisée. Avec chacun de ces exemples, à mesure que le temps ou la distance augmente, la probabilité est exponentiellement plus importante que l’état change ou l’événement se produise. Les occurrences des événements sont indépendantes les unes des autres.
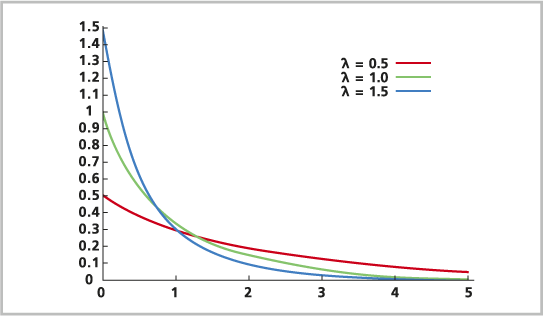
La formule de la distribution exponentielle est la suivante :
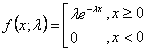
où
e est le logarithme naturel.
x est le nombre possible d’occurrences pour l’événement (valeurs entières positives).
La distribution exponentielle modélise les traitements Poisson où le phénomène est à un état initial. La distribution exponentielle est la version continue de la distribution géométrique. Si la progression de l’état A à l’état B peut être décomposée en plusieurs tâches indépendantes, il peut être préférable de la modéliser avec la distribution gamma. La distribution gamma modélise la somme de plusieurs variables indépendantes distribuées de façon exponentielle. Elle peut être considérée comme un cas particulier de la distribution exponentielle.
Distribution Poisson
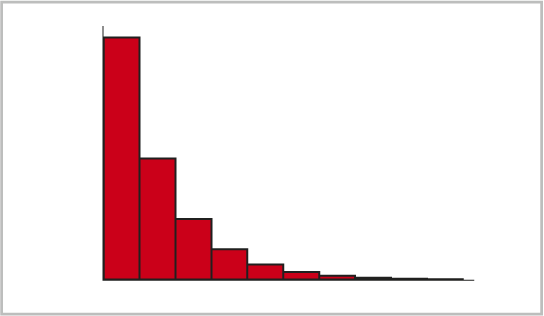
La distribution Poisson est une distribution de probabilité discrète. La distribution Poisson modélise la probabilité que le nombre d’événements se produisent au cours d’un intervalle temporel fixe, étant donné une moyenne connue. Les événements sont indépendants de la dernière fois qu’ils se sont produits. Sur l’axe x se trouvent les valeurs discrètes des événements 0, 1, 2, 3, 4 et ainsi de suite (représentant souvent le nombre de fois que l’événement se produit) et sur l’axe y se trouve la probabilité que le phénomène survienne ce nombre de fois, étant donné une moyenne connue. Les événements peuvent être le nombre d’accidents à une intersection, le nombre d’anomalies congénitales ou le nombre d’élans dans un kilomètre carré. La distribution Poisson modélise les occurrences rares. La distribution est parfois appelée loi des petits nombres car l’événement ne se produit pas souvent, mais il existe de nombreuses opportunités pour qu’il se produise.

La formule est la suivante :
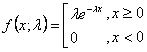
où
e est le logarithme naturel.
k est le nombre possible d’occurrences pour l’événement (valeurs entières positives).
k! est la fonction factorielle de k.
λ (ou la moyenne) est le nombre positif représentant le nombre d’occurrences attendu au sein d’un intervalle spécifié. Si l’événement se produit toutes les 10 minutes dans une heure (60 minutes), la valeur lambda est égale à 6.
La distribution Poisson est similaire à la distribution binomiale, mais la distribution Poisson modélise l’occurrence d’un événement rare sans connaître d’informations sur le nombre total d’occurrences possibles. La distribution Poisson examine le nombre d’accidents à une intersection, tandis que la distribution binomiale modélise le nombre d’accidents par rapport au nombre de voitures qui traversent l’intersection.
Distribution gamma
La distribution gamma est une distribution de probabilité continue. La distribution gamma modélise la somme de plusieurs variables indépendantes distribuées de façon exponentielle. Elle peut être considérée comme un cas particulier de la distribution exponentielle.
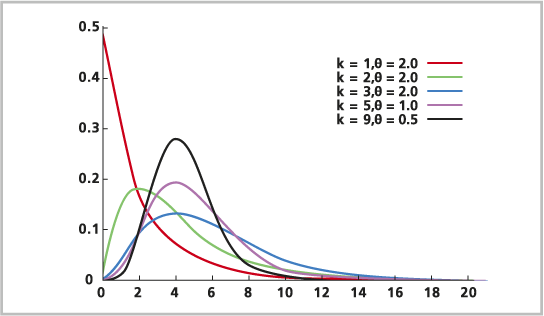
La formule de la distribution gamma est la suivante :

Voici une autre méthode pour paramétrer la distribution gamma :

Si la valeur alpha est égale à 1, la distribution gamma est égale à la distribution exponentielle. Lorsque la valeur alpha est un entier, la distribution gamme devient la distribution d’Erlang. Pour une valeur alpha entière et une valeur bêta égale à 2, la distribution gamma devient une distribution du Khi-deux avec 2 degrés alpha de liberté.
Les variables obtenues sont supérieures ou égales à 0,0. Les valeurs alpha et bêta doivent être supérieures à 0,0.
Distribution binomiale
La distribution binomiale modélise le nombre d’occurrences d’un événement lors de l’observation d’une séquence de producteurs potentiels de l’événement. Par exemple, la distribution binomiale capture le nombre de personnes dans une étude clinique qui sont décédées d’une maladie cardiaque, le nombre de personnes qui descendent au deuxième étage d’un ascenseur bondé ou le nombre d’animaux dans une population qui présentent une certaine caractéristique génétique.

La distribution binomiale décrit les occurrences, et non la magnitude. Elle peut modéliser le nombre de participants qui ont terminé une course, pas leur vitesse.
La formule de la distribution binomiale est la suivante :
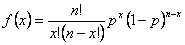
où
n est le nombre d’observations.
p est la probabilité d’occurrence.
x est le nombre de réussites, compris entre 0 et n.
Par exemple, la distribution binomiale permet de déterminer la probabilité du nombre de fois qu’une pièce lancée en l’air 10 fois retombe sur le côté face (n = 10). Le résultat peut être de 0 côté face sur 10, 1 sur 10 et ainsi de suite. Par conséquent, x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Et p est la probabilité de chaque x.
Tous les essais sont indépendants et chaque essai conduit à une réussite ou à un échec.
La distribution binomiale est proche de la distribution Poisson pour une valeur n élevée et une valeur p faible. Dans ce cas, il est peut-être plus simple d’utiliser la distribution Poisson.
La distribution binomiale renvoie une variable aléatoire pour le nombre de réussites sur n essais, où la probabilité de réussite dans chaque essai est égale à p (par exemple, la probabilité que le côté face apparaisse correspond à p).
Distribution géométrique
La distribution géométrique est une distribution de probabilité discrète. Il existe deux types principaux de phénomènes que cette distribution modélise : (1) la probabilité du nombre de fois nécessaires pour parvenir à une réussite (par exemple, le nombre de lancers de dés nécessaires pour obtenir un 6) ou (2) la probabilité du nombre d’échecs avant de parvenir à une réussite (par exemple, le nombre de randonnées nécessaires sur un sentier avant d’apercevoir un cerf). La probabilité de ne pas apercevoir un cerf lors de la première randonnée sur le sentier est de (1 - p). Pour la deuxième randonnée, la probabilité de ne pas apercevoir un cerf est de (1 - p) (1 - p). À mesure que le nombre de randonnées sur le sentier augmente, la probabilité de ne pas apercevoir un cerf décroît de façon exponentielle, et un cerf finira par être aperçu. Les événements sont indépendants les uns des autres.
La formule de la distribution géométrique est la suivante :

où
p est la probabilité de réussite.
n est le nombre d’essais.
La distribution géométrique est la version discrète de la distribution exponentielle (voir ci-dessus). La distribution géométrique est un cas particulier de la distribution Pascal ou binomiale négative, avec r dans la distribution Pascal qui est égal à 1 (voir ci-dessous).
Distribution binomiale négative
La distribution binomiale négative est une distribution de probabilité discrète. La distribution binomiale négative repose sur des essais de Bernoulli. Les essais de Bernoulli modélisent l’expérience au cours de laquelle les essais n’ont que deux résultats possibles (réussite ou échec), ont une probabilité de réussite, p (p étant identique pour chaque essai) et sont indépendants les uns des autres. Le lancer d’une pièce à pile ou face est une épreuve de Bernoulli. Par exemple, la distribution binomiale négative peut modéliser le nombre de lancers nécessaires de la pièce avant qu’elle atterrisse cinq fois de suite sur le côté face. Ainsi, la distribution binomiale négative modélise le nombre d’échecs avant une réussite. Lorsque r est un entier, la distribution binomiale négative devient un cas particulier connu sous le nom de distribution Pascal.
La formule de la distribution binomiale négative est la suivante :
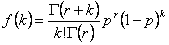
où
r est le nombre d’échecs.
p est la probabilité de réussite.
k est le nombre de réussites, compris entre 0 et n.
Lorsque la distribution binomiale négative représente un tirage à pile ou face, une valeur aléatoire est renvoyée pour le nombre de fois nécessaires avant que le côté face apparaisse.
Vous avez un commentaire à formuler concernant cette rubrique ?