Disponible avec une licence Standard ou Advanced.
Une topologie est un ensemble de règles qui, associée à un jeu d'outils et de techniques de mise à jour, permet à la géodatabase de modéliser plus précisément les relations géométriques. ArcGIS implémente la topologie via un ensemble de règles qui définissent la manière dont les entités peuvent partager un espace géographique et un jeu d'outils de mise à jour fonctionnant avec les entités qui partagent la géométrie d'une manière intégrée. Une topologie est stockée dans une géodatabase sous forme d'une ou de plusieurs relations qui définissent la manière dont les entités d'une ou plusieurs classes d'entités partagent la géométrie. Les entités participant à une topologie demeurent des classes d'entités simples. Au lieu de modifier la définition de la classe d'entités, une topologie joue le rôle de description de la manière dont les entités peuvent être associées spatialement.
Pourquoi utiliser une topologie ?
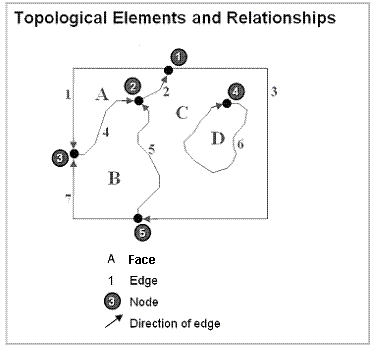
La topologie a longtemps été une exigence fondamentale SIG pour la gestion et l'intégrité des données. En général, un modèle de données topologique gère les relations spatiales en représentant les objets spatiaux (entités ponctuelles, linéaires et surfaciques) comme un graphique sous-jacent de primitives topologiques (nœuds, faces et limites). Ces primitives, combinées avec leurs relations mutuelles et leurs relations avec les entités dont elles représentent les limites, sont définies en représentant les géométries des entités dans un graphe planaire d'éléments topologiques.
La topologie est utilisée principalement pour garantir la qualité des données des relations spatiales et faciliter leur compilation. La topologie est également utilisée pour l'analyse des relations spatiales dans de nombreuses situations, telles que la fusion des limites entre polygones adjacents ayant des valeurs attributaires identiques ou le déplacement le long d'un réseau des éléments dans un graphe topologique.
La topologie permet également de modéliser la manière dont la géométrie de plusieurs classes d'entités peut être intégrée. Ceci est parfois appelé intégration verticale de classes d'entités.
Manières dont les entités partagent une géométrie dans une topologie
Des entités peuvent partager une géométrie dans une topologie. Voici quelques exemples concernant des entités adjacentes :
- Les entités surfaciques peuvent partager les limites (topologie de polygone).
- Les entités linéaires peuvent partager des extrémités (topologie limite-nœud).
En outre, une géométrie partagée peut être gérée entre des classes d'entités à l'aide d'une topologie de géodatabase, par exemple :
- Les entités linéaires peuvent partager des segments avec d'autres entités linéaires.
- Les entités surfaciques peuvent rencontrer d'autres entités surfaciques. Par exemple, des parcelles peuvent être incluses dans des îlots.
- Les entités linéaires peuvent partager des sommets d'extrémité avec d'autres points (topologie de nœud).
- Les entités ponctuelles peuvent rencontrer des entités linéaires (événements ponctuels).
Deux vues : entités et éléments topologiques
Une couche de polygones peut être décrite et utilisée des manières suivantes :
- Comme des ensembles d’entités géographiques (points, lignes et polygones)
- En tant que graphe d’éléments topologiques (nœuds, limites, faces et leurs relations)
Ceci signifie qu'il existe deux solutions pour utiliser des entités, une solution dans laquelle les entités sont définies par leurs coordonnées et un autre dans laquelle les entités sont représentées comme un graphe ordonné de leurs éléments topologiques.
Vous avez un commentaire à formuler concernant cette rubrique ?