Fonctionnement de l’attribution des pondérations via une comparaison par paires

L’outil Attribuer des pondérations via une comparaison par paires calcule les pondérations à partir d’une série de variables en entrée en vous permettant d’évaluer les variables par paires. Dans la boîte de dialogue de l’outil, les paires sont créées automatiquement à partir des variables en entrée. Chaque paire est associée à un curseur que vous pouvez ajuster pour indiquer quelle est la variable la plus importante et dans quelle mesure. Une matrice de comparaison est créée à partir des évaluations de comparaison par paires en fonction desquelles les pondérations sont calculées.

Les pondérations peuvent être utilisées dans un modèle d’adéquation dans Spatial Analyst qui utilise l’outil Somme pondérée, dans le modélisateur d’adéquation, ou dans un modélisateur d’adéquation construit dans Business Analyst. Les pondérations peuvent également être utilisées comme pondérations de variable dans l’outil Calculer l’indice composite dans les statistiques spatiales.

Comparaison par paires

Dans un modèle d’adéquation, la détermination des pondérations pour de nombreuses variables (ou critères) afin d’identifier leur importance relative est difficile et subjective. En revanche, la comparaison de paires de variables est plus précise. Par exemple, il peut être compliqué d’identifier les pondérations de cinq critères (pente, aspect, distance par rapport à l’eau, distance par rapport aux routes et élévation) les uns par rapport aux autres dans un modèle d’adéquation. Par contre, il est plus facile d’identifier lequel des critères, pente ou aspect, est le plus important et dans quelle mesure.

La méthode de comparaison par paires (Saaty 2008) est largement utilisée dans divers secteurs où l’approche multicritère pour la prise de décision est utilisée, comme la modélisation de l’habitat écologique, la sélection de sites d’entreprise et l’identification des indices de risque pour la santé. L’avantage de la pondération par paires est le suivant : en comparant deux éléments à la fois, elle simplifie les décisions complexes et fournit un moyen systématique de hiérarchiser ou de classer les variables en entrée. Étant donné que vous pouvez comparer plus précisément les paires de variables les unes par rapport aux autres, les pondérations finales calculées sont plus objectives. Pour vérifier que les comparaisons par paires sont cohérentes (par exemple, si A > B et B > C, C ne peut pas être supérieur à A), l’outil met à disposition une fonctionnalité de diagnostic.

Exemples d’application

Voici des exemples d’application de la comparaison par paires :

• Calculer les pondérations pour plusieurs critères dans un modèle d’adéquation.
• Déterminer les pondérations pour un ensemble de sous-modèles pour un modèle d’adéquation composite.
• Évaluer l’importance relative de différents types d’utilisation du sol dans une couche.
• Calculer les pondérations relatives de différents polluants pour créer un indice de qualité de l’air afin d’influencer l’action publique.
• Identifier de nouvelles valeurs de classe lors de la reclassification d’une couche raster en fonction des préférences.
• Estimer les priorités relatives pour plusieurs projets dans une prise de décision d’entreprise.

Méthodologie de comparaison par paires

Développée par Thomas L. Saaty (Saaty 2008), la comparaison par paires fournit une structure permettant de dériver des pondérations d’importance relatives pour plusieurs variables. Au lieu de classer simultanément toutes les variables, les comparaisons par paires fournissent une méthode structurée pour évaluer l’importance des variables en les comparant par paires. Cette approche est particulièrement utile si vous traitez des facteurs intangibles qui ne peuvent pas être mesurés directement, mais qui sont essentiels à la prise de décision. Cette méthode s’appuie sur des jugements d’experts afin d’établir des échelles de priorité qui mesurent les facteurs en termes relatifs.

Processus de comparaison par paires

Voici les principales étapes du processus de comparaison par paires :

1. Identifiez les variables à comparer.
2. Spécifiez les comparaisons pour les paires de variables et créez une matrice de comparaison.
3. Calculez les pondérations à partir de la matrice de comparaison et générez une table en sortie.

L’outil Attribuer des pondérations via une comparaison par paires crée dynamiquement des paires à partir des variables en entrée. Utilisez les curseurs afin d’identifier pour chaque paire quelles sont les variables les plus importantes et dans quelle mesure. Au fur et à mesure des comparaisons, la matrice de comparaison est mise à jour. Les pondérations finales sont déterminées à partir de la matrice de comparaison.

La sortie de l’outil est un ensemble de pondérations dérivées pour les variables en entrée avec ou sans matrice de comparaison.

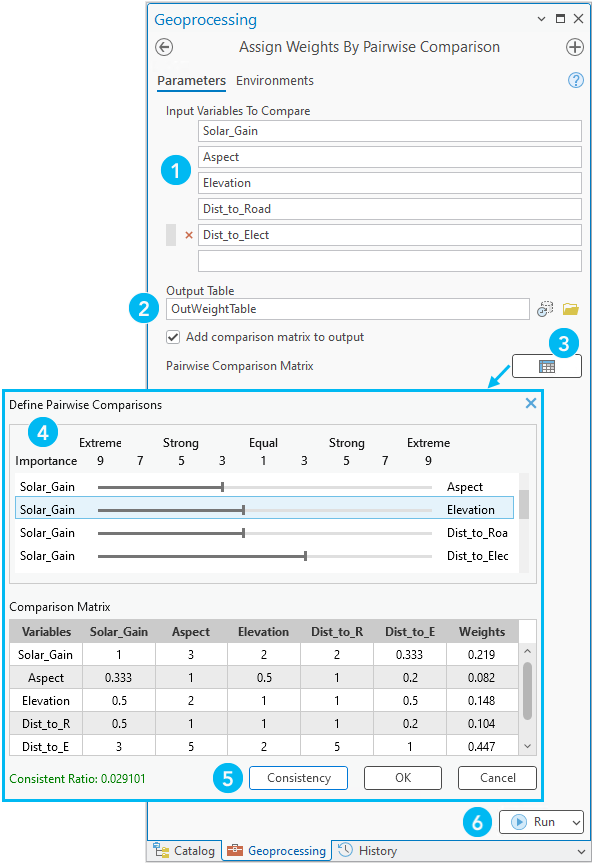
Utiliser l’outil pour attribuer des pondérations via une comparaison par paires

Voici un processus courant utilisant l’outil. Les numéros d’étape ci-dessous correspondent aux numéros figurant dans l’image ci-dessus.

1. Indiquez les noms des variables à comparer dans le paramètre Variables en entrée à comparer.
2. Si vous le souhaitez, changez la valeur du paramètre Table en sortie générée automatiquement.
3. Pour le paramètre Matrice de comparaison par paires, cliquez sur le bouton Comparer les variables et calculer les pondérations.

   La fenêtre Définir des comparaisons par paires, qui contient la table Matrice de comparaison, s’ouvre.

4. Spécifiez les comparaisons par paires en déplaçant les curseurs pour chaque paire.
5. Cliquez sur Cohérence pour vérifier que les comparaisons par paires sont cohérentes.
6. Cliquez sur Exécuter.

L’outil utilise une échelle de 1 à 9 développée par Saaty (2008). L’échelle, les définitions et les explications de chaque valeur sur l’échelle sont présentées dans le tableau ci-dessous.

Intensité de l’importance	Définition	Explication
1	Importance égale	Deux activités contribuent de façon égale à l’objectif.
2	Faible ou légère
3	Importance modérée	L’expérience et le jugement favorisent légèrement une activité par rapport à l’autre.
4	Modérée plus
5	Importance forte	L’expérience et le jugement favorisent fortement une activité par rapport à l’autre.
6	Forte plus
7	Importance très forte ou démontrée	Une activité est favorisée très fortement par rapport à une autre. Sa dominance est démontrée dans la pratique.
8	Très très forte
9	Importance extrême	L’indice favorisant une activité par rapport à l’autre est une affirmation du niveau le plus élevé possible.

Matrice de comparaison

La matrice de comparaison est au cœur de la méthodologie de comparaison par paires. Elle est remplie avec les préférences de paires à partir desquelles les pondérations sont calculées.

Dans la matrice, l’intersection de chaque ligne avec chaque colonne représente une paire de variables à comparer. Dans la boîte de dialogue, pour chaque paire, ajustez le curseur afin d’indiquer votre préférence de comparaison. Si vous déplacez le curseur d’un côté, vous indiquez une préférence plus forte pour cette variable. Si vous conservez le curseur au centre, cela signifie que les variables ont la même importance. Ce processus implique des jugements subjectifs en fonction de vos connaissances, de votre expérience ou de vos préférences.

La matrice de comparaison est mise à jour à mesure que les curseurs sont déplacés. L’outil attribue les valeurs sélectionnées des curseurs à la cellule située à l’intersection de la ligne (la variable la plus importante) et de la colonne (la variable la moins importante) correspondantes. Sa valeur réciproque (1/valeur) est attribuée à la position opposée dans la matrice.

Par exemple, si vous évaluez les variables Solar_Gain et Elevation dans un modèle d’adéquation de parc solaire, vous pouvez considérer que la variable Solar_Gain est deux fois plus importante que la variable Elevation. Pour refléter cette évaluation, déplacez le curseur pour les deux variables du côté de Solar_Gain, entre 1 et 3 sur l’échelle. Dans la matrice de comparaison, la valeur de la cellule située à l’intersection de la ligne Solar_Gain et la colonne Elevation est mise à jour avec 2 et la valeur réciproque (1/2 ou 0,5) est attribuée automatiquement à la cellule située à l’intersection de la ligne Elevation et de la colonne Solar_Gain.

Calculs pour la comparaison par paires

Le calcul des pondérations à partir d’une matrice de comparaison est un traitement à plusieurs étapes, comme illustré dans l’image ci-dessous :

Cette image illustre les étapes permettant de calculer les pondérations à partir d’une matrice de comparaison.

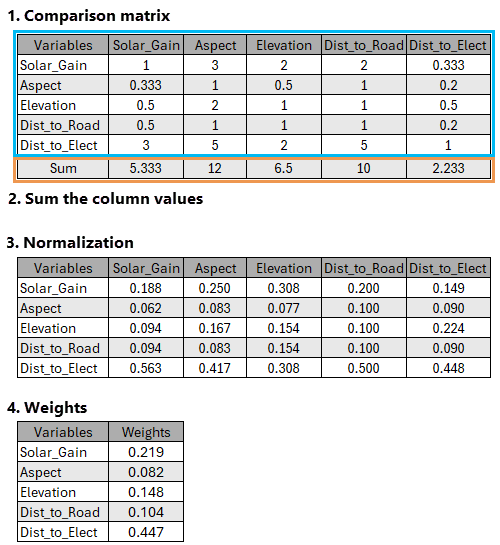
Les quatre étapes sont décrites ci-dessous.

Matrice de comparaison

Créez la matrice de comparaison identifiant les évaluations de comparaison par paires pour les variables en entrée.

Additionner les colonnes

L’outil additionne les valeurs des cellules pour chaque colonne.

Le total obtenu pour la colonne est utilisé pour normaliser les valeurs dans cette colonne. Dans l’exemple de comparaison par paires de l’image ci-dessus, la première colonne, Solar_Gain, contient les valeurs, 1, 0,333, 0,5, 0,5, et 3, dont le total est 5,333.

Le total de 5,333 sera utilisé pour normaliser chaque valeur dans la première colonne et est utilisé à l’étape suivante.

Normaliser

Chaque valeur normalisée pour chaque paire de comparaison est calculée en divisant la valeur de comparaison correspondante par le total de sa colonne.

Par exemple, la valeur normalisée pour la cellule située à l’intersection de la ligne Solar_Gain et de la colonne Solar_Gain est 1/5,333 ≈ 0,188

Calculer les pondérations

Pour calculer la pondération finale de chaque variable, la moyenne de toutes les cellules normalisées sur chaque ligne est déterminée.

Pour la première ligne dans la matrice Table de normalisation dans l’image ci-dessus, le calcul est le suivant :

Ce calcul est effectué pour toutes les variables afin de déterminer leurs pondérations.

Ajuster le ratio de cohérence

Cliquez sur Cohérence pour vérifier la cohérence entre les comparaisons de toutes les paires. Le ratio de cohérence est affiché au bas du tableau. Si le ratio est supérieur à 0,1, les comparaisons ne sont pas cohérentes. Le ratio est affiché en rouge, comme les trois paires les plus incohérentes (voir l’exemple ci-dessous). Vous pouvez ajuster les comparaisons incohérentes à l’aide des curseurs pour garantir la cohérence.

Reportez-vous à la rubrique Calculer le ratio de cohérence pour des détails sur la façon de déterminer le ratio de cohérence.

Formats de matrice de comparaison en entrée

Voici des exemples de formats valides pouvant être utilisés comme valeur du paramètre comparison_matrix sans et avec pondérations.

Sans pondérations

Voici un exemple de matrice de comparaison en entrée au format de table sans pondérations :

Variables	Dist_Roads	Elevation	Landuse	Aspect
Dist_Roads	1	0,333	3	1
Elevation	3	1	0,2	3
Landuse	0,333	5	1	7
Aspect	1	0,333	0,143	1

Il existe deux formats de texte pour la matrice de comparaison en entrée sans pondérations.

Le premier format répertorie les variables et leurs évaluations dans un tableau avec texte. Exemple :

Variables, Dist_Roads, Elevation, Landuse, Aspect Dist_Roads,1,0,333,3,1 Elevation,3,1,0,2,3 Landuse,0,333,5,1,7 Aspect,1,0,333,0,143,1

Le deuxième format répertorie chacune des paires de variables et leurs évaluations. Exemple :

Variables Dist_Roads Elevation 0,333; Dist_Roads Landuse 3; Dist_Roads Aspect 1; Elevation Landuse 0,2; Elevation Aspect 3; Landuse Aspect 7;

Avec pondérations

Voici un exemple de matrice de comparaison en entrée au format de table avec pondérations :

Variable	Dist_Roads	Elevation	Landuse	Aspect	Pondérations
Dist_Roads	1	0,333	3	1	0,253
Elevation	3	1	0,2	3	0,252
Landuse	0,333	5	1	7	0,407
Aspect	1	0,333	0,143	1	0,088

Remarque :

Si les pondérations ont déjà été calculées, il n’est pas vraiment nécessaire d’utiliser l’outil pour les recalculer. Si les pondérations sont incluses dans la valeur du paramètre comparison_matrix, elles sont ignorées et recalculées par l’outil. Les pondérations sont incluses dans la matrice, dans certains cas, lorsque la matrice de comparaison provient d’un autre outil ou d’une autre application.

Deux formats de texte sont admis pour la matrice de comparaison en entrée avec pondérations.

Le premier format répertorie les variables et leurs évaluations et pondérations dans un tableau avec texte. Exemple :

Variables, Dist_Roads, Elevation, Landuse, Aspect, Weights Dist_Roads,1,0,333,3,1,0,253 Elevation,3,1,0,2,3,0,252 Landuse,0,333,5,1,7,0,407 Aspect,1,0,333,0,143,1,0,088

Le deuxième format est divisé en deux sections. La première section identifie les variables en répertoriant toutes les paires de variables et leurs évaluations. Dans la deuxième section, les variables sont spécifiées avec leur pondération finale. Exemple :

Variables Dist_Roads Elevation 0,333; Dist_Roads Landuse 3; Dist_Roads Aspect 1; Elevation Landuse 0,2; Elevation Aspect 3; Landuse Aspect 7; Weights Dist_Roads 0,252906; Elevation 0,252138; Landuse 0,406524; Aspect 0,088432;

Matrice de comparaison Python

Entrez directement les paires et leurs évaluations en tant que valeur du paramètre comparison_matrix dans Python comme suit :

Variables Dist_Roads Elevation 0.333; Dist_Roads Landuse 3; Dist_Roads Aspect 1; Elevation Landuse 0.2; Elevation Aspect 3; Landuse Aspect 7;

Remarque :

L’ordre des comparaisons par paires dans les formats de table ou de fichier texte ou fourni comme valeur du paramètre comparison_matrix dans Python doit être le même que celui indiqué par la valeur du paramètre input_variables. Lorsque l’ordre est indiqué au format de fichier texte d’appariement des variables ou fourni directement dans le paramètre, les appariements et leurs évaluations doivent répertorier la première variable appariée séquentiellement avec chacune des autres variables. Ensuite, la deuxième variable est appariée séquentiellement avec les autres variables, etc.

Formats de table en sortie

Voici des exemples de tables en sortie de l’outil avec et sans la matrice de comparaison.

Avec la matrice de comparaison

Le tableau suivant inclut la matrice de comparaison lorsque le paramètre Inclure la matrice de comparaison dans la sortie est sélectionné :

Matrice de comparaison et pondérations associées

Variable	Dist_Roads	Elevation	Landuse	Aspect	Pondérations
Dist_Roads	1	0,333	3	1	0,253
Elevation	3	1	0,2	3	0,252
Landuse	0,333	5	1	7	0,407
Aspect	1	0,333	0,143	1	0,088

Voici un exemple de table en sortie lorsque le paramètre Inclure la matrice de comparaison dans la sortie est sélectionné et que la sortie est de type texte :

Variables, Dist_Roads, Elevation, Landuse, Aspect, Weights Dist_Roads,1,0,333,3,1,0,253 Elevation,3,1,0,2,3,0,252 Landuse,0,333,5,1,7,0,407 Aspect,1,0,333,0,143,1,0,088

Avec pondérations uniquement

Les formats suivants sont utilisés lorsque le paramètre Inclure la matrice de comparaison dans la sortie n’est pas sélectionné.

Lorsque le type de sortie spécifié est table, la table en sortie contient deux colonnes : Variables et Weights.

Variables	Pondérations
Dist_Roads	0,253
Elevation	0,252
Landuse	0,407
Aspect	0,088

Lorsque la sortie est de type texte, la table est un fichier texte structuré contenant les pondérations dérivées pour chaque variable en fonction des comparaisons par paires. Exemple :

Variables, Weights Dist_Roads,0,253 Elevation,0,252 Landuse,0,407 Aspect,0,088

Bibliographie

Saaty, T. L. 2008. "Decision making with the analytic hierarchy process". International Journal of Services Sciences, 1(1), 83-98.