[予備回帰分析 (Exploratory Regression)] ツールを実行したときの一次出力はレポートです。このレポートは、ツールの実行中にメッセージとして作成され、プロジェクトのジオプロセシング履歴からアクセスできます。必要に応じて、テストされたモデルをさらに調査するのに役立つテーブルも作成されます。レポートの目的の 1 つは、候補として検討する説明変数から、適切に指定された OLS モデルが得られるどうかを確認することです。ただし、適合モデル ([予備回帰分析 (Exploratory Regression)] ツールを起動したときに指定した基準のすべてを満たすモデル) がない場合、出力には、どの変数が整合性のある予測子であるかが示され、どの診断に問題があるかを判断することができます。各診断に関連する問題への対処方法は、「回帰分析の基礎」 (「一般的な回帰分析の問題、結果、対策」を参照) と「回帰分析の詳細」に記載されています。適切に指定された OLS モデルがあるかどうかを判断する方法の詳細については、「回帰分析の基礎」と「最小二乗法 (Ordinary Least Squares) ツールの結果の解析」をご参照ください。
レポート
[予備回帰分析 (Exploratory Regression)] のレポートには、5 つのセクションがあります。それぞれのセクションについて説明します。
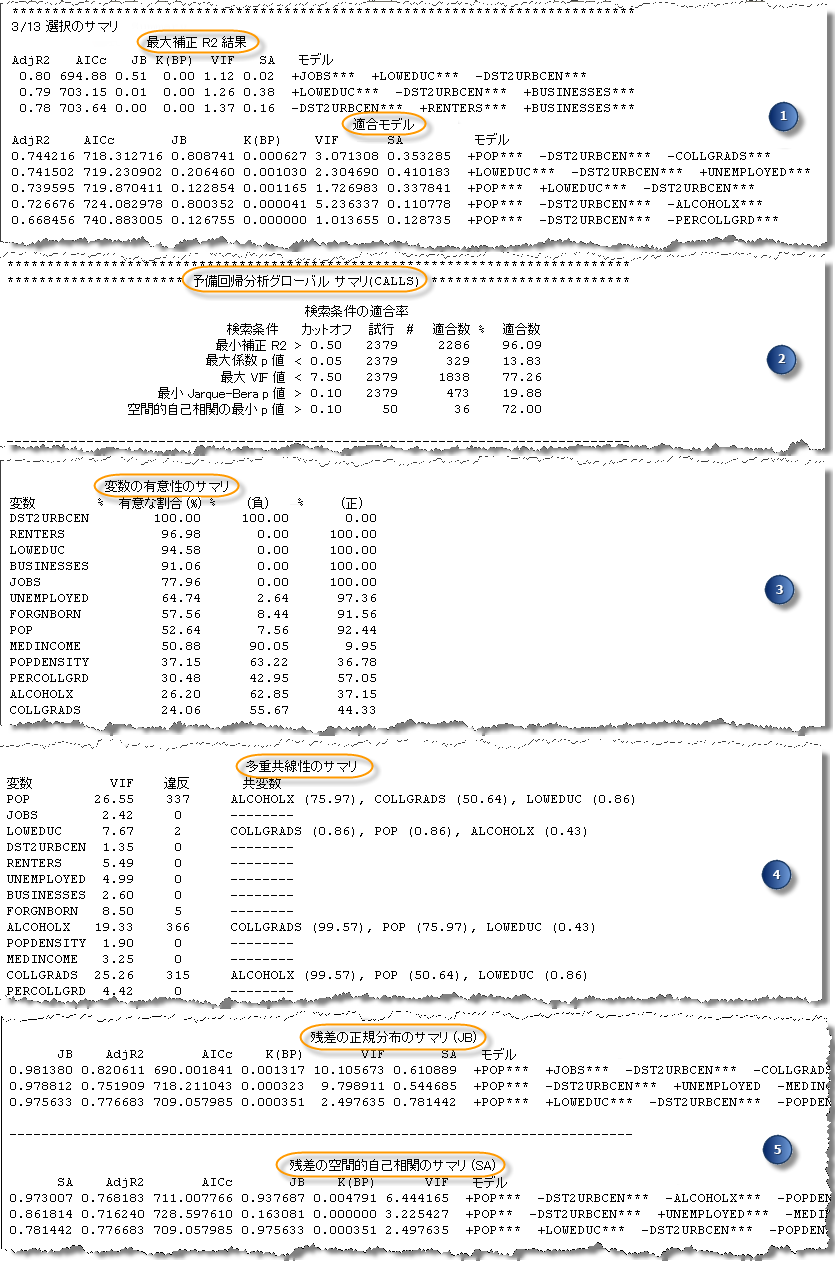
1. 説明変数の数による最適なモデル

出力レポートの最初のサマリーは、テストされたモデルの説明変数の数でグループ化されます。[説明変数の最小数] パラメーターに 1 を指定し、[説明変数の最大数] パラメーターに 5 を指定すると、サマリー セクションは 5 つになります。各セクションには、最大補正 R2 値を持つ 3 つのモデルとすべての適合モデルが表示されます。各サマリー セクションには、以下に表示する各モデルの診断値も含まれます。補正赤池情報量基準 - AICc、Jarque-Bera p 値 - JB、Koenker スチューデント化 Breusch-Pagan p 値 - K (BP)、最大分散拡大係数 - VIF、残差の空間的自己相関分析の計測値 (Global Moran’s I p 値) - SA これらのサマリーにより、モデルの予測の適切さ (補正 R2) と、指定した診断基準のすべてを満たすモデルがわかります。デフォルトの検索基準 ([最小許容補正 R2]、[最大係数 p 値カットオフ]、[最大 VIF 値カットオフ]、[最小許容 Jarque Bera p 値]、[空間的自己相関の最小許容 p 値] の各パラメーター) をすべて受け入れた場合、適合モデル リストに含まれるモデルはすべて、適切に指定された OLS モデルとなります。
適合モデルがない場合でも、出力レポートの他の部分に変数のリレーションシップに関する有益な情報が数多くあるため、これを利用して対応方法を決定できます。
2. 予備回帰分析グローバル サマリー
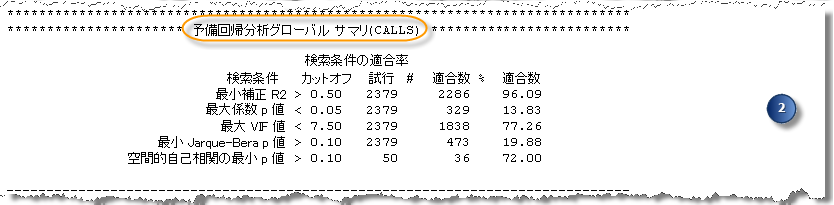
「予備回帰分析グローバル サマリー」セクションには、適合するモデルが見つからなかった理由が示されるため、特に適合モデルが見つからない場合はこのセクションから確認することが重要です。このセクションには、5 つの診断テストと、これらの各テストに適合したモデルの割合 (%) が表示されます。適合モデルがない場合、このサマリーを見ると、どの診断テストに問題があるのかがわかります。
多くの場合、問題のある診断テストは、空間的自己相関分析 (SA) の Global Moran’s I テストです。テストされたモデルのすべてに空間的自己相関回帰残差がある場合、多くは、重要な説明変数がないことを示します。足りない説明変数を見つける最善の方法の 1 つは、[最小二乗法 (Ordinary Least Squares)] (OLS) ツールによる残差出力のマップを調べることです。残りのすべての基準を満たす予備回帰分析モデルのいずれかを選択 (最大補正 R 2 値のリストを使用するか、オプションの出力テーブルの中からモデルを選択) し、そのモデルを使用して OLS を実行します。[最小二乗法 (Ordinary Least Squares)] (OLS) ツールから、モデルの残差のマップが出力されます。残差を調べて、足りない変数を見つけるヒントがないか確認します。できるだけ多くの候補となる説明変数を考えます (たとえば、主要な高速道路、病院、またはその他の重要な地理フィーチャまでの距離など)。空間様式変数を試すことを検討します。たとえば、下方予測のすべてが農村部にある場合、ダミー変数を作成して、[予備回帰分析 (Exploratory Regression)] ツールの結果が改善するかどうか確認します。
一般に問題となりやすい他の診断テストは、正規分布している残差を求める Jarque-Bera 検定です。モデルのいずれもが Jarque-Bera (JB) 検定に適合しない場合、モデルの偏りに問題があります。モデルの偏りの一般的な原因には、次のようなものがあります。
- 非線形リレーションシップ
- データの外れ値
独立変数と相対関係にある候補となる説明変数の散布図マトリックスを表示すると、どちらの問題かがわかります。詳細については、「回帰分析の基礎」をご参照ください。モデルが空間的自己相関分析テスト (SA) に適合しない場合、まずこれらの問題を修正します。偏りは、重要な説明変数がないために起こることがあります。
3. 変数の有意性のサマリー
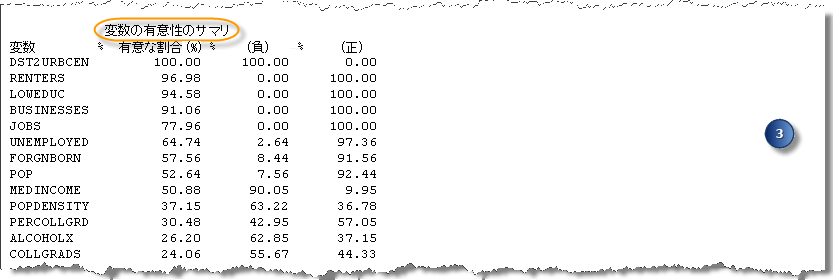
「変数の有意性のサマリー」セクションには、変数のリレーションシップに関する情報と、これらのリレーションシップの一貫性についての説明があります。候補となるそれぞれの説明変数は、それが統計的に有意だった割合とともに表示されます。リスト内の最初にある複数の変数が最大値を持ち、有意な割合 (%)列として表示されています。% (負) 列と % (正) 列を調べることによって、変数のリレーションシップの安定性を確認することもできます。強力な予測子は常に有意となり ([有意な割合 (%)])、リレーションシップは安定します (主に負または主に正)。
レポートのこの部分は、効率の向上にも役立ちます。(50 を超える) 数多くの候補となる説明変数を扱って、5 つ以上の予測子を持つモデルを扱おうとする場合に特に重要です。数多くの説明変数を持ち、多くの組み合わせをテストする場合、計算に時間がかかることがあります。実際に、メモリ エラーにより作業が完了できない場合もあります。以下のように、テストするモデルの数を徐々に増やすのがよい方法です。[説明変数の最小数] と [説明変数の最大数] の両方の値を 2、3、4 と徐々に増やして設定していきます。それぞれを実行して、テストしたモデルの統計的な有意性が低い変数を削除します。「変数の有意性のサマリー」セクションは、常に強力な予測子である変数を見つけるのに役立ちます。リストから候補となる説明変数を 1 つ削除するだけで、[予備回帰分析 (Exploratory Regression)] ツールの作業時間が大きく短縮される可能性があります。
4. 多重共線性のサマリー
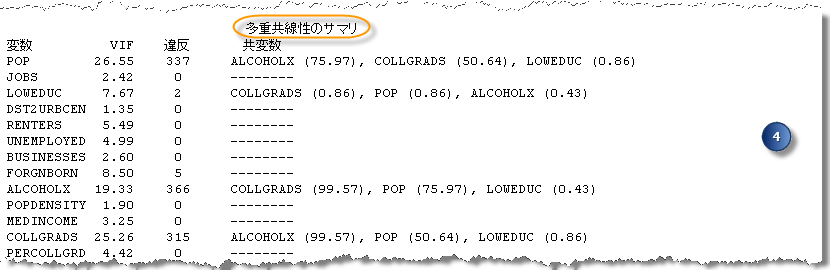
このレポートの「多重共線性のサマリー」セクションと「変数の有意性のサマリー」セクションを利用すると、パフォーマンスを改善するために、どの候補となる説明変数を分析から削除できるかがわかります。「多重共線性のサマリー」セクションでは、それぞれの説明変数が多重共線性の高いモデルに含まれていた回数と、これらのモデルに含まれていたその他の説明変数がわかります。多重共線性の高いモデルで、2 つ (またはそれ以上) の説明変数が頻繁に一緒に見つかる場合、これらの変数は同じストーリーを示している可能性があることを示しています。独立変数の固有の側面を説明する変数だけを含めるために、重複する変数から今後の分析に含めるものを 1 つ選択します。「変数の有意性のサマリー」に基づいて、重複する変数から最強のものを使用するという方法があります。
5. その他の診断サマリー

最後の診断サマリーには、最大 Jarque-Bera p 値 (残差の正規分布のサマリー) と最大 Global Moran’s I p 値 (残差の空間的自己相関のサマリー) が表示されます。これらの診断テストに適合するには、p 値を大きくしなければなりません。
モデルが Jarque-Bera と空間的自己相関分析 (Global Moran’s I) テストに適合している場合には、特にこれらのサマリーは役に立ちません。それは、統計的有意性の基準が 0.1 の場合、0.1 より大きな値を持つモデルはすべて適合モデルになるためです。ただし、適合モデルがなく、正規分布している残差または統計的に有意な空間的自己相関がない残差があるのかないのかを知りたい場合には、これらのサマリーは有益です。たとえば、Jarque-Bera サマリーの p 値のすべてが 0.000000 である場合、正規分布している残差はまったくないことが明らかです。一方、p 値が 0.092 である場合は、正規分布している残差があるといってもよいでしょう (実際、選択した有意性のレベルによって、0.092 の p 値は適合する可能性があります)。これらのサマリーは問題の重要度を示し、どのモデルも適合しない場合に、どの変数が少なくとも適合に近いモデルに関連付けられているかを示します。
テーブル
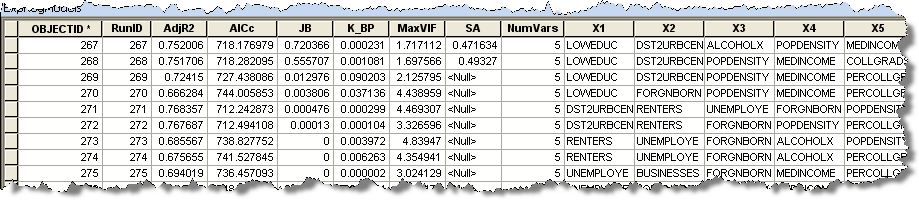
[出力結果テーブル] に値を入力した場合、[最大係数 p 値カットオフ] と [最大 VIF 値カットオフ] の基準を満たしたすべてのモデルを含むテーブルが作成されます。適合モデルがない場合でも、出力テーブルにモデルが表示される可能性があります。テーブルの各行は、係数と VIF 値の基準を満たすモデルを表します。テーブルの列には、モデル診断と説明変数があります。表示されている診断は、補正 R2、補正赤池情報量基準 (AICc)、Jarque-Bera p 値 (JB)、Koenker スチューデント化 Breusch-Pagan p 値 (BP)、分散拡大係数 (VIF)、Global Moran’s I p 値 (SA) です。AICc 値によってモデルを分類できます。AICc 値が低いほど、モデルのパフォーマンスは向上します。ArcMap の AICc 値を分類するには、AICc 列をダブルクリックします。(残差を調べるために) OLS 分析で使用するモデルを選択する場合、低い AICc 値とできる限り多くの他の診断に適合する値を持つモデルを選択してください。たとえば、出力レポートを見て、Jarque-Bera の診断に問題があることがわかった場合、Jarque-Bera 以外の基準をすべて満たす、最小 AICc 値を持つモデルを探します。
参考資料
ArcGIS の回帰分析の初心者には、「無料の Esri バーチャル キャンパスの回帰に関するトレーニング セミナー」をご覧になり、「回帰分析に関するチュートリアル」を学習してから、[予備回帰分析 (Exploratory Regression)] を使用することを強くお勧めします。
以下もご参照ください。
- [予備回帰分析 (Exploratory Regression)] の詳細
- 回帰分析の側面
- 回帰分析の基礎
Burnham, K.P. and D.R. Anderson. 2002. Model Selection and Multimodel Inference: a practical information-theoretic approach, 2nd Edition New York: Springer. Section 1.5