陰影起伏 (Hillshade) の仕組み—ArcGIS Pro

Spatial Analyst のライセンスで利用可能。

3D Analyst のライセンスで利用可能。

[陰影起伏 (HillShade)] ツールは、ラスター内の各セルについてイルミネーション値を決定することにより、サーフェスの仮想的なイルミネーションを求めます。これは、仮想光源の位置を設定し、各セルのイルミネーション値を隣接セルに対して計算することにより行います。これにより、解析や視覚的表示、特に透過表示を使用する場合に、サーフェスの視覚化が大幅に向上します。

デフォルトでは、影と光はグレーの階調で 0 (黒) ～ 255 (白) の整数が関連付けられています。

陰影起伏のパラメーター

特定の場所の陰影起伏マップを作成する際に最も重要なのは、天空での太陽の位置です。

方位

方位は太陽の方位角方向で、北から右回りに 0 ～ 360 度で計測されます。方位 90 度は東です。デフォルトの方位は 315 度 (北西) です。

高度

高度は、水平線を基準とする光源の傾斜角です。単位は角度で、範囲は 0 (水平線上) ～ 90 度 (真上) です。デフォルト値は 45 度です。

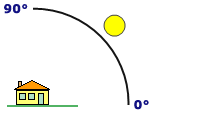
陰影起伏の例

次の陰影起伏例では、方位 315 度、高度 45 度に設定されています。

マップ表示での陰影起伏の使用

標高ラスターの[表示設定] タブの [レイヤーの透過表示] スライダーを使用することで、視覚効果の高い立体的な地形図を簡単に作成できます。

透過表示を使用して、標高ラスターと陰影起伏を結合 — 標高ラスターと陰影起伏ラスターを組み合わせ、透過率を設定することで、陰影起伏ラスターを作成

土地利用タイプ、植生、道路、河川など他のレイヤーを追加すれば、さらに詳しい情報をマップに表示できます。

解析での陰影起伏の使用

陰影をモデル化することにより (デフォルトのオプション)、局所のイルミネーションを計算して、セルが陰影内にあるかどうかを調べることができます。

陰影をモデル化することにより、1 日の特定の時間に別のセルの影になるセルを特定できます。別のセルの影が掛かるセルは、0 にコード化されます。その他のセルは 1 ～ 255 の整数でコード化されます。1 より大きい値をすべて 1 に再分類して、バイナリ出力ラスターを作成できます。次の例では、黒のエリアが影です。各画像で光源方位は同じですが、太陽の角度 (高度) が変更されています。

陰影起伏の計算方法

陰影値を計算するには、まず、光源の高度と方位を指定する必要があります。傾斜角度および傾斜方向の計算でこれらの値が処理され、出力ラスターの各セルの最終的な陰影起伏値が決定されます。

陰影起伏アルゴリズム

陰影起伏値を計算するためのアルゴリズムは次のとおりです。

(1)  陰影起伏 = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) +
                 (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))

陰影起伏の計算値が 0 より小さい場合、出力セル値は 0 になります。

光源角度の計算

光源の高さは、水平を基準とする角度で指定されます。ただし、陰影起伏値を求める数式では、角度の単位がラジアンであり、天頂からの偏向を表している必要があります。サーフェスから真上の方向 (頭上) が天頂になります。天頂角は、天頂点から光源方向に測定され、高度の余角となります。光源角度を計算するには、まず、高度を天頂角に変換します。次に、その角度をラジアンに変換します。

高度 (Altitude) を天頂角 (Zenith_deg) に変換するには:

(2)  Zenith_deg = 90 - 高度

ラジアン単位 (Azimuth_rad) に変換するには:

(3)  Zenith_rad = Zenith_deg * pi / 180.0

光源方向の計算

光源の方向 (方位) は「度」で表されます。陰影起伏の数式では、この角度がラジアン単位で表されている必要があります。まず、方位角を地理単位 (コンパス方位) から数学単位 (直角) に変換します。次に、方位角の単位をラジアンに変換します。

方位角の測定方式を変換するには:

(4)  Azimuth_math = 360.0 - 方位角 + 90

Azimuth_math >= 360.0 の場合:

(5)  Azimuth_math = Azimuth_math - 360.0

ラジアン単位 (Azimuth_rad) に変換するには:

(6)  Azimuth_rad = Azimuth_math * pi / 180.0

傾斜角と傾斜方向の計算

3 x 3 ウィンドウが入力ラスターの各セルへ移動し、このウィンドウの中心に位置するセルと、それに隣接する 8 つのセルの値に基づいて、傾斜角と傾斜方向が計算されます。これらのセルは a ～ i の文字で識別され、傾斜方向の計算対象となるセルには e が割り当てられます。

セル e の X 方向の変化率は、次のアルゴリズムで計算されます。

(7)  [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * セル サイズ)

セル e の Y 方向の変化率は、次のアルゴリズムで計算します。

(8)  [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * セル サイズ)

サーフェス内の各セルからの最も急な下り坂が傾斜です。ラジアン単位の傾斜角 (Slope_rad) を求めるアルゴリズムは次のとおりです。ここでは Z 係数を使用します。

(9)  Slope_rad = ATAN (z_factor * √ ([dz/dx]² + [dz/dy]²))

最も急な下り坂が面している方向が傾斜方向です。ラジアン単位の傾斜方向は 0 ～ 2pi の範囲で定義され、0 は東向きになります。傾斜方向は、次のアルゴリズムの規則に基づいて決定されます。

(10)  If [dz/dx] is non-zero:
    Aspect_rad = atan2 ([dz/dy], -[dz/dx])      if Aspect_rad < 0 then        Aspect_rad = 2 * pi + Aspect_rad  If [dz/dx] is zero:
    if [dz/dy] > 0 then      Aspect_rad = pi / 2    else if [dz/dy] < 0 then      Aspect_rad = 2 * pi - pi / 2    else      Aspect_rad = Aspect_rad

陰影起伏の計算例

例として、移動ウィンドの中央セルの陰影起伏値を計算します。

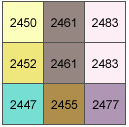
セルサイズは 5 単位です。デフォルトの Altitude (高度) 45 度と Azimuth (光源方位) 315 度を使用します。

イルミネーション角度

数式 2 により点頂角 (Zenith_deg) を求める:

(2)  Zenith_deg = 90 - 高度                = 90 - 45                = 45

数式 3 により、ラジアン (Zenith_rad) に変換:

(3)  Zenith_rad = Zenith_deg * pi / 180.0                = 45 * 3.1428571429 / 180                = 0.7857142857

イルミネーション方向

数式 4 により、方位角を地理角度から数学的角度 (Azimuth_math) に変換:

(4)  Azimuth_math = 360.0 - 方位 + 90                = 360.0 - 315 + 90                = 135                = 2.3571428571

数式 6 により、方位角をラジアン (Azimuth_rad) に変換:

(6)  Azimuth_rad = Azimuth_math * pi / 180.0                = 135 * 3.1438571429 / 180

傾斜角と傾斜方向

セル e について、X 方向の変化率を求める:

(7)  [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * セル サイズ)             = ((2483 + 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5)             = (9926 - 9801)/ 40             = 3.125

セル e について、Y 方向の変化率を求める:

(8)  [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize)             = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5)             = (9834 - 9855) / 40             = -0.525

傾斜角 (Slope_rad) を求める:

(9)  Slope_rad = ATAN ( z_factor * √ ([dz/dx]² + [dz/dy]²))               = atan(1 * sqrt(3.125 * 3.125 + -0.525 * -0.525))               = 1.26511

この例では dz/dx がゼロではないので、規則 10 に基づいて傾斜方向 (Aspect_rad) を求める:

  Aspect_rad = atan2 ([dz/dy], -[dz/dx])             = atan2(-0.525, -3.125)             = -2.9751469600412

この値は 0 より小さいので、これに相当する規則を適用する:

  Aspect_rad = 2 * pi + Aspect_rad             = 2 * 3.1428571429 + -2.9751469600412             = 3.310567

陰影起伏

最終的な陰影起伏 (Hillshade) を計算する:

Hillshade = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) +              (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))
          = 255.0 * ((cos(0.7857142857) * cos(1.26511)) +
             (sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567)))
          = 153.82

出力ラスターは整数型なので、中央セル e の陰影値は「154」になります。

参照

Burrough, P. A. and McDonell, R. A., 1998. 『Principles of Geographical Information Systems』 (Oxford University Press, New York), 190 pp.