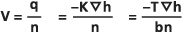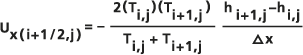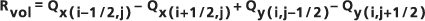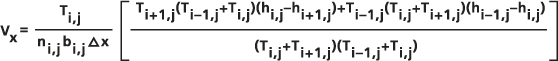Spatial Analyst のライセンスで利用可能。
[ダルシー フロー (Darcy Flow)] および [ダルシー流速 (Darcy Velocity)] を [粒子追跡 (Particle Track)] および [多孔質媒体内の分散 (Porous Puff)] とともに使用して、地下水成分の基本的な移流拡散モデリングを実行することができます。この方法では、2 次元の、垂直方向に混合された、水平の、水頭が深さに依存しない、安定状態のフローをモデル化します。
ダルシー フローの計算
ダルシー フローの計算に使用する式について、以降のセクションで詳細に説明します。
フローと流速の計算
ダルシーの法則は、多孔質媒体における ダルシー流速 q は、透水係数 K と水頭勾配
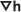 (等方性の帯水層で流れ方向の単位長さにおける水頭の変化量) により次式で計算されることを示します。
(等方性の帯水層で流れ方向の単位長さにおける水頭の変化量) により次式で計算されることを示します。- q = -K
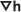
K は、透水率 T と層厚 b から次式で計算できます。K = T/b
この q(単位: 体積/時間/面積) は、比流量、体積流束、または濾過速度とも呼ばれます。Bear (1979) は、q を、流れの方向に垂直な単位断面積を単位時間に流れる水の体積として定義しました。
- q = -K
この体積流速に密接に関連するのは帯水層流束 U で、これは帯水層の単位幅あたりの流量です (単位は体積/時間/長さ)。
- U = -T
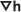
この式は、水頭が深さに依存せず、流れが水平方向であることを前提にしています。
- U = -T
間隙内の平均流速は浸透流速 V と呼ばれ、ダルシー流速を媒体の有効間隙率で除算したものです。
ダルシー フロー の実行では、この浸透流速 V がセル単位で計算されます。セル i,j について、セルの 4 つの壁から、隣接する 2 つのセルの水頭差、および透水率 Ti+1/2,j の調和平均 (Konikow と Bredehoeft、1978) (等方性と仮定) を使用して、帯水層流束 U が計算されます。
たとえば、
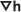 の x コンポーネントについて、セル i,j および i+1,j の式は次のとおりになります。
の x コンポーネントについて、セル i,j および i+1,j の式は次のとおりになります。- δh/δx ≈ (hi+1 - hi) / Δx
以下の図に、この方法を示します。
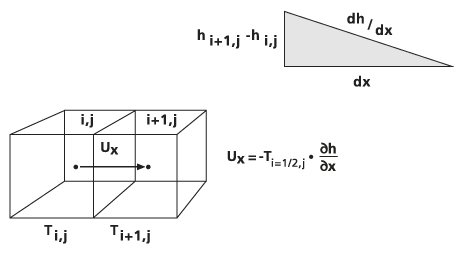
残余水量の計算
以下のセルの壁の計算では、セル i,j とセル i+1,j の間の帯水層流束は X 方向に平行に流れ、次式で計算されます。
地下水量収支を求めるには、セルの壁から流出する地下水流量を計算する必要があります。この流量 Qx(i+1/2) は、帯水層流束 U とセルの壁の幅 Δy を使用して次式で計算されます。
- Qx(i+1/2,j) = Ux(i+1/2,j) Δy
セルの 4 つの壁のすべてについて、同様の値が得られます。これらの値を使用して、セルの地下水量収支残余 Rvol が計算され、出力ラスターに書き込まれます。この値は、セルに流れ込むフロー ネットが与えられた場合の各セルの余剰水量 (負の値の場合は不足水量) を表し、次式で計算されます。
理想的には、この残余 Rvol はすべてのセルで 0 になります。残余を含む出力ラスターを調べるときには、0 からの差を探します。正または負の残余が大きい場合、大量の増加または減少があることを示し、これは連続性の原則に違反しており、水頭と透水率のデータが一貫していない可能性を示唆します。正または負の残余が一貫して発生するパターンは、未特定のソースまたはシンクがあることを示唆します。モデル化を進める前に、残余を減少します。通常、残余を減少するには、透水率のフィールドを調整します。
流向ベクトルの計算
各セルについて流向ベクトルを計算する [ダルシー フロー (Darcy Flow)] で使用される実際の式は、Ux(i-1/2,j) と Ux(i+1/2,j) の算術平均を、中央セルの間隙率 ni,j と層厚 bi,j で除算する処理をまとめたもので、次式に示すように中心における透水流束 Vx が得られます。
また、同様の式を使用して中心の Vy が計算されます。
この中心の処理は、格納する値がセル中央の値を表すという規則に従うために行われます。これらの値は、地理座標で方向と大きさに変換され、出力の方向ラスターと大きさのラスターに格納されます。
情報が不完全なラスターの境界セルの場合、速度の値は、単純に最も近い内部セルからコピーされます。
間隙率の値
以下の表に、さまざまな地質媒体の間隙率と透水係数の値を示します。
表 1:未固結媒体の透水係数
| 媒体 | K (m/s) |
|---|---|
粗い礫 | 10-1 - 10-2 |
砂礫 | 10-1 - 10-5 |
細砂、沈泥、黄土 | 10-5 - 10-9 |
粘土、頁岩、漂礫土 | 10-9 - 10-13 |
表 2:固結媒体の透水係数
| 媒体 | K (m/s) |
|---|---|
ドロマイト質石灰石 | 10-3 - 10-5 |
風化石灰岩 | 10-3 - 10-5 |
未風化石灰岩 | 10-6 - 10-9 |
石灰石 | 10-5 - 10-9 |
砂岩 | 10-4 - 10-10 |
花崗岩、片麻岩、成形玄武岩 | 10-9 - 10-13 |
表 3:地質媒体の間隙率
| 媒体 | 全間隙率 |
|---|---|
未変質の花崗岩と片磨岩 | 0.0002 - 0.018 |
珪岩 | 0.008 |
頁岩、粘板岩、雲母片岩 | 0.005 - 0.075 |
石灰石、第一期ドロマイト | 0.005 - 0.125 |
第二期ドロマイト | 0.10 - 0.30 |
石灰岩 | 0.08 - 0.37 |
砂岩 | 0.035 - 0.38 |
火砕岩 | 0.30 - 0.40 |
砂 | 0.15 - 0.48 |
粘土 | 0.44 - 0.53 |
膨潤粘土、沈泥 | 最大 0.90 |
耕地土壌 | 0.45 - 0.65 |
その他の間隙率と透水係数の表が Freeze と Cherry の文献 (1979) に記載されています。Gelhar ら (1992) の文献に、さまざまな層の間隙率と透水係数のまとめが記載されています。堆積物質の間隙率についての詳しい考察が Blatt ら (1980) の文献にあります。(1980). これらの関数を用いる移流分散のモデル化に関する詳細な考察が、Tauxe (1994) の文献に記載されています。
例
地下水の分散モデリングの典型的なシーケンスは、ダルシー フロー (Darcy Flow)、粒子追跡 (Particle Track)、多孔質媒体内の分散 (Porous Puff) をこの順番どおりに実行するものです。
- ダルシー フロー (Darcy Flow) のツール ダイアログ ボックスでの設定例を次に示します。
入力 地下水の位置水頭 (groundwater head elevation) ラスター: head
入力有効地層間隙率 (effective formation porosity) ラスター:poros
入力飽和帯水層厚 (saturated thickness) ラスター:thickn
入力 地層透水率 (formation transmissivity) ラスター: transm
出力 地下水量収支残余 (groundwater volume balance residual) ラスター: resid1
出力方向ラスター:dir1
出力 マグニチュード ラスター: mag1
- ダルシー フロー (Darcy Flow) のツール ダイアログ ボックスでの設定例を次に示します。
入力 地下水の位置水頭 (groundwater head elevation) ラスター: head
入力有効地層間隙率 (effective formation porosity) ラスター:poros
入力飽和帯水層厚 (saturated thickness) ラスター:thickn
入力 地層透水率 (formation transmissivity) ラスター: transm
出力方向ラスター:dir1
出力 マグニチュード ラスター: mag1
参考文献
Bear, J. Hydraulics of Groundwater.McGraw-Hill. 1979
Blatt, H., G. Middleton, and R. Murray. Origin of Sedimentary Rocks, 2nd Ed. Prentice-Hall. 1980
Freeze, R. A., and J. A. Cherry. Groundwater.Prentice-Hall. 1979
Gelhar, L. W., C. Welty, and K. R. Rehfeldt. "A Critical Review of Data on Field-Scale Dispersion in Aquifers".Water Resources Research, 28 no. 7: 1955-1974. 1992.
Konikow, L. F. and J. D. Bredehoeft. "Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water", USGS Techniques of Water Resources Investigations, Book 7, Chap.C2, U.S. Geological Survey, Washington, D.C. 1978.
Marsily, G. de. Quantitative Hydrogeology.Academic Press. 1986.
Tauxe, J. D. "Porous Medium Advection-Dispersion Modeling in a Geographic Information System".Doctoral Dissertation in Civil Engineering.The University of Texas at Austin, 1994.