空間的に制限された多変量クラスター分析の詳細

周囲を見渡してみると、物事を組織化、グループ化、区別、分類することによって、それをより深く理解しようとすることが常にごく自然に行われています。このような分類プロセスは、学習と理解の基礎となります。同様に、データをより深く学習し理解するために、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを使用できます。作成するクラスターの数を指定すると、各クラスター内のすべてのフィーチャはできる限り類似していて、クラスター間はできる限り異質になるような解法を探します。フィーチャの類似性は、[分析フィールド] パラメーターに指定する属性のセットに基づくもので、必要に応じて、クラスターのサイズに対する制限を取り込みます。このツールが使用するアルゴリズムは、接続性グラフ (最小スパニング ツリー) および SKATER と呼ばれる方法を採用して、データ内の自然なクラスターおよびクラスターのメンバーシップの確率を評価するための証拠の蓄積を検索します。

ヒント:

クラスタリング、グループ化、および分類手法は、機械学習で最も広く使用されている方法です。[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールは、教師なし機械学習方法を使用して、データ内の自然なクラスタリングを決定します。これらの分類方法は、データのクラスタリングを決定するように誘導またはトレーニングするために、事前に分類されたフィーチャのセットを必要としないため、教師なしであると見なされています。

このようなクラスター分析のアルゴリズムは何百もありますが、すべて NP 困難として分類されます。すなわち、クラスター内の類似性とクラスター間の異質性の両方を完全に最大にする解法を見つけるには、クラスタリングするフィーチャを可能な限り組み合わせてみるしかありません。これは、フィーチャが少数の場合は実行可能ですが、すぐに実行困難になります。

最適な解法を見つけることが困難であるだけでなく、すべての可能なデータ シナリオに最適のクラスタリング アルゴリズムを特定することは非現実的でもあります。クラスターにはさまざまな形状、サイズ、密度があり、属性データにはさまざまな範囲、対称性、連続性、計測単位が含まれます。そのため、過去 50 年にわたって数多くのクラスター分析アルゴリズムが開発されてきました。ここでは、データ内の基礎となる構造をより深く理解するための予備ツールとして、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを採用するのが最適です。

適用例

このツールの適用例には、以下のようなものがあります。

• 動物のなわ張りを理解するために動物観察に関するデータを収集した場合、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールが役に立ちます。たとえば、鮭がそれぞれのライフ ステージでいつ、どこに集まってくるのかを知ることは、繁殖を助けるための保護領域を作るのに役立ちます。
• 農学者が、分析範囲のさまざまなタイプの土壌を分類することもできます。一連のサンプルである土壌の特性に対して [空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを使用すると、空間的に連続するが異なっている土壌タイプのクラスターを特定できます。
• 購買パターン、人口学的特性、移動パターンによって顧客をクラスタリングすると、自社製品の有効なマーケティング戦略を立案できます。
• 都市計画立案者は、多くの場合、都市を別々の区域に分けることによって、効率的に公的施設を配置し、地域を活性化して、地域の関わりを促進させる必要があります。都心のブロックの物理的特性と人口学的特性に対して [空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを使用すると、計画立案者は、物理的特性と人口学的特性が類似する都市の空間的に連続する領域を特定できます。
• 集約データに対して分析が行われる場合、統計的推論の既知の問題として生態学的錯誤が発生することがあります。多くの場合、分析に使用される集約方式が分析対象に適していないために発生します。たとえば、国勢調査データは人口分布に基づいて集約されますが、これは山火事の分析には適していません。可能な限りの最小集約単位を同種の領域に分割し、現在の分析対象に正確に対応する一連の属性を求めることが、集約の偏りを減らし、生態学的錯誤を避ける有効な方法です。

入力

このツールは、ポイントまたはポリゴン [入力フィーチャ]、[出力フィーチャクラス] のパス、1 つ以上の [分析フィールド]、作成する [クラスターの数] を表す整数値、および [空間的制限] のタイプ (クラスタリング アルゴリズム内で適用される) を入力値として受け取ります。クラスターごとのフィーチャの最小数または最大数、あるいはクラスターごとの属性値の合計の最小値または最大値のいずれかに関する [クラスター サイズ制約]、および [クラスターの最適数の評価に使用する出力テーブル] の設定に使用できる複数のオプションのパラメーターも複数あります。

分析フィールド

スケール率、間隔、等級計測システムを表す数値フィールドを選択します。ダミー (バイナリ) 変数を使用して、名目データを表すことができます。ただし、一般に、これらの変数は他の数値変数タイプのようには機能しません。たとえば、Rural という変数を作成して、各フィーチャ (国勢調査区域など) に対して、農村部である場合は 1、都市部である場合は 0 をそれぞれ割り当てることができます。ただし、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールで使用するためにこの変数をさらに適切に表現すると、各フィーチャに関連付けられた農村部の面積または割合になります。

メモ:

ばらつきの多い変数 (データ値が平均値付近で分散する) は、ばらつきの少ない変数よりもクラスターに大きい影響を与える傾向があるため、[分析フィールド] の値がこのツールで標準化されます。属性値の標準化には、Z 変換が含まれます。この変換では、すべての値の平均値を各値から引いた後、その結果をすべての値の標準偏差で割ります。標準化によって、属性が非常に異なる種類の数 (比率 (0 〜 1.0)、人口 (100 万以上)、距離 (キロメートルなど)) で表されている場合でも、すべての属性が同じスケールで表されます。

フィーチャのクラスターを区別する変数を選択する必要があります。たとえば、生徒が受けた標準学力試験の結果をもとに、校区をクラスタリングする場合を考えます。全体の試験得点、数学や国語といった特定科目の結果、試験得点の最低点を満たす生徒の割合などを含む [分析フィールド] を選択できます。[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを実行すると、R² 値が変数ごとに計算されて、メッセージ ウィンドウにレポートされます。たとえば以下のサマリーでは、校区は、生徒の試験得点、その領域で高校を卒業していない大人の割合、生徒 1 人あたりの支出、生徒と教師の平均割合に基づいてクラスタリングされます。TestScores 変数に最大 R² 値があることに注目してください。これは、この変数により、校区が最も効果的にクラスターに分割されることを示しています。R² 値は、クラスタリング プロセスの後、元の TestScores データのばらつきがどのくらい保持されていたかを表すため、特定の変数の R² 値が大きいほど、その変数はフィーチャを適切に区別します。

詳細:

R² 値は次のように計算されます。

(TSS - ESS) / TSS

ここで、TSS は二乗総和で、ESS は説明された二乗和です。TTS は、変数のグローバル平均値からの偏差を二乗して足したものです。ESS も同じ計算方法で求められますが、グループごとの偏差である点が異なります。各値をその値が属しているグループの平均値から引いた後、求められた結果を二乗して足します。

クラスター サイズ制限

クラスターのサイズは、[クラスター サイズ制限] パラメーターを使用して管理できます。各クラスターが満たす必要がある最小閾値または最大閾値を設定できます。サイズ制限は、各クラスターが含む [フィーチャ数] または [属性値] の合計のいずれかにすることができます。たとえば、経済的変数のセットに基づいて米国の郡をクラスタリングする場合、各クラスターに 500 万人の最小人口および 2500 万人の最大人口が存在することを指定できます。あるいは、各クラスターが 30 以上の郡を含む必要があると指定することもできます。

[クラスターあたりの最大値] 制限が指定された場合、アルゴリズムは 1 つのクラスターから開始し、空間的に連続している値が類似したクラスターを分割します。すべてのクラスターのサイズが [クラスターあたりの最大値] の値を下回るまで新しいクラスターが作成され、各分割ではすべての変数が考慮されます。

SKATER は、対象のフィーチャの類似する値を持つデータを空間的に分割することによって、クラスターを形成します。すべてのクラスターが [クラスター サイズ制限] パラメーターに従わない可能性もあります。これは、定義されたクラスター サイズ制限が最適なクラスター定義に役立たない場合に発生します。

SKATER は、指定されたすべての [分析フィールド] の類似する値を持つデータを空間的に分割することによっても、クラスターを形成します。すべてのクラスターが [クラスター サイズ制限] に従わない可能性もあります。これは、最大値制限および最小値制限の両方が互いに近いに値に設定された場合、または空間的制限に基づいて最小スパニング ツリーが制限された方法に起因して発生する可能性があります。これが発生した場合、このツールは終了し、指定された要件を満たさなかったクラスターがメッセージ ウィンドウにレポートされます。

クラスターの数

問題や課題に最適なクラスター数がすぐにわかる場合があります。たとえば、5 人のセールス マネージャーにそれぞれ隣接する担当領域を割り当てる場合は、[クラスターの数] パラメーターに「5」と指定します。ただし、多くの場合、特定のクラスター数を選択するための基準はなく、フィーチャの類似性と異質性を最適に区別する数を選択することになります。このような状況に対応するには、[クラスターの数] パラメーターを空白のままにし、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを使用して、フィーチャを 2 ～最大 30 クラスターに分割したときの有効性を評価します。クラスタリングの有効性は、クラスター間の分散とクラスター内の分散の間の比率である Calinski-Harabasz 疑似 F 統計を使用して計測されます。言い換えると、この比率は、グループ内の類似性およびグループ間の異質性を次のように反映します。

たとえば、4 つの空間的に隣接するクラスターを作成するとします。この場合、ツールは、フィーチャの空間構造とそれらが関連する分析フィールドの値の両方を反映する最小スパニング ツリーを作成します。次にツールは、ツリーを切断する最適な場所を決めて、2 つの別個のクラスターを作成します。次に、最適な 3 つのクラスターの解を得るには、作成された 2 つのクラスターのうちどちらのクラスターを分割するべきかを決定します。2 つのクラスターのうちの 1 つが分割され、もう一方はそのまま維持されます。最後に、最適な 4 つのクラスターの解を得るには、作成された 3 つのクラスターのうちどのクラスターを分割するべきかを決定します。分割された各クラスターにおける最適な解は、クラスター内の類似性とクラスター間の相違の両方を最大化する方法です。あるクラスター内のすべてのフィーチャの分析フィールドの値が同一である場合、そのクラスターは分割されません (恣意的である場合を除く)。作成されたすべてのクラスターが、それらの中に同一のフィーチャを含んでいる場合、指定した [クラスターの数] の値に達していなくても、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールは、新しいクラスターの作成を停止します。すべての [分析フィールド] に同一の値が含まれている場合、クラスターを分割するための基準がありません。

空間的制限

[空間的制限] パラメーターは、生成されたクラスターが空間的に近接することを保証します。フィーチャがクラスターの別のメンバーとエッジを共有する場合 (隣接エッジのみ)、あるいはエッジまたは頂点のいずれかを共有する場合 (隣接エッジ コーナー)、ポリゴン フィーチャクラスの [隣接] オプションが有効になり、フィーチャが同じクラスターの一部にのみなれることを示します。ただし、隣接していないポリゴンまたは隣接をまったく持たないポリゴンのクラスターがデータセットに含まれる場合、ポリゴン隣接オプションは適切な選択ではありません。

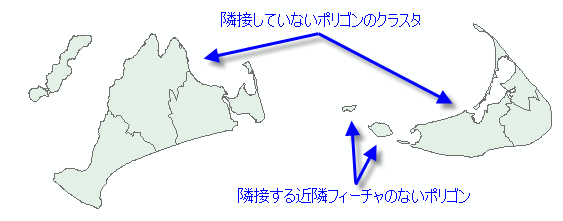
[切詰めドローネ三角形分割] オプションは、ポイント フィーチャまたはポリゴン フィーチャに適しており、少なくとも他の 1 つのクラスター メンバーが Natural Neighbor (ドローネ三角形分割) である場合に、フィーチャがクラスターに含められることを保証します。概念的に、ドローネ三角形分割はフィーチャの重心から三角形の重複しないメッシュを作成します。各フィーチャは 1 個の三角形ノードです。エッジを共有していノード同士は、互いに近傍と見なされます。その後、これらの三角形は、凸包にクリップされ、フィーチャが凸包の外のどのフィーチャとも隣接できないことを保証します。このオプションは、一致するフィーチャを持つデータセットには使用できません。また、ドローネ三角形分割法は、フィーチャをティーセン ポリゴンに変換して、データセット内の特にポリゴン フィーチャ、場合によっては周辺フィーチャとの近隣リレーションシップを決定するため、このオプションを使用しても必ずしも期待どおりの結果にはなりません。以下の図では、グループ化された元のポリゴンの一部が隣接していないことに注目してください。ただし、これらがティーセン ポリゴンに変換されると、グループ化されたフィーチャはすべて、隣接してエッジを共有します。

[切詰めドローネ三角形分割] では、ティーセン ポリゴンの隣接により、近隣リレーションシップが定義されます。

作成されたクラスターを空間的および時間的に隣接させたい場合、[空間ウェイト マトリックスの生成 (Generate Spatial Weights Matrix)] ツールを使用して、空間ウェイト マトリックス ファイル (SWM) を作成し、[空間リレーションシップのコンセプト] パラメーターで [時空間ウィンドウ] を選択します。これで、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを実行する際に、[空間ウェイト マトリックスの生成 (Generate Spatial Weights Matrix)] ツールを使用して作成した SWM ファイルを [ウェイト マトリックス ファイル] パラメーターに指定できます。

メモ:

フィーチャ間の空間リレーションシップは SWM ファイルに保存され、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールがこれを使用して空間的制限を適用しますが、グループ化プロセスに関与する実際の荷重はありません。SWM ファイルは、どのフィーチャが同じクラスターに含められるか、含められないかを追跡する場合にのみ使用されます。

最小スパニング ツリー

クラスターのメンバーシップを隣接フィーチャに制限するには、このツールでは、まずフィーチャ間の近隣リレーションシップを表す接続性グラフが作成されます。接続性グラフから、フィーチャの空間リレーションシップとフィーチャのデータの類似性の概要を示す最小スパニング ツリーが作成されます。フィーチャは、重み付けされたエッジに接続された最小スパニング ツリーのノードになります。各エッジの加重は、エッジが接続するオブジェクトの類似性に比例します。最小スパニング ツリーを作成したら、ツリーの枝 (エッジ) を切り取って、2 つの最小スパニング ツリーを作成します。切り取るエッジは、単体 (フィーチャが 1 つのみのクラスター) になるのを避け (可能であれば)、作成されたクラスターの相違を最小にするように選択します。それぞれの反復では、指定した [クラスターの数] を取得するまで、最小スパニング ツリーの 1 つがこの切り取り処理によって分割されます。使用される公開済みの方法は、SKATER (Spatial "K"luster Analysis by Tree Edge Removal) と呼ばれます。各反復では、クラスターの類似性を最適化する枝を選択して切り取りますが、これで最終結果が最適になる保証はありません。

メンバーシップの確率

[メンバーシップ確率を算出する場合の順列] パラメーターは、証拠の蓄積を使用してクラスターのメンバーシップの確率を計算するために実行する順列の数を定義します。メンバーシップの確率は、PROB フィールド内の出力フィーチャクラスに含まれます。高いメンバーシップの確率は、フィーチャが、それが割り当てられたクラスターに類似し、かつ近接しており、そのクラスターに属していることを確信できるということを示しています。低い確率は、フィーチャが、SKATER アルゴリズムによって割り当てられたクラスターとは非常に異なっているか、あるいは [分析フィールド]、[クラスターサイズ制約]、または [空間的制限] パラメーターが何らかの方法で変更された場合に、フィーチャを別のクラスターに含めることができるということを示している場合があります。

指定した順列の数は、SKATER の空間的制限を乱すために作成されるランダム スパニング ツリーの数を定義します。その後アルゴリズムは、ランダム スパニング ツリーごとに、指定された [クラスターの数] の解を求めます。順列処理は、SKATER によって定義された元のクラスターを使用して、クラスターのメンバーが変更中のスパニング ツリーの下で一緒にクラスタリングされる頻度を追跡します。スパニング ツリーに対するわずかな変化によってクラスターが切り替わりやすいフィーチャには小さいメンバーシップの確率が与えられ、クラスターが切り替わらないフィーチャには大きいメンバーシップの可能性が与えられます。

大きいデータセットに対して実行する場合、これらの確率の計算にはかなりの時間がかかる可能性があります。まず反復処理を行って分析に最適なクラスター数を特定し、次に以降の分析の実行で確率を算出することをお勧めします。[並列処理ファクター] の [環境] 設定を 50 に増やすと、パフォーマンスが向上することもあります。

出力

[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールでは、数多くの出力が作成されます。これらのメッセージには、[ジオプロセシング] ウィンドウからアクセスできます。そのためには、プログレス バーの上にカーソルを置くか、ツールの進行状況ボタン をクリックするか、[ジオプロセシング] ウィンドウの下部にあるメッセージ セクションを展開します。ジオプロセシング履歴を介して、以前に実行した [空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] のメッセージにアクセスすることもできます。

[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールのデフォルトの出力は、分析で使用されるフィールドと、各フィーチャが属するグループを特定する CLUSTER_ID という名前の新しい整数フィールドを含む、新しい出力フィーチャクラスです。この出力フィーチャクラスは、CLUSTER_ID フィールドに適用される固有のカラー レンダリング スキーマによって、コンテンツ ウィンドウに追加されます。

[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] の出力。

[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] のチャート出力。

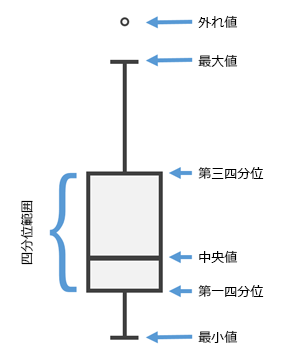
作成されたクラスターを集計するために、複数のタイプのチャートが作成されます。[箱ひげ図] は、各クラスターの特徴および解析で使用された各変数の特徴の両方に関する情報を示すために使用されます。下の図は、作成された [分析フィールド] およびクラスターごとの箱ひげ図およびそれらのサマリー値 (最小データ値、第 1 四分位値、グローバル中央値、第 3 四分位値、最大データ値、およびデータの外れ値 (四分位範囲よりも 1.5 倍小さい、または大きい値)) を解釈する方法を示しています。 これらの値および四分位範囲の値を確認するには、チャート上の箱ひげ図の上にポインターを置きます。最小値または最大値 (上または下のひげ) の外側にあるポイント マークは、データの外れ値を表します。

詳細:

四分位範囲 (IQR) は、第 3 四分位から第 1 四分位を引いたものです。 下の外れ値は 1.5 * IQR よりも小さい値 (Q1 - 1.5 * IQR) で、上の外れ値は 1.5 * IQR よりも大きい値 (Q3 + 1.5 * IQR) です。外れ値は、箱ひげ図ではポイント シンボルで表示されます。

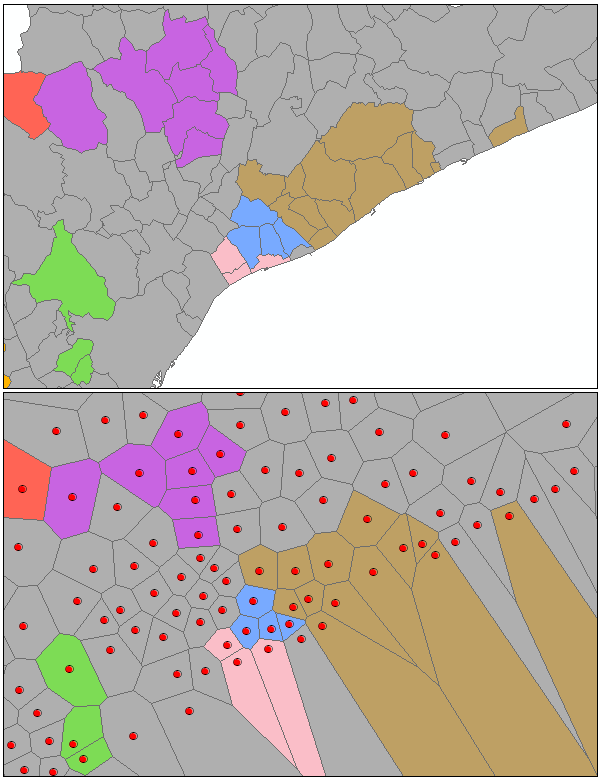
デフォルトの平行箱ひげ図では、クラスターと変数の両方の概要が表示されます。たとえば、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールが国勢調査地区に対して実行され、4 つのクラスターが作成されました。次のチャートでは、クラスター 2 (赤) は、賃貸料の平均値、母子家庭世帯数 (FHH_CHILD) の最大値、住戸数 (HSE_UNITS) の最大値、5 歳未満の子供の数の最大値を含む区域を表していることがわかります。クラスター 2 (鮮やかな黄色) は、賃貸料の最大中央値、母子家庭世帯数のほぼ最小値、および平均値を上回る住戸数を含む区域を表しています。クラスター 3 (緑) は、母子家庭世帯数の最小値、5 歳未満の子供の数の最小値、住戸数の最小値、および賃貸料のほぼ最低値 (ただし、クラスター 1 ほどは低くない) を含む区域を表しています。[分析フィールド] ごとのクラスターの平均値を確認するには、平均ラインの各ノードの上にポインターを置きます。

上の平行箱ひげ図を使用して解析のグローバル サマリーを調べた後に、[チャート プロパティ] ウィンドウの [シリーズ] タブで [並べて表示] に切り替えることによって、変数ごとに各クラスターの箱ひげ図を調べることができます。このデータ表示では、どのグループに各変数内の値の最大と最小の範囲があるかがわかります。箱ひげ図は、各変数についてクラスターごとに作成されるため、各クラスターの値が作成された他のクラスターにどのように関連しているかを確認することができます。各クラスター内の変数ごとの最小値、最大値、および中央値を確認するには、各変数の箱ひげ図の上にポインターを置きます。たとえば、下のチャートでは、クラスター 4 (金色) に MEDIANRENT 変数の最大値が存在し、354 ～ 813 の範囲の値を持つ区域が含まれていることがわかります。

クラスターあたりのフィーチャ数を示すバー チャートも作成されます。各バーを選択すると、マップ内のクラスターのフィーチャも選択されます。この機能は、さらに解析する場合に役立つことがあります。

[クラスターの数] パラメーターを空のままにした場合、このツールはデータに基づいてクラスターの最適数を評価します。[クラスター数の評価に使用する出力テーブル] のパスを指定すると、計算された疑似 F 統計値を示すチャートが作成されます。グラフ上の最高のピークが最大 F 統計量で、指定したフィーチャと変数を最も効果的に区別するクラスターの数を示します。以下のチャートでは、4 つのグループに関連付けられた F 統計量が最大です。疑似 F 統計量の高い 5 つのグループを選択してもかまいません。

クラスターの最適数を評価するための疑似 F 統計チャート

ベスト プラクティス

可能な限り多くの [分析フィールド] を含めたい傾向がありますが、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールは単一の変数およびビルドで開始することにより最適に機能します。分析フィールドの数が少ないほうが、結果の解析が容易になります。また、フィールドの数が少ないと、どの変数が最適な区別を実行するか判断しやすくなります。

多くのシナリオでは、[空間的に制限された多変量クラスター分析 (Spatially Constrained Multivariate Clustering)] ツールを何度も実行して、最適な [クラスターの数]、最も効果的な [空間的制限]、フィーチャをクラスターに最適に分類する [分析フィールド] の組み合わせを見つけることになります。

このツールがクラスターの最適数として 30 を返した場合、F 統計量のチャートを必ず調べてください。クラスターの数を選択して F 統計量のチャートを解釈することは、高度な技術を要し、クラスターの数が少ないほど、解析により適している場合があります。

参考資料

Duque, J. C.、R. Ramos、および J. Surinach 2007. 「Supervised Regionalization Methods: A Survey」International Regional Science Review 30: 195-220.

Assuncao, R. M.、M. C. Neves、G. Camara、および C. Da Costa Freitas 2006. 「Efficient Regionalisation Techniques for Socio-economic Geographical Units using Minimum Spanning Trees」International Journal of Geographical Information Science 20 (7) : 797-811.