説明
モルワイデ図法は正積擬円筒図法で、2:1 の比率の軸を持つ楕円として世界を表します。この図法は、バビネ図法、楕円図法、ホモログラフ図法、またはホマログラフ図法とも呼ばれます。この図法は主題世界地図や、正確な面積を必要とするその他の世界地図に適しています。
モルワイデ図法は、1805 年に Karl B. Mollweide によって考案されました。ArcGIS Pro 1.0 以降と ArcGIS Desktop 8.0 以降で使用できます。
Esri
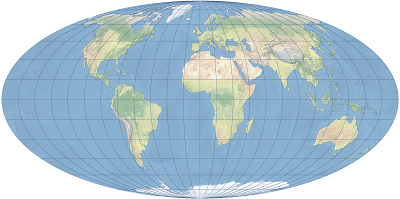
投影のプロパティ
次のサブセクションでは、モルワイデ図法のプロパティについて説明します。
経緯線
モルワイデは擬円筒図法です。赤道と中心子午線は 2 本の垂直線として投影されます。中心子午線は、投影された赤道の半分の長さになります。2 つの子午線 (中心子午線の 90°E と 90°W) は、円として投影されます。他の子午線は等間隔に並ぶ半楕円で、中心子午線に対してくぼんだ形状になります。すべての緯線は、中心子午線に対して垂直な不等間隔の直線です。その間隔は、赤道から離れるにつれて小さくなります。投影図のアウトラインは楕円形になります。極はポイントとして表され、楕円の頂点となります (短軸上)。経緯線は赤道と中心子午線に対して対称的です。
歪み
モルワイデ図法は、等積 (正積) 図法です。一般に、形状、方向、角度、距離には歪みが生じます。中心子午線の 40 度 44 分 N および S 上の点には歪みは生じません。縮尺は 40 度 44 分 N および S 上で正確にあり、特定の緯線に沿って一定になります。特に高緯度の場所では、外側子午線の隆起により、投影図のエッジに近づくにつれて著しい歪みが生じます。歪みの値は、赤道と中心子午線で対称的となります。
使用法
モルワイデ図法は小縮尺のマッピングに適しています。特に、地域の特徴を描写する世界全体の主題図や、正確な面積を必要とする分析に向いています。
バリアント
ArcGIS には 2 つのバリアントがあります。どちらのバリアントも、球体ベースの地球モデルを正確にサポートします。
- モルワイデ図法は ArcGIS Pro 1.0 以降と ArcGIS Desktop 8.0 以降で使用できます。楕円体の場合、このバリアントは長半径と球体の数式を使用します。
- モルワイデ図法球体補正は ArcGIS Pro 1.0 以降と ArcGIS Desktop 9.3 以降で使用できます。楕円体の場合、このバリアントでは球体補正タイプのパラメーターで指定された球体と、球体の数式を使用します。
制限事項
回転楕円体の場合、等面積のプロパティは、モルワイデ図法球体補正バリアントで球体補正タイプ 3 が使用されている場合にのみ保持されます。それ以外の場合は、面積は楕円体で保持されません。
パラメーター
モルワイデ図法のパラメーターは次のとおりです。
- 東距
- 北距
- 中央子午線
モルワイデ図法球体補正のパラメーターは次のとおりです。
- 東距
- 北距
- 中央子午線
- 球体補正タイプ、値は次のとおりです。
- 0 = 地理座標系の長半径か半径を使用
- 1 = 短半径または半径を使用
- 2 = 正積半径を計算して使用
- 3 = 正積半径を使用し、測地緯度を正積緯度に変換
ソース
Snyder, J. P. (1987). Map Projections: A Working Manual. U.S. Geological Survey Professional Paper 1395. Washington, DC: United States Government Printing Office.
Snyder, J. P. (1993). Flattening the Earth. Two Thousand Years of Map Projections. Chicago and London: University of Chicago Press.
Snyder, J. P. and Voxland, P. M. (1989). An Album of Map Projections. U.S. Geological Survey Professional Paper 1453. Washington, DC: United States Government Printing Office.