説明
二点正距図法は変更方位図法で、マップ上で選択した 2 つのポイントからの距離を維持します。2 つのポイントが同一であれば、投影図は正距方位図法になります。
この図法の数式は、1919 年に Hans Maurer が初めて考案しました。その 2 年後、Charles F. Close が 1921 年に独自にこの図法を提唱しました。ArcGIS Pro 1.0 以降と ArcGIS Desktop 8.0 以降で使用できます。
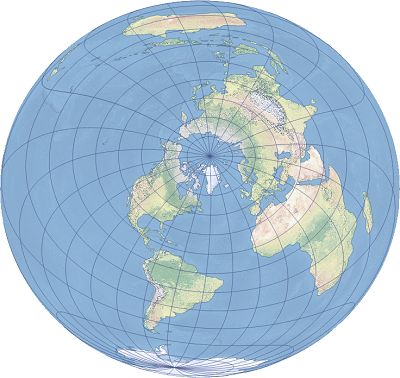
投影のプロパティ
次のサブセクションでは、二点正距図法のプロパティについて説明します。
経緯線
二点正距図法は、変更方位図法です。すべての子午線と緯線は複素曲線として投影されます。通常、極はマップ内のポイントとして示されます。経緯線は楕円体で囲まれます。2 つの中心点が長半径上にあり、その離心率は定義点の距離が離れるにつれて大きくなります。一般に、2 つの定義点を接続する線が子午線か赤道上にある場合を除き、経緯線は対称的にはなりません。
歪み
二点正距図法は正角でも正積でもありません。一般に、形状、面積、距離、方向、角度には全体的に歪みが生じます。選択した 2 つのポイントから地図上の任意のポイントまでのすべての距離は正確です。このポイントからの直線は大円の正確な長さを表現しますが、大円の正しい経路ではありません。
使用法
二点正距図法は、米国地理学協会によって、アジアの地図用に使用されていました。マップ上の既知の地点の関係を表す特殊な地図用途に適しています (たとえば、船や飛行機の航路の出発地点から到着地点までの距離など)。
制限事項
二点正距図法球体でのみサポートされます。楕円体の場合、半長軸が半径として使われます。楕円体を使用する場合、一部の正距プロパティは維持されません。
パラメーター
二点正距図法のパラメーターは次のとおりです。
- 東距
- 北距
- 最初のポイントの緯度
- 2 番目のポイントの緯度
- 最初のポイントの経度
- 2 番目のポイントの経度
特定のパラメーターを使用するケース
2 つのポイントが同一である場合は、正距方位図法による投影図となります。
ソース
Snyder, J. P. (1993). Flattening the Earth. Two Thousand Years of Map Projections. Chicago and London: University of Chicago Press.
Snyder, J. P. and Voxland, P. M. (1989). An Album of Map Projections. U.S. Geological Survey Professional Paper 1453. Washington, DC: United States Government Printing Office.
Thomas, P. D. (1970). Spheroidal Geodesics, Reference Systems, & Local Geometry. Washington, DC: United States Naval Oceanographic Office.