詳細
ワグナー図法 (第 4 図法) は、世界地図向けに設計された正積擬円筒図法です。子午線が半楕円になるエケルト図法 (第 4 図法) と比べ、ワグナー図法の子午線は楕円の一部に沿っています。
ワグナー図法 (第 4 図法) は、1932 年に Karl Heinrich (Karlheinz) Wagner によって考案されました。1934 年には、Reinholds V. Putniņš も独自にこの図法を考案したため、Putniņš P'2 図法とも呼ばれます。この図法は ArcGIS Pro 1.2 以降と ArcGIS Desktop 10.4 以降で使用できます。
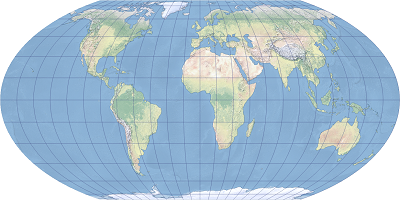
投影のプロパティ
次のサブセクションでは、ワグナー図法 (第 4 図法) のプロパティについて説明します。
経緯線
ワグナー図法 (第 4 図法) は擬円筒図法です。中心子午線以外の子午線は楕円の一部に沿っており、中心子午線から隆起した形になります。中心線から 103°55' 離れた位置の子午線は円弧です。中央子午線は、投影された赤道の半分の長さの直線になります。すべての緯線は、中心子午線に対して垂直な不等間隔の直線です。両極は、赤道の半分の長さの直線として表示されます。経緯線は赤道と中心子午線に対して対称的です。
歪み
ワグナー図法 (第 4 図法) は、等積 (正積) 図法です。形状、方向、角度、距離には歪みが生じ、熱帯地域や中緯度地方で南北方向に広がります。極に近づくにつれて、フィーチャは南北方向に圧縮されます。中心子午線の 42 度 59 分 N および S 上の点には歪みは生じません。歪みの値は、赤道と中心子午線で対称的となります。
使用法
この図法は小縮尺のマッピングに適しています。特に、地域の特徴を描写する世界全体の主題図や、正確な面積を必要とする分析に向いています。
制限事項
回転楕円体の場合、測地緯度はまず正積緯度に変換され、正積半径が半径として使用されます。
パラメーター
ワグナー図法 (第 4 図法) のパラメーターは次のとおりです。
- 東距
- 北距
- 中央子午線
- 原点の緯度
ソース
Wagner, K. (1932). "Die Unechten Zylinderprojektionen." Aus dem Archiv der Deutschen Seewarte, 51 (4).
Putniņš, R. (1934). "Jaunas projekci jas pasaules kartēm." Geografiski Raksti, Folia Geographica 3 and 4, p. 180-209.
Snyder, J. P. and Voxland, P. M. (1989). An Album of Map Projections. U.S. Geological Survey Professional Paper 1453. Washington, DC: United States Government Printing Office.