Spatial Analyst のライセンスで利用可能。
3D Analyst のライセンスで利用可能。
[サーフェス パラメーター (Surface Parameters)] ツールは、傾斜方向、傾斜角、曲率など、ラスター サーフェスのパラメーターを決定します。
傾斜方向
[傾斜方向] サーフェス パラメーターは、下りの傾斜角が指している方向を特定します。 出力ラスターの各セルの値は、その位置でサーフェスが向いている方位方向を示しています。 傾斜方向は、0 度 (真北) ~ 360 度 (真北) で右回りに計測され、完全に円になります。 下り方向のない平坦な領域には -1 という値が割り当てられます。

以下の図に、入力標高データセットと出力傾斜方向ラスターを示します。

傾斜方向の適用例
[傾斜方向] サーフェス パラメーター タイプでは、次の操作を行えます。
- スキーに最適な斜面を検索する際に、ある山の北側斜面をすべて検出する。
- 各地の生活の多様性を調べる研究の一環として、ある地域の各場所における直射日光照度を計算する。
- 雪解け水が最初に流れ込む可能性がある住宅地域を特定する研究の一環として、山岳地域の南に面する傾斜のうち、雪が最初に融ける場所を検出する。
測地線傾斜方向の計算
ある位置における測地線傾斜方向は、楕円体表面に接する平面上 (下図で青色の平面) での、北を基準とした下り斜面の角度の方向 α を表しています。

各位置の傾斜方向を計算するために、二次または四次のサーフェスが、最小二乗法 (LSM) を使用して、近傍のセルとフィッティングされます。 サーフェスの法線は、そのサーフェスからのセルの位置で計算されます。 また、同じ位置で、楕円表面の接平面に垂直である楕円体の法線も計算されます。
楕円体表面の接平面が参照平面と見なされるため、サーフェス法線は平面上に垂直に投影されます。 最後に、北方向から時計回りに計測したサーフェス法線の投影の角度 α から、測地線傾斜方向が計算されます (上図を参照)。
傾斜角
[傾斜角] サーフェス パラメーターは、ラスター サーフェスの各セルの傾斜を表します。 傾斜角の値が小さくなるほど地表は平らになり、傾斜角の値が大きくなるほど地表が急勾配になります。
出力傾斜角ラスターは、「度」と「パーセント (勾配率)」の 2 種類のうち、いずれかの単位で計算できます。 勾配率は、「高低差÷距離 x 100」で求めることができます。 たとえば、下図の三角形 B の場合、 角度 45 度なので「高低差」と「距離」が等しく、勾配率は 100% になります。 三角形 C のように、傾斜角が垂直 (90 度) に近づくと傾斜率は無限に近づき始めます。

傾斜は多くの場合、次の画像に示すように標高データセットに対して実行されます。 この出力傾斜角ラスターでは、傾斜の急な斜面が暗褐色で表示されています。

人口データなど、他の種類の連続データでこのツールを使用して、値 (人口) の急激な変化を調べることもできます。
測地線傾斜角の計算
測地線傾斜角は、地形サーフェスと楕円体表面との間に形成される角度を表しています。 楕円体表面に平行であるサーフェスの傾斜角は 0 になります。 各位置の傾斜角を計算するために、二次または四次のサーフェスが、最小二乗法 (LSM) を使用して、近傍のセルとフィッティングされます。 サーフェスの法線は、そのサーフェスからのセルの位置で計算されます。 また、同じ位置で、楕円表面の接平面に垂直である楕円体の法線も計算されます。 度単位の傾斜角は、楕円体の法線と地形サーフェスの法線との間の角度から計算されます。 この角度は、地形サーフェスと楕円体表面との間の角度と同じです。
サーフェス曲率の概要
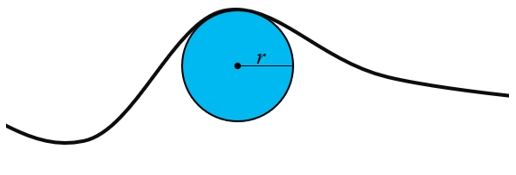
曲率は、サーフェスの形状を記述するため使用されるサーフェス パラメーター タイプのコレクションで、通常はサーフェスと平面との交差により作成されるサーフェス上のラインに沿ったものです。 概念的には、幾何学的曲率は任意のポイントにおける曲線の形状を近似するため最適な円 (接触円) を探すものです。 その円の半径の逆数 (1/r) が曲率になります。 したがって、直線に近いラインでは大きな円が最適となり、曲率は小さくなります。これに対して、鋭く曲がっているラインでは小さな円が最適で、曲率は大きくなります (Crane、2018)。
断面 (法傾斜) 曲率
[断面 (正規傾斜ライン) 曲率] サーフェス パラメーターは、斜面ラインに沿った幾何学的正規曲率を測定します。 これは「断面曲率」と呼ばれることもあり、サーフェスと交差する垂直面 (断面) の形状として視覚化できます。 下に示すように、この垂直面はオレンジ色のラインに沿ってサーフェスを切断し、切り取られた場合はサーフェスの断面図として表示されます。
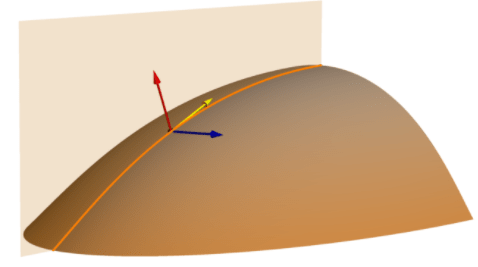
この平面は 2 つのベクターによって定義され、黄色の矢印は勾配の方向または傾斜ラインの矢印を、赤色の矢印はサーフェスの法線を表します。 これらの赤色と黄色のベクターの組み合わせにより、オレンジ色の平面と、サーフェスと交差するオレンジ色のラインが定義されます。 断面曲率は、オレンジ色の平面で、オレンジ色のライン (正規傾斜ライン) に沿って計算されます。
ここでは、以前の用語とのあいまいさや混乱を最小限に抑えるために、Mináretal (2020) の「正規傾斜ライン」という用語を採用します。
この曲率は通常、重力によってサーフェスに発生する下方への流れの加速と減速を特徴付けるために適用されます。 速度が速いほど、水は多くの物質を搬送して移動するため、加速の発生する領域は浸食が発生する領域に、減速の発生する領域は堆積が発生する領域になります。
下の図では、円錐の尾根の周囲での凸面の断面 (正規傾斜ライン) 曲率が高いエリアが、紫色で示されています。 円錐の底部での凹部の断面 (正規傾斜ライン) 曲率が高いエリアが、オレンジ色で示されています。 小さい曲率値を含むエリアは、透明です。

この曲率の結果は、以前の [曲率 (Curvature)] ツールからの断面曲率の出力とは異なります。 断面曲率と断面 (傾斜ライン) 曲率の相違点については、このページの後半で説明します。
断面 (正規傾斜ライン) 曲率は次の式で計算されます。
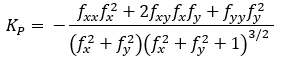
- 場所:
KP = 断面 (正規傾斜ライン) 曲率
z = f(x,y)
接線 (法輪郭) 曲率
[正接 (正規コンター) 曲率] サーフェス パラメーターは、コンター ラインに接する、勾配線に垂直な幾何学的法線曲率を測定します。 これは、コンター ラインに接する曲率を測定するため、正接曲率と呼ばれます。 青色のコンター ベクターと赤色のサーフェス法線ベクターにより定義される紫色の切断面により紫色の線が作成され、その線に沿って曲率が計算されるため、「正規コンター」として記述されます (Minár et al., 2020)。
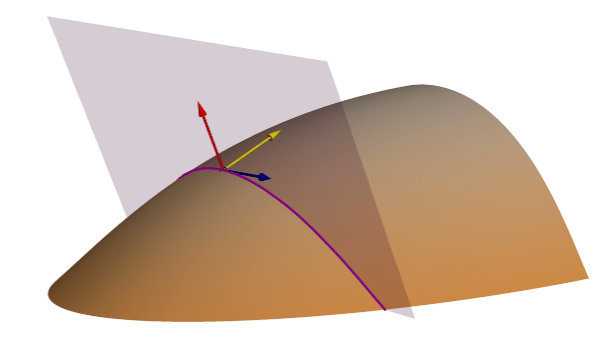
正接 (正規コンター) 曲率は通常、サーフェス上の流れの地形的な収束や分岐を特徴付けるために適用されます。
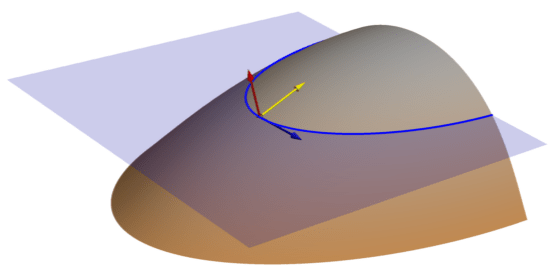
下の図では、円錐の尾根、およびこちらに向いている尾根の周囲での凸面の正接 (正規コンター) 曲率が高いエリアが、青色で示されています。 これらは、流れが分岐しているエリアです。 円錐の内部での凹面の正接 (正規コンター) 曲率が高いエリアが、収束している流れを赤色で示しています。 小さい曲率値を含むエリアは、透明です。

正接 (正規コンター) 曲率は次の式で計算されます。
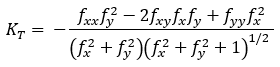
- 場所:
KT = 正接 (正規コンター) 曲率
z = f(x,y)
正接 (正規コンター) 曲率は投影コンター曲率と同じではありません。これらは、コンター曲率および水平曲率と呼ばれることもあります。 投影コンター曲率は、水平面がサーフェスと交差する青色のコンター ラインに沿って測定されます。 この種類の曲率は、現在のところ ArcGIS Pro では使用できません。
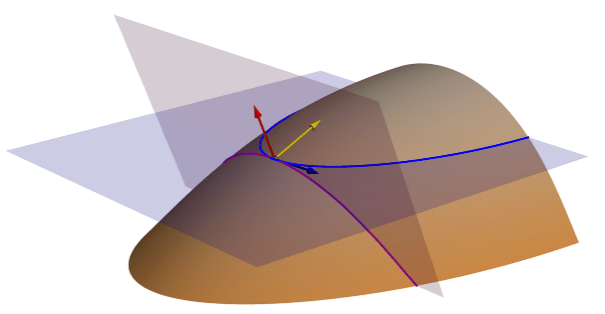
下図は、紫色のラインに沿って測定される正接 (正規コンター) 曲率と、青色のコンター ラインに沿って測定される投影コンター曲率との違いを示したものです。
平均曲率
[平均曲率] サーフェス パラメーターは、サーフェスの全体的な曲率を測定します。 最小曲率と最大曲率の平均として計算されます。 これは、断面 (正規傾斜ライン) と正接 (正規コンター) 曲率の平均値と数学的に同じです。 下図には、断面 (正規傾斜ライン) 切断面 (オレンジ色) と正接 (正規コンター) 切断面 (紫色) が示されています。
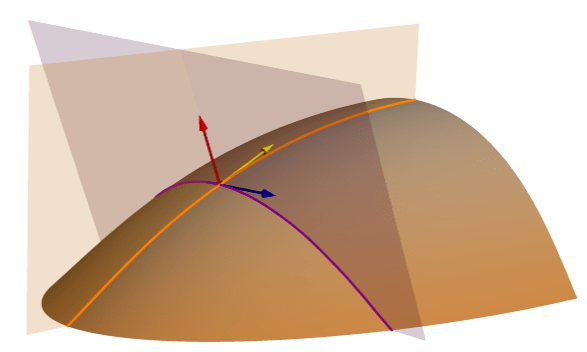
断面 (正規傾斜ライン) と正接 (正規コンター) の曲率はそれぞれ、特定の方向における凸面と凹面を測定します。 このとき平均曲率は、方向や重力の影響とは無関係に、サーフェス固有の凸面または凹面を表します。 この曲率の符号 (正または負) は、非常に大きな値でない限り凸面または凹面を決定的に示すものではありません。これは、サーフェスがある方向には凸面で、別の方向には凹面の場合があるためです。 高い正の値は最大の浸食エリアを示し、高い負の値は最大の堆積エリアを示します (Minár et al., 2020)。
平均曲率は次の式で計算されます。
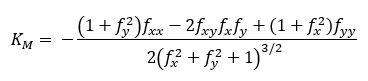
- 場所:
KM = 平均曲率
z = f(x,y)
従来の [曲率 (Curvature)] ツールのアルゴリズムとの比較
[サーフェス パラメーター (Surface Parameters)] ツールは、[曲率 (Curvature)] ツールと異なる曲率アルゴリズムを使用しており、計算における測地線の数式も異なるため、これら 2 つのツールの出力を直接比較してはいけません。 [サーフェス パラメーター (Surface Parameters)] の曲率タイプである断面 (正規傾斜ライン) および正接 (正規コンター) は、実際の幾何学的な曲率です (Minár および他の著者、2020)。 [サーフェス パラメーター (Surface Parameters)] の平均曲率は、そのポイントにおける最小と最大の曲率の平均値です。 [曲率 (Curvature)] ツールの断面および平面タイプは方向的な導関数で、ある位置におけるサーフェスの幾何学的な曲率を実際に測定したものではありません (Zevenbergen および Thorne、1987)。 [サーフェス パラメーター (Surface Parameters)] ツールの断面 (正規傾斜ライン) の符号 (正または負) は、[曲率 (Curvature)] ツールの断面曲率とは逆になります。 [サーフェス パラメーター (Surface Parameters)] ツールは測地線空間で計算を行い、[曲率 (Curvature)] ツールは平面座標と数式で計算を行います。 [サーフェス パラメーター (Surface Parameters)] ツールは二次または四次のサーフェスに適合できますが、[曲率 (Curvature)] ツールは四次のみをサポートします。
近傍距離
[近傍距離] は、現在処理中のセルから、直交する近傍の中心までの、マップ上の距離です。 近傍距離が小さいほど、地形内の局所的な変動の多くが補足され、小さな地形フィーチャの特徴が明確になります。 標高データの解像度が高い場合、近傍距離を大きくした方が適切な場合があります。これは、地形に対する目的の処理を反映していないデータの微細な誤差 (ノイズ) が発生する恐れがあるため、または距離が大きい方が目的の地形が認識しやすくなるためです。
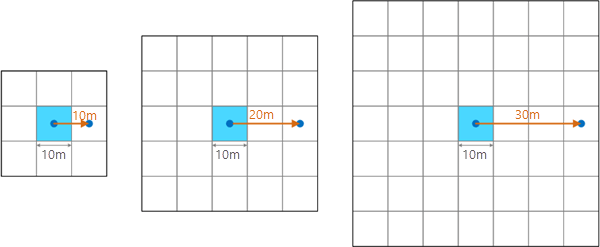
下の例では、断面 (正規傾斜ライン) 曲率の結果において示される著しいノイズおよび縞模様のアーティファクトを含む 5 メートルの分解能の数値表層モデル (DSM) が使用されています。 左の図では、デフォルトの 3 x 3 のウィンドウまたは 5 メートルの近傍距離、中央の図では、9 x 9 セルのウィンドウまたは 20 メートルの近傍距離、右の図では、15 x 15 セルのウィンドウまたは 35 メートルの近傍距離が使用されています。 この例では、近傍距離が増えるにつれて、地形の最も重要または主要なフィーチャがより明確になり、ノイズおよび縞模様のアーティファクトがあまり見えなくなります。 近傍距離が大きいほどノイズが必ず少なくなりますが、最適な距離は、データのセル サイズおよびアプリケーションにとって重要な地形フィーチャのサイズによって変わります。
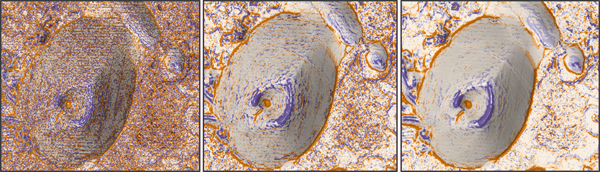
最小の近傍距離は、入力ラスターのセル サイズと同じです。 最大の近傍距離はセル サイズの 7 倍で、結果として 15 x 15 セルのウィンドウができます。 セル サイズの 7 倍よりも大きな近傍距離を指定した場合、常に 15 x 15 セルのウィンドウが使用されます。
指定された近傍距離がセル サイズの奇数倍にならない場合は、セル サイズの次の倍数に切り上げられます。 たとえば、上図で近傍距離 25 メートルが指定された場合、セル サイズの次の倍数である 30 メートル (セル サイズの 3 倍) に切り上げられ、7 x 7 セルのウィンドウになります。
目的の地形の分析に必要な空間分解能よりも標高データがはるかに細かい場合、近傍ウィンドウを使用する代わりに、データを用途に適した大きなセル サイズにリサンプリングまたは集約する方法があります。
サーフェス パラメーターの計算は、セル サイズと近傍距離に大きく影響されます。 Wilson (2018) と Minár および他の著者 (2020) は、この問題について数多くの研究の効果的で最新の要約を公表しています。
適応型近傍
[適応型近傍を使用] パラメーターをオンにすると、地形の関連する変化を適切に補足できるよう、サーフェス パラメーターの計算に使用される近傍距離 (ウィンドウ サイズまたはエリア) が変更されます。 このツールは、近傍に含まれるすべてのセルの値に基づき、平均標高 (DEV) (Wilson および Gallant、2000) からローカル偏差を計算し、適切なウィンドウ サイズを判定します。 可能な限り大きなウィンドウ サイズを使用し、サーフェスの偏差を最小化するよう試みます (James et al., 2014)。 使用される最大のウィンドウ サイズは、[近傍距離] パラメーターで指定されます。
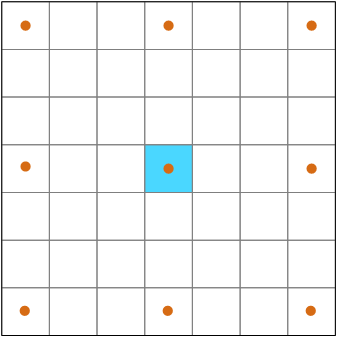
固定の近傍でサーフェス パラメーターを計算するとき、近傍に含まれるすべてのセルの値が使用されます。 適応型近傍でサーフェス パラメーターを計算するときは、近傍の 9 つのセル (直交または斜め方向のセルと中心の処理対象セル) のみが使用されます。
適応型近傍は、高分解能の DEM の中で、大きな丘陵地帯に小さな峡谷や小川が存在するなど、地形のフィーチャのサイズに大きな幅がある地形を分析するときに便利です。 このような状況では、小川や小峡谷には 1 メートルなどの小さな近傍距離が、丘陵には 10 メートルや 15 メートルなど大きな近傍距離が使用されます。
下図では、小川や崖縁などには小さな近傍、丘陵から平地への移行には大きな近傍、ほぼ平坦で一様な平原にはさらに大きな近傍が適切です。

近傍距離のエッジ効果
計算のため十分な情報が存在しない場合、出力の外縁のセルには NoData が割り当てられます。
適応型近傍オプションを使用しているとき、出力ラスターの範囲は外縁部で 1 セルだけ縮められます。
入力セルより大きい固定近傍距離を使用しているとき、出力ラスターの範囲は、使用している近傍距離に応じて縮小されます。 この縮小の量は (ピクセル単位のウィンドウ幅 - 1) / 2 で計算できます。
たとえば、近傍距離により 7 x 7 セルのウィンドウが使用される場合、出力ラスターは外縁の周囲で 3 セルだけ縮められます。
二次と四次
近傍ウィンドウにフィッティングできるローカル サーフェスには、二次と四次の 2 種類があります。 デフォルトは二次で、ほとんどのデータと用途に推奨されます。
二次サーフェスはポイントの最小二乗法によるフィッティングで、正確にすべてのポイントを通過するわけではありません。 すべてのポイントを正確に通過しないため、二次サーフェスを使用すると、高分解能のライダー サーフェスなど、ノイズの多いサーフェス データの影響を最小化でき、すべてのサーフェス パラメーターについてより代表的な結果が生成され、曲率の計算には特に重要です。
二次サーフェスは、セル サイズよりも大きい近傍サイズを指定する場合や、適応可能な近傍オプションを使用する場合に使用する必要があります。
四次サーフェスは、近傍セルのデータと正確にフィッティングします。 このオプションは、ランダム ノイズが存在しない、精度の高い入力サーフェスに適しています。 近傍距離が入力ラスター セル サイズより大きい場合、四次サーフェス タイプの精度の利点が失われるため、近傍距離はデフォルト (セル サイズと同じ) のままにします。
測地座標変換
[サーフェス パラメーター (Surface Parameters)] ツールは、地球の形を楕円体と見なし、地心三次元座標系 (Earth Centered、Earth Fixed (ECEF) 座標系とも呼ばれます) ですべての計算を行います。 データセットの投影方法は、この計算結果に影響しません。 入力ラスターの Z 単位が空間参照で定義されている場合は、この単位が使用されます。 入力の空間参照で Z 単位が定義されていない場合は、Z 単位パラメーターを使用して定義する必要があります。
ECEF 座標系は、地球の中心を原点とする三次元の右手直交座標系です。この座標系では、すべての位置が X、Y、Z 座標で表現されます。 次の図は、地心座標により表された目標位置 T の例です。

サーフェス ラスターは、入力座標系から地心三次元座標系に変換されます。
測地線計算では、測地座標 (緯度 φ、経度 λ、高度 h) に基づいて計算される X, Y, Z 座標を使用します。 入力サーフェス ラスターの座標系が投影座標系 (PCS) である場合は、最初に、各位置に測地座標が含まれているラスターが地理座標系 (GCS) に再投影され、その次に ECEF 座標系に変換されます。 高度 h (Z 値) は楕円形表面を基準とする楕円体の高さです。 次の図をご参照ください。

ECEF 座標を測地座標 (緯度 φ、経度 λ、高度 h) に変換するには、次の式を使用します。
X = (N(φ) + h) * cos(φ) * cos(λ)Y = (N(φ) + h) * cos(φ) * sin(λ)Z = (b2 / a2 * N(φ) + h) * sin(φ)- ここで、
N(φ) = a2 / √( a2 * cos(φ)2 + b2 * sin(φ)2)φ = 緯度
λ = 経度
h = 楕円体の高さ
a = 楕円体の長軸
b = 楕円体の短軸
上記の式で、楕円体の高さはメートル単位です。 ご使用の入力ラスターの Z 単位がこれ以外の単位で指定されている場合は、内部的にメートルに変換されます。
参考トピック
サーフェスの分析方法とその用途の詳細については、以下の参照資料をご参照ください。 また、Hengl and Reuter (2008) と Wilson (2018) はどちらも、これらのものを含む多くの地形分析技法とその用途について、包括的なリストを作成しています。 Minár および他の著者 (2020) は、地形サーフェス曲率に関する従来の作業について、多くの種類の曲率の明確化と定義を含めて、包括的な要約と比較を行っています。
参照先
B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice Section 10.2.1. p. 282.
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York)、190 pp
Crane K., 2018. Discrete Differential Geometry: An Applied Introduction Notices of the AMS、Communication: https://www.cs.cmu.edu/~kmcrane/Projects/DDG/paper.pdf
David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC)、pp. 3
E.J.Krakiwsky、D.E.Wells 共著、1971、 Coordinate Systems In Geodesy (GEODESY AND GEOMATICS ENGINEERING, UNB)、LECTURE NOTES、No16、1971、pp. 18-38
Hengl T. および Reuter H.、2008 Geomorphometry Concepts, Software, Applications Elsevier.
James D.E., M.D. Tomer, S.A. Porter. 2014. 高解像度デジタル標高モデルからの越層的地形セグメンテーション (Trans-scalar landform segmentation from high-resolution digital elevation models)。 ESRI Annual Users Conference (2014 年 7 月、サンディエゴ、カリフォルニア) で示されたポスター。
Lancaster, P. および Šalkauskas, K、Curve and Surface Fitting: An Introduction London: Academic Press、1986。
Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY)、Vol. 60、No 2、2011、pp. 145-159
Minár, J., Evans, I. S., & Jenčo, M. (2020). 地表 (地形学) 曲率の定義の総合的体系、地球科学のモデリングと予測への応用についての影響 (A comprehensive system of definitions of land surface (topographic) curvatures, with implications for their application in geoscience modelling and prediction)。 Earth-Science Reviews, 103414. https://doi.org/10.1016/j.earscirev.2020.103414
Wilson J.P and Gallant, J.C. (Eds.) 2000. Terrain Analysis: Principles and Applications John Wiley & Sons, Inc.
Wilson J.P 2018 Environmental Application of Digital Terrain Modeling John-Blackwell, Inc.
Zevenbergen, L. W., and C. R. Thorne. 1987. Quantitative Analysis of Land Surface Topography Earth Surface Processes and Landforms 12: 47-56