Geostatistical Analyst のライセンスで利用可能。
When you have multiple datasets and you want to use cokriging, you need to develop models for cross-covariance. Because you have multiple datasets, you keep track of the variables with subscripts, with Zk(sj) indicating a random variable for the kth data type at location si. The cross-covariance function between the kth data type and the mth data type is then defined to be
C km (si,sj) = cov(Zk(si), Zm(sj))Here is a subtle and often confusing fact: C km (si ,sj) can be asymmetric: C km (si ,sj) ≠ C mk (si ,sj) (notice the switch in the subscripts). To see why, look at the following example. Suppose you have data arranged in one dimension, along a line, such as the following:
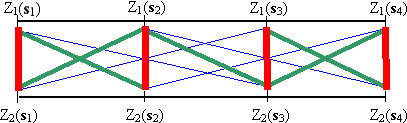
The variables for type 1 and 2 are regularly spaced along the line, with the thick red line indicating highest cross-covariance, the green line less cross-covariance, and the thin blue line the least cross-covariance, with no line indicating 0 cross-covariance. This figure shows that Z1(si) and Z2(sj) have the highest cross-covariance when si = sj, and the cross-covariance decreases as si and sj get farther apart. In this example, C km (si ,sj ) = C mk (si ,sj ). However, the cross-covariance can be "shifted":
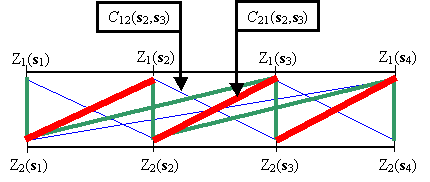
Notice that C12(s2,s3) now has the minimum cross-covariance (thin blue line) while C21(s2,s3) has the maximum cross-covariance (thick red line), so here Ckm (si ,sj) ≠ C mk (si ,sj). Relative to Z1, the cross-covariances of Z2 have been shifted -1 unit. In two dimensions, Geostatistical Analyst will estimate any shift in the cross-covariance between the two datasets if you click the shift parameters.
The empirical cross-covariances are computed as follows:
Average [ (z1(si) - 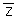 1) (z2(sj) -
1) (z2(sj) - 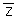 2)]
2)]
where Zk(si) is the measured value for the kth data set at
location si ,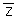 k is the mean for the kth dataset,
and the average is taken for all si and sj separated by a certain distance and angle. As for the semivariograms, Geostatistical Analyst shows both the empirical and fitted models for cross-covariance.
k is the mean for the kth dataset,
and the average is taken for all si and sj separated by a certain distance and angle. As for the semivariograms, Geostatistical Analyst shows both the empirical and fitted models for cross-covariance.
Choosing different cross-covariance models, using compound cross-covariance models, and choosing anisotropy will all cause the theoretical model to change. You can make a preliminary choice of model by seeing how well it fits the empirical values. Changing the lag size and the number of lags and adding shifts will change the empirical cross-covariance surface, which will cause a corresponding change in the theoretical model. Geostatistical Analyst computes default values, but you should feel free to try different values and use validation and cross-validation to choose the best model.