Spatial Analyst のライセンスで利用可能。
一連の概念ステップを利用すると、モデルを簡単に構築できます。 この一連のステップを理解するために、サンプルの課題を使って説明します。 都市計画担当者として、新しい学校に適切な建設地を見つける業務を委任されているとします。 ArcGIS Spatial Analyst エクステンションのツールを組み合わせて、候補地の特定に役立てることができます。
ステップ 1: 問題の定義
空間的問題を解決するには、解決しようとする問題点と達成目標をまず定義する必要があります。 作成すべきマップのタイプを具体化するために、目的とする出力の構想から始めます。
課題は、新しい学校を建設するための最適地を探すことです。 2 つのマップを生成する必要があります。 最初のマップは、各場所の相互に相対的な適合性を識別し、適合性マップと呼ばれます。 2 つ目のマップは、適合性マップから取得され、学校の機能的なニーズ (サイズおよび必要な形状) を考慮して、学校の実際の建設地を識別します。 これら 2 つのマップを作成するために、加重適合性モデルを生成します。
空間的問題のモデリングを簡単に実行できるようにするために、一連のステップをダイアグラムに記述します。 まずは、問題点の定義から始めます。 問題点の検討を進めるに従って、ダイアグラムを拡張し、目標に到達するために必要な一連の条件、プロセス モデル、および入力データセットを定義します。
ステップ 2: 問題点の分析
問題点の定義が終わったら、解決に必要な一連のステップが明確になるまで、問題点を細分化します。 細分化したステップが、解決すべき条件になります。
条件を定義する際は、それらの評価方法を検討します。 新しい学校に最適なエリアは、どのような方法で評価しますか。 学校の立地を検討するこの架空の例では、開発コストを最小限に抑えることが推進要因となります。 すでに何らかの形で開発されているエリアと比較すると、現在広々とした野原となっているエリアなど、特定の土地利用形態に建設する方が安く済みます。 もう 1 つの要因は地形です。通常は、急斜面よりも平坦なエリアに建設する方が容易です。 この町に引っ越してきた多くの家族は幼い子供を持つため、レクリエーション施設に近い場所を見つけるのが望ましいと言えます。 町全体にリソースを分散させるため、既存の学校から離れた場所を見つけることが重要です。 学校の機能的要件を満たすため、候補地には校舎と校庭を設けるための十分な大きさが必要となります。 土地の購入費用、学齢の子供の密度が最も高いエリアの特定など、より多くの条件を含めることができますが、このモデルは例示の目的で単純化されています。
これらの条件を満たすには、以下の情報を把握する必要があります。
- 土地利用形態は建設に適しているか
- 比較的平坦な土地はどこか
- レクリエーション施設に十分近いか
- 既存の学校から十分に離れているか
土地利用形態は建設に適しているか
建設候補地に適した土地利用形態であるかどうかを判断する必要があります。 これは、抱えている課題に従う主観的なプロセスです。 農地 (Agriculture) は、建設コストが最も安いと思われるので、最も望ましい土地です。 その次の候補は、荒地 (Barren)、雑木林 (Scrub Brush)、森 (Forest)、既存の市街地 (Built-up) の順になります。 この場合は関連するプロセス モデルがなく、土地利用 (Landuse) を入力データセットとして、建設に最適な土地利用形態の特定だけを行います。
- 必要な入力データセット: 土地利用 (Landuse)
比較的平坦な土地はどこか
比較的平坦な土地を持つエリアを見つけるには、土地の傾斜角を示すマップを作成する必要があります。 このプロセス モデルでは、土地の傾斜角を計算します。
- 必要な入力データセット: 標高 (Elevation)
レクリエーション施設に十分近いか
新しい学校はレクリエーション施設に近い方が望ましいので、レクリエーション施設までの距離を示すマップを作成し、レクリエーション施設に近いエリア内で新設校に適していると考えられる位置を探す必要があります。 このプロセス モデルでは、レクリエーション施設からの距離を計算します。
- 必要な入力データセット: レクリエーション施設の位置 (Rec_sites)
既存の学校から十分に離れているか
管轄区域の侵害を防止するため、新しい学校は既存の学校から離れた場所に建てる必要があります。 そのためには、既存の各学校までの距離を示すマップを作成する必要があります。 このプロセス モデルでは、既存の学校からの距離を計算します。
- 必要な入力データセット: 既存の学校の位置 (Schools)
ステップ 3: 入力データセットの調査
問題点を分析して一連の具体的な目標とプロセス モデルを定め、必要なデータセットが決まったら、入力データセットを調査し、その内容を把握する必要があります。 そのためには、問題点を解決し、データの傾向を知る上で重要な、データセット内の属性およびデータセット間の属性を把握します。
データを調査してみると、新設校の候補エリア、入力属性に対するウェイト、およびモデリング プロセスの変更に関して、重要な実態が得られることがよくあります。 既存の学校およびレクリエーション施設の位置が確認でき、標高が高い位置が elevation データセットからわかります。 また、landuse データセットを見ると、該当エリアの土地利用形態および他のデータセットとの関連性がわかります。
ステップ 4: 解析の実行
これまでに、一連の条件、要素とその相互作用、プロセス モデル、必要な入力データセットが明らかになっています。 これで、解析を実行する準備は整いました。
ArcGIS で解決されるタスクの多くについては、Esri Press  から入手可能な Esri Guide to GIS Analysis ブックをご参照ください。
から入手可能な Esri Guide to GIS Analysis ブックをご参照ください。
建設予定の新しい学校の理想的な場所を識別するこの例に向けた、一般的なプロセス ダイアグラムを次に示します。 付属のテキストで、各ステップの詳細な情報を提供します。
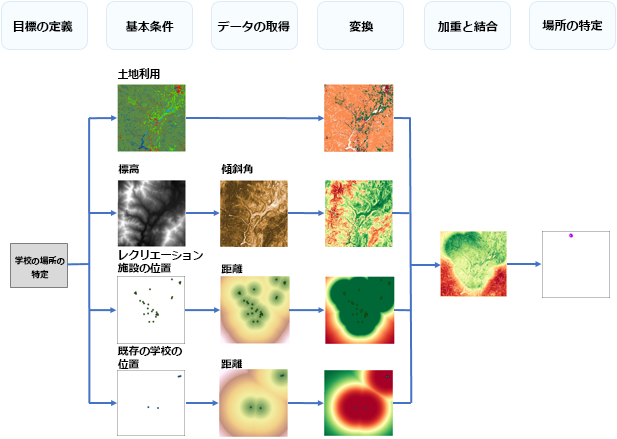
適合性マップの作成
適合性マップを作成すると、マップ上の各位置の適合値が得られます。
解析に必要なデータセット レイヤーが揃ったら (この例では、土地利用、傾斜角、レクリエーション施設までの距離、および他の学校までの距離)、それらのレイヤーをどのように組み合わせると、新設校の候補エリアを示すランク付きのマップを作成することができるでしょうか。 それには、一連のレイヤー間で値を比較する方法が必要になります。 さまざまなデータセット内の値を共通のスケールに変換することで、これを行うことができます。
各レイヤー内の各場所は、新設校の候補地としての適性に従ってランク付けされます。 たとえば、10 を最高値として、各レイヤー内の各場所に 1 ~ 10 のスケールに基づいて値を 1 つ割り当てることもできます。
これは、適合性スケールと呼ばれることがよくあります。 検討対象から外すエリアは、NoData を使うと除外することができます。 同一の数値スケールに基づいてすべてのレイヤーのランク付けを行うと、等しい重要性に基づいて最適な位置を決めることができます。 モデルは最初、このような方法で構築します。 その後、別のさまざまなシナリオのテストを進めるに従って、一連のレイヤーにさまざまなウェイト ファクターを適用すると、データおよびその関係をさらに調査することができます。
適合性スケールの作成
この例の場合と同様に、適合性スケールの多くの計測単位は人工的なものです。 適合性スケールにどのような計測単位が使用される場合でも、各計測単位は、最も適しているものから、最も適していないものまでの適合性のランクを付ける尺度、つまり優先度になります。 計測単位は、学校までの距離といった計測可能なものに基づく必要があります。 ただし、多くの場合は主観的な尺度になり、学校からの特定の距離が新設校の建設にどのくらい適しているのかを判断します。
人工的でない計測単位もあり、通常は、一部の条件と関連付けられます。 コストは、そのよい例ですが、十分詳細に定義する必要があります。 適合性の確立を調査する場合、不動産コストを抑えるという条件は、金銭的なスケール (ドル) に基づいて計測することになります。 そのようなスケールは、十分詳細に定義しなければなりません。 ドルのようにわかりやすいスケールの場合は、米ドルなのか豪州ドルなのか、貨幣間の換金率は、といったその他の可変要素もあります。
多くのスケールは、線形の関係にありません。しかし、それらのスケールは、時間やコストを節約したり、考慮しないオプションがあったりすることが原因で、線形関係で使われていることがよくあります。 たとえば、歩行距離にスケールを割り当てる場合、1km、5km、および 10km の歩行距離にそれぞれ 10、5、および 1 という適合性のランクは付けません。 5km の歩行は 1km の歩行のわずか 2 倍と受け止める人もいますし、10 倍と受け止める人もいるでしょう。
適合性スケールを作成する場合は、専門家とともに作業し、最高と最低のシナリオを定め、その中間ポイントをできるだけたくさん見つけるようにしてください。 そのような専門家は、検討対象の条件に精通している必要があります。 たとえば、交通量が最大と思われる時間を市の職員にたずねるよりも、運転に適した時間のランク付けを実際の通勤者にたずねた方が意味があります。
相反する目的と評価基準への対処について詳しくは、Jacek Malczewski 著『GIS and Multicriteria Decision Analysis』をご参照ください。
入力のランク付け
さまざまな入力を準備したら、それらを共通のスケールに変換する必要があります。
土地利用形態が適切なエリアへのランク付け
土地利用形態を示すマップにランクを付けるには、[再分類 (Reclassify)] ツールを使用します。 コストが関係するので、特定の土地利用形態に新設校を建設するのが望ましいため、該当する値にランクを付ける方法を決定する必要があります。
しかし、この例の場合は、どの土地利用形態が望ましいのかを判断する必要があります。 これは、調査に基づいて行う主観的な判断です。 建設に最適な土地利用形態および最も不適切な土地利用形態を判断する場合は、最適な候補を決めた後で最も不適切な候補を決めるのが簡単です。 それが終わったら、残っている土地利用形態から、最適な土地と最も不適切な土地を再度判断します。 そして、一連の土地利用形態が優先度の順に並ぶまで、この操作を繰り返して実行します。 Water (水域) という土地利用形態は建設が不可能であり、Wetlands (湿地) という土地利用形態は建設に対して制約があるため、この 2 つの形態は解析から除外してあります。 一連の土地利用形態に対するランク付けは、次の図のとおりです。
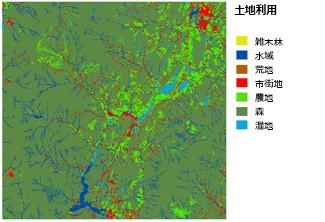
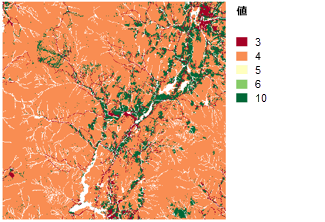
比較的平坦な土地にあるエリアへのランク付け
険しい地形を避け、比較的平坦な建設エリアを見つけるには、土地の傾斜角を知っておく必要があります。 [傾斜角 (Slope)] ツールでは、各セルから一連の近傍セルまでの高さの最大変化率をセルごとに識別し、そのマップを作成します。 生成されるラスターには、連続的に変化する浮動小数値として傾斜角が記録されます。 優先度は、傾斜角の値の変化に伴って直接変化すると考えられるため、[関数によるリスケール (Rescale by Function)] ツールを使用して、Linear 関数を適用することで、このマップにランクを付けます。 比較的平坦なエリアの方が望ましいため、傾斜角が急な場所には値 1、傾斜角が緩い場所には 10 を割り当てます。 それらの間の値は、次の図に示すように、線形的に調整されます。

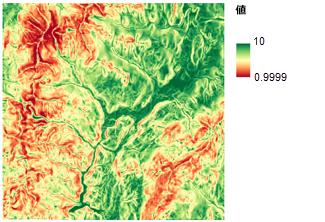
レクリエーション施設に近いエリアへのランク付け
レクリエーション施設に近い位置に学校を建設するには、レクリエーション施設までの距離を知っておく必要があります。 [ユークリッド距離 (Euclidean Distance)] ツールでは、任意の位置から最寄りのレクリエーション施設までの直線 (ユークリッド) 距離を計算し、そのマップを作成します。 得られるラスター データセットでは、どのセルも、最寄りのレクリエーション施設までの距離を表しています。 入力値は連続距離を表すため、このマップにランクを付けるには、[関数によるリスケール (Rescale by Function)] ツールを使用します。 レクリエーション施設に近い方がかなり望ましいため、MSSmall 関数を適用します。 これにより、レクリエーション施設に近い場所にかなり高い優先度の値が割り当てられ、遠い場所は優先度がかなり低くなります。 次の図に示すように、レクリエーション施設からの距離が 1 メートル変わるにつれて、優先度が連続的に変化します。
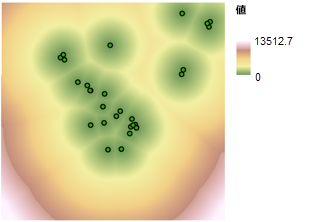
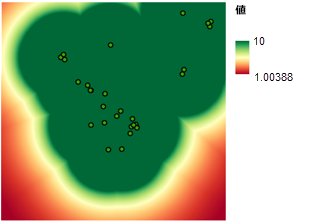
既存の学校から離れているエリアへのランク付け
他の学校の管轄区域に対する侵害を防止するため、既存の学校までの距離を知っておく必要があります。 [ユークリッド距離 (Euclidean Distance)] ツールでは、任意の位置から最寄りの学校までの直線距離を計算し、そのマップを作成します。 得られるラスター データセットでは、どのセルも、最寄りの学校までの距離を表しています。 このマップにランクを付けるには、もう一度 [関数によるリスケール (Rescale by Function)] ツールを使用します。 既存の学校から離れている方が望ましいため、Large 関数を使用して、既存の学校に最も近い距離には値 1、既存の学校から最も離れている距離には値 10 を割り当てます。 次の図に示すように、Large 関数では、場所が学校から 1 メートル離れるにつれて優先度が連続的に上がります。

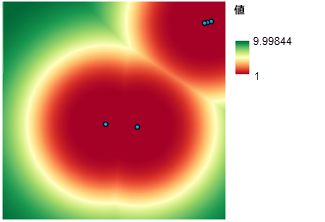
一連の適合性マップの結合
適合性モデルの最後のステップでは、土地利用形態、傾斜角、レクリエーション施設までの距離、学校までの距離の変換済み出力 (適合性マップ) を結合します。
適合性モデルの中で一部の条件を他より優先するには、データセットにウェイトを適用し、適合性モデルの中で重要性の高いデータセットに他より大きな影響率 (ウェイト) を割り当てます。 すべてのデータセットの重要度が等しい場合は、各データセットに同じウェイトを割り当てることができます。
この例では、問題点の分析から、新設校の建設場所として満たすべき最も望ましい条件はレクリエーション施設の近くであること、次に望ましい条件は既存の学校から離れていることです。 今回の適合性マップには、下記の影響率を割り当てます。 括弧内の値は、値を正規化するためにパーセンテージ値を 100 で割った値です。 各適合性マップには、正規化された値が乗数として使用されます。
適合性の割合
| 適合性係数 | 影響の割合 | 正規化された割合 |
|---|---|---|
レクリエーション施設までのランク付けされた距離 | 50% | (0.5) |
学校までのランク付けされた距離 | 25% | (0.25) |
ランク付けされた傾斜角 | 12.5% | (0.125) |
ランク付けされた土地利用形態 | 12.5% | (0.125) |
レクリエーション施設までの距離という適合性マップは最終的な結果に対して 50% (0.5) の影響度、学校までの距離という適合性マップは 25% (0.25) の影響度を持ちます。 傾斜角と土地利用形態はどちらも、12.5% (0.125) の影響度を持ちます。 適合性のスケールの割り当ての場合と同様に、ウェイトの割り当ても主観的なプロセスであり、検討時に最も重要になる条件によって左右されます。
最終的な適合性マップは、すべてのマップを結合して作成します。 ウェイトは、一連の適合性マップの結合時に割り当てることができます。 学校の建設地の最終的な適合性マップを以下の図に示します。 最適な位置を、濃緑で示します。 赤色の陰影部は、最も不適な位置です。
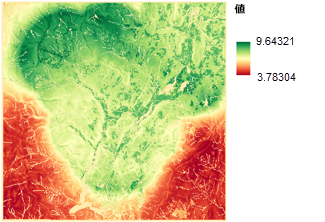
データセットを加重して結合するには、[マップ代数演算] を使用します。 別の方法として、[加重オーバーレイ (Weighted Overlay)] または [加重合計 (Weighted Sum)] ツールを使用することもできます。 モデル内でツールを使用した場合、元の画面に戻ってウェイト (影響の割合) および設定可能な任意のスケール値を簡単に変更することが可能です。 モデル内部でジオプロセシング ツールを接続し、モデルを 1 回作成すれば、パラメーター値を変更して異なる結果を調べることができます。
学校の場所の特定
このモデリング プロセスに対する最後のステップでは、実際に学校の場所を特定します。 最終的な適合性サーフェスは、土地利用形態、傾斜角、レクリエーション施設からの距離、および学校からの距離を基準として各場所の属性をランク付けしています。 ただし、建設予定の学校には、効率的に機能するための空間要件もあります。
学校に最適な場所は、運動場を設けることができる 150 エーカーの連続した土地の上に特定されます。 校舎の建設と保守の効率を高めるため、建設地の構成は比較的コンパクトである必要があります。
最終的な適当性サーフェスに対して [領域の特定 (Locate Regions)] ツールを使用し、最適な 150 エーカーの建設地を見つけます。
提案された用地を、前のステップの適合性マップと比較してください。
ステップ 5: 結果の確認
空間解析の結果が得られたら、その解析結果が正しいことを確認する必要があります。 その際、可能であれば、該当する用地を実際に訪れてみます。 重要な項目が、解析結果に反映されていないことがよくあります。 たとえば、該当地の風上に養鶏場があって強烈な臭いがするとか、市役所で過去の記録を調べた結果、該当する土地への建設に制約があったことが判明する場合もあります。 そのような場合は、該当する情報を解析に反映する必要があります。
ステップ 6: 結果の施行
空間モデルの最終ステップは、解析結果を施行し、選択した位置に新しい学校の計画および建設を開始することです。
適合性モデリングの詳細については、応用的解析のトピック「適合性モデリング ワークフローの概要」 をご参照ください。
をご参照ください。
参考情報
J. Malczewski 著 GIS and Multicriteria Decision Analysis Wiley & Sons, 1999.