傾斜角ツールの詳細—ArcGIS Pro

Spatial Analyst のライセンスで利用可能。

3D Analyst のライセンスで利用可能。

[傾斜角 (Slope)] ツールはラスターサーフェスの各セルの傾斜を特定します。傾斜角の値が小さくなるほど地表は平らになり、傾斜角の値が大きくなるほど地表が急勾配になります。

注意:

[サーフェスパラメーター (Surface Parameters)] ツールは、傾斜角を新たに実装するので、[傾斜角 (Slope)] ツールの代わりに使用することをお勧めします。 [傾斜角 (Slope)] ツールは平面を 9 個のローカルセルに収めますが、平面は地形の記述子としてあまり役に立たず、対象の自然変動がマスクされたり、強調されたりすることがあります。 [サーフェスパラメーター (Surface Parameters)] ツールは、サーフェスを平面ではなくセルの近傍に収めるため、地形をより自然に適合させることができます。

[傾斜角 (Slope)] ツールは、常に 3 x 3 のセルウィンドウを使用して値を計算し、[サーフェスパラメーター (Surface Parameters)] ツールは 3 x 3 から 15 x 15 のセルまでのウィンドウサイズを使用できます。高解像度の標高データには、大きいウィンドウサイズが便利です。これにより、地表面の処理を適切な縮尺で捉えられるようになります。 [サーフェスパラメーター (Surface Parameters)] にはアダプティブウィンドウオプションもあります。このオプションは地形のローカル変動を評価し、セルごとに最大の適切な近傍サイズを特定します。これは、河川、道路、傾斜の急変によって途切れる、緩やかな同種の地形において便利です。

以前のツールの実行と正確に一致する結果が必要である場合、またはアルゴリズムの正確さよりも高速な実行の方が重要である場合には、[傾斜角 (Slope)] ツールの従来のアプローチを引き続き使用できます。

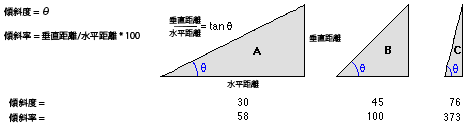
出力傾斜角ラスターは、「度」と「パーセント (勾配率) 」の 2 種類の単位で計算できます。勾配率は、「高低差÷距離 × 100」で求めることができます。たとえば、下図の三角形 B の場合、角度 45 度なので「高低差」と「距離」が等しく、勾配率は 100% になります。三角形 C のように、傾斜角が垂直 (90 度) に近づくと勾配率は無限に近づき始めます。

多くの場合、[傾斜角 (Slope)] ツールは、次の図に示すように標高データセットに対して実行されます。この出力傾斜角ラスターでは、傾斜の急な斜面が暗褐色で表示されています。

人口データなど、他の種類の連続データでこのツールを使用して、値 (人口) の急激な変化を調べることもできます。

計算方法とエッジ効果

傾斜角を計算する方法は 2 つあります。 [方法] パラメーターを使用して [平面] 計算を実行するか、[測地線] 計算を実行するかを選択できます。

平面方法の場合、傾斜角は、特定のセルの値と、その隣接セルの値とを比較したときの最大変化率として計測されます。二次元の直交座標系を使用し、投影された平面上で計算が実行されます。傾斜角の値は、3 次有限差分推定ツールを使用して計算されます。

測地線方法では、地球の形を楕円体と見なすことで三次元の直交座標系で計算が実行されます。傾斜角の値は、地形サーフェスと参照先の測地基準系との間の角度を計測することで計算されます。

平面計算と測地線計算のいずれもが、3 セル X 3 セルの近傍 (移動する枠) の使用によって実行されます。各近傍で、処理 (中央の) セルが NoData の場合、出力は NoData になります。また、計算を実行するには、処理セルに隣接しているセルのうち、少なくとも 7 つのセルが有効な値を保持している必要があります。有効なセルの数が 7 未満である場合、計算は実行されず、その処理セルの出力は NoData になります。

出力ラスターの最も外側のロウとカラムにあるセルは NoData になります。これは、これらのセルが、入力データセットの境界沿いにあり、必要なだけの有効な隣接セルに囲まれていないためです。

平面方法

中央セルから各隣接セルへの水平方向 (dz/dx) および垂直方向 (dz/dy) でのサーフェスの変化率 (差分) として傾斜角を計算します。傾斜角 (slope_radians) を計算するための基本的なアルゴリズムは次のとおりです。

slope_radians = ATAN ( √ ([dz/dx]² + [dz/dy]²) )

通常、傾斜角は「度」で計測され、次のアルゴリズムでもこの単位を使用しています。

slope_degrees = ATAN ( √ ([dz/dx]² + [dz/dy]²) ) * 57.29578

注意:

ここに示されている値 57.29578 は、180/pi の算出値を切り捨てたものです。

傾斜角アルゴリズムは次のように表すこともできます。

slope_degrees = ATAN (rise_run) * 57.29578

ここで、
```
rise_run = √ ([dz/dx]² + [dz/dy]²]
```

中央セルの値、およびそれを囲む 8 つのセルの値は、横方向の差分と縦方向の差分を決定します。隣接セルは a ～ i の文字で識別され、傾斜角の計算対象となるセルには e が割り当てられます。

セル e の X 方向の変化率は、次のアルゴリズムで計算されます。

[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize)

ここで、
wght1 と wght2 は有効なセルの水平加重計数値です。

次に例を示します。
- c、f、i の値がすべて有効である場合、wght1 = (1+2*1+1) = 4
- i が NoData の場合、wght1 = (1+2*1+0) = 3
- f が NoData の場合、wght1 = (1+2*0+1) = 2
隣接位置が a、d、g である場合を除き、同じようなロジックが wght2 にも適用されます。

セル e の Y 方向の変化率は、次のアルゴリズムで計算されます。

[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / (8 * y_cellsize)

ここで、
wght3 と wght4 は [dz/dx] の計算で見られたものと同じ概念を表しています。

平面上での傾斜角の計算例

例として、次のような移動ウィンドウの中心セルの傾斜角値を計算します。

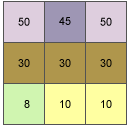
中央セル e の X 方向の変化率は、次のように計算されます。

[dz/dx] = ((c + 2f + i)*4/wght1 - (a + 2d + g)*4/wght2) / (8 * x_cellsize) = ((50 + 60 + 10)*4/(1+2+1) - (50 + 60 + 8)*4/(1+2+1)) / (8 * 5) = (120 - 118) / 40 = 0.05

中央セル e の Y 方向の変化率は、次のように計算されます。

[dz/dy] = ((g + 2h + i)*4/wght3 - (a + 2b + c)*4/wght4) / (8 * y_cellsize) = ((8 + 20 + 10)*4/(1+2+1) - (50 + 90 + 50)*4/(1+2+1)) / (8 * 5) = (38 - 190 ) / 40 = -3.8

X 方向と Y 方向の変化率を基に、中央セル e の傾斜角を次のように計算します。

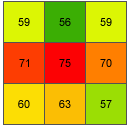
rise_run = √ ([dz/dx]² + [dz/dy]²) = √ ((0.05)² + (-3.8)²) = √ (0.0025 + 14.44) = 3.80032

slope_degrees = ATAN (rise_run) * 57.29578 = ATAN (3.80032) * 57.29578 = 1.31349 * 57.29578 = 75.25762

セル e の傾斜角値 (整数) は 75 度になります。

測地線方法

測地線方法では、地球の形を楕円体と見なすことで、地心三次元座標系 (Earth Centered、Earth Fixed (ECEF) 座標系とも呼ばれる) での傾斜角を計測します。データセットの投影方法は、この計算結果に影響しません。入力ラスターの Z 単位が空間参照で定義されている場合は、この単位が使用されます。入力の空間参照で Z 単位が定義されていない場合は、Z 単位パラメーターを使用して定義する必要があります。測地線方法では、平面方法と比べて、より精度の高い傾斜角が得られます。

測地座標変換

ECEF 座標系は、地球の中心を原点とする三次元の右手直交座標系です。この座標系では、すべての位置が X、Y、Z 座標で表現されます。次の図は、地心座標により表された目標位置 T の例です。

測地線計算では、測地座標 (緯度 φ、経度 λ、高度 h) に基づいて計算される X, Y, Z 座標を使用します。入力サーフェスラスターの座標系が投影座標系 (PCS) である場合は、最初に、各位置に測地座標が含まれているラスターが地理座標系 (GCS) に再投影され、その次に ECEF 座標系に変換されます。高度 h (Z 値) は楕円形表面を基準とする楕円体の高さです。次の図をご参照ください。

ECEF 座標を測地座標 (緯度 φ、経度 λ、高度 h) に変換するには、次の式を使用します。

X = (N(φ)+h)cosφcosλ

Y = (N(φ)+h)cosφsinλ

Z = (b²/a²*N(φ)+h)sinφ

ここで、
- N( φ ) = a²/ √(a²cosφ²+b²sinφ²)
- φ = 緯度
- λ = 経度
- h = 楕円体の高さ
- a = 楕円体の長軸
- b = 楕円体の短軸

上記の式で、楕円体の高さはメートル単位です。ご使用の入力ラスターの Z 単位がこれ以外の単位で指定されている場合は、内部的にメートルに変換されます。

傾斜角の計算

測地線傾斜角は、地形サーフェスと楕円体表面との間に形成される角度を表しています。楕円体表面に平行であるサーフェスの傾斜角は 0 になります。各位置の傾斜角を計算するために、3 セル X 3 セルの近傍平面が、最小二乗法 (LSM) を使用して、各処理セルの周りでフィッティングされます。 LSM による最適なフィットの位置では、実際の Z 値とフィッティング後の Z 値の差の二乗和 (SSD: Sum of Squared Differece) (dz_i) が最小化されます。例については、下の図をご参照ください。

平面は z = Ax + By + C で表されます。各セルの中心で、dz_i は実際の Z 値とフィッティング後の Z 値の差を示します。

∑⁹_i=1dz_i² が最小になったときに平面が最適にフィッティングされます。

平面のフィッティング後、そのセルの位置でサーフェスの法線が計算されます。また、同じ位置で、楕円表面の接平面に垂直である楕円体の法線も計算されます。

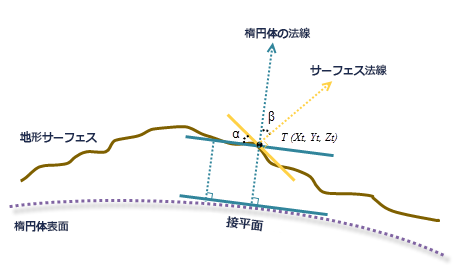
度単位の傾斜角は、楕円体の法線と地形サーフェスの法線との間の角度 (ここでは β で表す) から計算されます。上図の角度 α は測地線傾斜角であり、ジオメトリ一致の法則に従って角度 β と同じになります。

勾配 (%) として傾斜角を計算するには、次の式を使用します。

Slope_PercentRise = ATAN(β) * 100%

サーフェスパラメーター (Surface Parameter) ツールを使用すべきか

[入力ラスター] パラメーターの値 (Python の in_raster) が高解像度でセルサイズが数メートル未満の場合や、特にノイズが多い場合は、このツールの直接 3 × 3 近傍ではなく、[サーフェスパラメーター (Surface Parameters)] ツールとそのユーザー定義の近傍距離オプションを使用することを検討してください。より大きな近傍を使用することで、ノイズの多いサーフェスの影響を最小限に抑えることができます。また、高解像度のサーフェスを使用する場合は、より大きな近隣を使用することで、地形やサーフェスの特性をより上手く表現することができます。

GPU の使用

測地線方法の場合、このツールは、特定の GPU ハードウェアをシステムにインストールしている場合に、パフォーマンスの向上が可能です。このツールをサポートする方法、構成する方法、および有効化する方法の詳細については「Spatial Analyst での GPU 処理」をご参照ください。

参考文献

Marcin Ligas, and Piotr Banasik, 2011. Conversion between Cartesian and geodetic coordinates on a rotational ellipsoid by solving a system of nonlinear equations (GEODESY AND CARTOGRAPHY)、Vol. 60、No 2、2011、pp. 145-159

B. Hofmann-Wellenhof, H. Lichtenegger and J. Collins, 2001. GPS - theory and practice. Section 10.2.1. p. 282.

David Eberly 1999. Least Squares Fitting of Data (Geometric Tools, LLC), pp. 3.

注意: