Spatial Analyst のライセンスで利用可能。
3D Analyst のライセンスで利用可能。
[スプライン (Spline)] ツールでは値を推測する内挿法が用いられ、サーフェス全体の曲率を最小限に抑える数学関数を使用することで、入力ポイントを正確に通過する滑らかなサーフェスが得られます。
概念的背景
概念的には、サンプル ポイントがその値の高さまで伸ばされます。 スプラインは、ゴム シートのサーフェス全体の曲率を最小にするように、ゴム シートを曲げて入力ポイントを通過するように設定します。 これは、サンプル ポイントを通過するように、近傍にある指定数の入力ポイントに数学関数を当てはめます。 この方法は、標高、地下水面の高さ、汚染濃度など変化が小さいサーフェスの生成に最適です。
基本的な最小曲率スプライン内挿では、次の 2 つの条件に基づいてポイントが内挿されます。
- サーフェスはデータ ポイントを正確に通過すること。
- サーフェスの曲率が最小になること。 サーフェス上の各ポイントに渡される二次導関数項の二乗の累積合計が最小になるように内挿されます。
基本的な最小曲率手法は「薄板補間」とも呼ばれます。 連続する一次導関数サーフェスと併用することで、滑らかな (連続していて微分可能な) サーフェスが得られます。 複数のデータ ポイントが近接している部分では、傾斜 (一次導関数) が急激に変化する可能性があります。したがって、このモデルは二次導関数 (曲率) の推定には適していません。
[スプライン (Spline)] ツールの [加重] 引数を値 0 にすることによって、基本的な内挿手法を適用できます。
スプラインの種類
スプラインの種類には「レギュラー」と「テンション」の 2 つがあります。 レギュラー タイプはスムーズで徐々に変化するサーフェスを作成し、サンプル データの範囲外の値をとることができます。 テンション タイプはモデル化する現象の特性に合わせて、サーフェスの剛性を制御します。 作成するサーフェスはレギュラー法よりもスムーズでなく、値はサンプル データ範囲により一層密接に制限されます。
レギュラー スプライン
[レギュラー] オプションを指定すると最小化条件が変更され、三次導関数項が最小化条件に組み込まれます。 [加重] パラメーターは、最小化時に三次導関数項に付加する加重を指定し、τ(タウ) で表されます。 この項の値が大きいほど、サーフェスが滑らかになります。 適切な値は 0 ～ 0.5 です。 このオプションを使用すると、スムーズな一次導関数サーフェスにより滑らかなサーフェスが得られます。 内挿サーフェスの二次導関数を求める必要がある場合に、この手法が役立ちます。
テンション スプライン
[テンション] オプションを指定すると最小化条件が変更され、一次導関数項が最小化条件に組み込まれます。 [加重] パラメーターは、最小化時に一次導関数項に付加する加重を指定し、φ (ファイ) で表されます。 加重をゼロにすると、基本的な薄板スプライン補間が適用されます。 加重が大きいほど薄板の剛性が小さくなり、ファイを無限に大きくすると、サーフェスは、指定したポイントを通過する薄膜 (ゴム シート) の形状に近づきます。 内挿されたサーフェスは滑らかです。 一次導関数は連続性がありますが、滑らかではありません。
その他のスプライン パラメーター
出力サーフェスの細かな制御は、加重とポイント数の 2 つの追加パラメーターにより行います。
加重パラメーター
レギュラー スプライン法の場合、[加重] パラメーターは、曲率最小化式におけるサーフェスの三次導関数の加重を定義します。 加重が大きくなるほど、出力サーフェスが滑らかになります。 このパラメーターに入力する値は、0 以上である必要があります。 使用される代表的な値は、0、0.001、0.01、0.1、および 0.5 です。
テンション スプライン法の場合、[加重] パラメーターは張力の加重を定義します。 加重が大きくなるほど、出力サーフェスが粗くなります。 入力する値は、0 以上である必要があります。 代表的な値は、0、1、5、および 10 です。
ポイント数パラメーター
[ポイント数] は、内挿する各セルの計算に使用するポイント数です。 指定する入力ポイント数が多いほど、離れたポイントから各セルが受ける影響が大きくなり、出力サーフェスが滑らかになります。 ポイント数が多くなるほど、出力ラスターの処理時間が長くなります。
スプラインの数式
スプライン ツールでは、次の数式を使用してサーフェスが内挿されます。
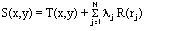
- ここで、
j = 1, 2, ..., N
N = ポイント数
λj = 一次方程式の解に基づく係数
rj = ポイント (x,y) から jth ポイントまでの距離
T(x,y) と R(r) は、選択したオプションによって異なります。
計算時には、出力ラスター全体が、サイズの等しい複数のブロックまたは領域に分割されます。 X 方向と Y 方向の領域数は同じであり、領域の形状は四角形です。 その際、「入力ポイント データセットの合計ポイント数」÷「指定したポイント数」が領域数となります。 分布が均一でないデータの場合、各領域のポイント数が大きく異なる可能性があり、ポイント数パラメーターの値はあくまでおよその平均となります。 領域のポイント数が 8 個に満たない場合、その領域は、少なくとも 8 個のポイントが含まれるように拡張されます。
レギュラー オプションについて
T(x,y) = a1 + a2x + a3y- ここで、
ai = 一次方程式の解に基づく係数
および
- ここで、
r = ポイントとサンプル間の距離
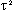= [加重] パラメーターKo = 変形ベッセル関数
c = 定数 0.577215
テンション オプションについて
T(x,y) = a1- ここで、
a1 = 一次方程式の解に基づく係数
および
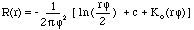
- ここで、
r = ポイントとサンプル間の距離
φ2 = [加重] パラメーター
Ko = 変形ベッセル関数
c = 定数 0.577215
出力時の領域処理
計算時には、出力ラスター全体が、サイズの等しい複数のブロックまたは領域に分割されます。 X 方向と Y 方向の領域数は同じであり、領域の形状は四角形です。 その際、「入力ポイント データセットの合計ポイント数」÷「指定したポイント数」が領域数となります。 分布が均一でないデータの場合、各領域のポイント数が大きく異なる可能性があり、ポイント数パラメーターの値はあくまでおよその平均となります。 ポイント数が 8 個に満たない領域がある場合、その領域は、少なくとも 8 個のポイントが含まれるように拡張されます。
参考文献
Franke, R. 1982. Smooth Interpolation of Scattered Data by Local Thin Plate Splines. Computer and Mathematics with Applications. Vol. 8. No. 4. pp. 273–281. Great Britain.
Mitas, L., and H. Mitasova. 1988. General Variational Approach to the Interpolation Problem. Computer and Mathematics with Applications. Vol. 16. No. 12. pp. 983-992. Great Britain.