Доступно с лицензией Spatial Analyst.
Доступно с лицензией 3D Analyst.
Инструмент Сплайн использует метод интерполяции, который оценивает значения, используя математические функции, которые сводят к минимуму суммарное значение кривизны, что приводит к построению сглаженной поверхности, которая проходит точно через входные точки.
Основы алгоритма
Концептуально, опорные точки вытягиваются на высоту их величины. Сплайн строит поверхность по принципу резинового листа, который проходит через входные точки таким образом, чтобы суммарная кривизна поверхности была минимальна. Математическая функция обрабатывает заданное количество ближайших входных точек при прохождении через опорные точки. Этот метод лучше всего подходит для несильно меняющихся поверхностей, например, рельефа, высот грунтовых вод или концентрации загрязняющих веществ.
Основная форма интерполяции по методу Сплайна с минимальной кривизной накладывает на интерполятор два основных условия:
- Поверхность должна проходить точно через точки с данными.
- Поверхность должна обладать минимальной кривизной. Накопленная сумма квадратов вторых производных поверхности, взятых для каждой точки поверхности, должна быть минимальной.
Базовая методика минимальной кривизны также рассматривается как интерполяция по методу тонкостенной плиты. Она обеспечивает построение сглаженной (непрерывной и дифференцируемой) поверхности, наряду с непрерывными поверхностями первой производной. Быстрые изменения в градиенте или уклоне (первая производная) могут произойти по соседству с опорными точками; следовательно, эта модель не подходит для оценки второй производной (кривизны).
Базовая методика интерполяции может быть применена при использовании нулевого значения для аргумента Вес к инструменту Сплайн.
Типы сплайна
Используется два типа построения сплайнов: Регулязированный и С натяжением. Регуляризованный тип создает сглаженную, постепенно меняющуюся поверхность со значениями, которые могут выходить за пределы диапазона опорных точек. Тип С натяжением контролирует жесткость поверхности в соответствии с характером моделируемого явления. Он создаёт менее сглаженную поверхность со значениями, более тесно ограниченными диапазоном опорных данных.
Тип сплайна Регуляризованный
Опция Регуляризованный меняет критерии минимизации таким образом, что в эти критерии включается третья производная. Параметр Вес задаёт вес, присвоенный третьей производной во время минимизации; этот вес в литературе носит название τ (тау). Высокие значения этого параметра приводят к построению более сглаженной поверхности. Подходят значения от 0 до 0,5. Хорошо подходят значения от 0 до 0.5. Использование этой опции обеспечивает построение сглаженной поверхности, наряду со сглаженными поверхностями первой производной. Эта методика полезна в тех случаях, когда необходимо вычислить вторую производную проинтерполированной поверхности.
Тип сплайна С натяжением
Опция С натяжением модифицирует критерии минимизации таким образом, что в критерии минимизации включаются элементы первой производной. Параметр Вес задаёт вес, присвоенный элементам первой производной в процессе минимизации; этот вес в литературе носит название Φ (фи). Нулевое значение веса приводит к использованию базовой Сплайн-интерполяции по методу тонкостенной плиты. Использование более высокого значения веса уменьшает жесткость плиты, и в пределе, по мере того, как фи стремится к бесконечности, поверхность приближается по форме к мембране или резиновым листам, проходящим через опорные точки. Проинтерполированная поверхность является сглаженной. Первые производные непрерывны, но не сглажены.
Дополнительные параметры сплайна
Дальнейший контроль за выходной поверхностью осуществляется с помощью двух дополнительных параметров: вес и число точек.
Параметр Вес
Для метода сплайна Регуляризованный параметр Вес определяет вес третьих производных поверхности в выражении минимизации кривизны. Чем больше вес, тем более сглажена выходная поверхность. Значения, введенные для этого параметра, должны быть больше или равны нулю. Обычно используются значения 0, 0,001, 0,01, 0,1 и 0,5.
Для метода сплайна С натяжением параметр Вес определяет вес натяжения. Чем больше вес, тем более грубая выходная поверхность. Введенные значения должны быть больше или равны нулю. Обычно используются значения 0, 1, 5 и 10.
Параметр Число точек
Параметр Число точек определяет количество точек, используемых в вычислении каждой интерполируемой ячейки. Чем больше входных точек вы зададите, тем больше на каждую ячейку будут влиять отдаленные точки и тем более сглаженной будет выходная поверхность. Чем больше количество точек, тем больше времени займет обработка выходного растра.
Уравнение сплайна
Алгоритм, используемый для инструмента Сплайн использует следующую формулу для интерполяции поверхности:
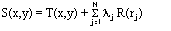
- где:
j = 1, 2, ..., N.
N – количество точек.
λj коэффициенты, найденные на основании решения системы линейных уравнений.
rj это расстояние из точки (x,y) в точку j.
T(x,y) и R(r) определяются по-разному, в зависимости от выбранной опции.
Для вычислительных целей все пространство выходного растра делится на блоки или регионы, равные по размеру. Число регионов по направлениям x и y одинаково, они имеют форму прямоугольника. Число регионов определяется путём деления общего количества точек во входном наборе точек на число, заданное для числа точек. Для менее равномерно распределенных данных регионы могут содержать значительно различающееся количество точек, при этом количество точек является только грубым средним. Если в одном любом из регионов число точек меньше восьми, регион будет расширен до того размера, при котором в него попадут минимум восемь точек.
Для опции Регуляризованный
T(x,y) = a1 + a2x + a3y- где:
ai коэффициенты, полученные в результате решения системы линейных уравнений.
и
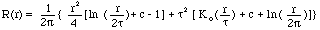
- где:
r расстояние между искомой и опорной точкой.
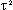– параметр Вес.Ko модифицированная функция Бесселя.
c константа, равная 0,577215.
Для опции С натяжением
T(x,y) = a1- где:
a1 коэффициент, полученный в результате решения системы линейных уравнений.
и
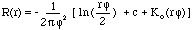
- где:
r расстояние между искомой и опорной точкой.
φ2 параметр Вес.
Ko модифицированная функция Бесселя.
c константа, равная 0,577215.
Региональная обработка выходных данных
Для вычислительных целей все пространство выходного растра делится на блоки или регионы, равные по размеру. Число регионов по направлениям x и y одинаково, они имеют форму прямоугольника. Число регионов определяется путём деления общего количества точек во входном наборе точек на число, заданное для числа точек. Для менее равномерно распределенных данных регионы могут содержать значительно различающееся количество точек, при этом количество точек является только грубым средним. Если в одном любом из регионов число точек меньше восьми, регион расширяется до того размера, при котором в него попадут минимум восемь точек.
Справочная информация
Франке Р. (Franke, R.) 1982. Сглаженная интерполяция дискретных данных локальными сплайнами. Журнал "Computer and Mathematics with Applications". Vol. 8. No. 4. pp. 273–281. Great Britain.
Митас Л., Митасова Х. (Mitas, L., H. Mitasova.) Вариационный подход к проблеме интерполяции. Журнал "Computer and Mathematics with Applications". Vol. 16. No. 12. pp. 983-992. Great Britain.