Как работает инструмент Локальные бивариантные отношения

Важнейший компонент множества рабочих процессов ГИС-анализа – сравнение двух переменных в области изучения, чтобы определить, связаны ли они между собой, и как проявляется эта связь. Например, есть ли связь между диабетом и ожирением в конкретной области? Исторически, для получения ответа на вопрос такого типа надо было либо выполнить картографическое сравнение, либо анализ линейной регрессии. Картографическое сравнение может быть субъективным, а регрессионный анализ может выявить только простые отношения.

Инструмент Локальные бивариантные отношения позволяет оценить отношения между двумя переменными на одной карте, определив, зависимы ли значения одной переменной на значения другой (влияет ли одна переменная на другую), и меняются ли эти отношения в географическом пространстве. Инструмент вычисляет статистику энтропии в каждой локальной окрестности, которая количественно оценивает объем совместной для двух переменных информации. В отличие от других типов статистики, которые часто могут идентифицировать только линейные отношения (в частности, линейную регрессию), статистика энтропии может выявить любую структуру отношений между переменными, включая экспоненциальную, квадратическую, синусоидальную и даже сложные отношения, которые не описываются типовыми математическими функциями. Этот инструмент использует точки или полигоны в качестве входных данных и создает выходной класс объектов, в котором суммируются значимость и форма отношений каждого входного объекта. Кроме того, инструмент возвращает настраиваемые всплывающие окна и разнообразные диагностики, диаграммы и сообщения.

Возможное применение

Этот инструмент можно использовать для следующих типов приложений:

• Центр контроля и профилактики заболеваемости (CDC) утверждает: "Люди с ожирением, в сравнении с людьми с нормальным (здоровым) весом, в значительно большей степени подвержены риску ряда серьезных заболеваний, включая диабет 2го типа". CDC может использовать этот инструмент для оценки интенсивности отношений между ожирением и диабетом, а также оценить, насколько постоянны такие отношения по всей области изучения.
• Сотрудники здравоохранения могут изучать отношения между уровнем загрязнения воздуха и социально-экономическими факторами для выявления возможной социальной несправедливости.

Метод энтропии

Что значит для двух переменных - быть связанными друг с другом? Есть множество типов отношений между переменными, но, в простейшем смысле, две переменные связаны, если информацию об одной переменной можно узнать, оценивая значения другой переменной. Например, можно узнать о степени риска заболевания диабетом, изучая информацию о распространении ожирения. Это называется зависимостью между двумя переменными, и, наоборот, если никакая информация об одной переменной не может быть получена путем изучения другой переменной, то такие переменные называются независимыми.

Один из способов измерения степени отношений между переменными ­ использовать энтропию. Энтропия - фундаментальная основа теории информации, и используется для оценки доли неопределенности в случайной переменной. В целом, чем меньше прогнозируема переменная, тем выше энтропия. Вычисление энтропии широко применяется. Она может быть рассчитана для отдельных случайных переменных, а сочлененная энтропия может быть рассчитана между двумя или более переменными. Сочлененная энтропия двух переменных равна энтропии первой переменной плюс энтропии второй переменной, и минус взаимная информация двух переменных. Взаимная информация служит важной количественной оценкой уровня зависимости между переменными, так как она напрямую сообщает, сколько информации об одной переменной можно получить, изучая значения другой переменной.

Чтобы оценить взаимную информацию, необходимо оценить энтропию каждой отдельной переменной и их общую энтропию. Но эти значения зависят от базового распределения переменных и почти никогда не известны на практике. К счастью, последние исследования показали, что для оценки общей, совместной энтропии нескольких переменных можно использовать взвешенные возможности дерева с минимальным охватом в качестве замены совместного распределения этих переменных (Guo, 2010). Это позволит получить оценку сочлененной энтропии без необходимости отдельно рассчитывать распределения для каждой переменной. Возможность оценить совместную энтропию полезна сама по себе, но в реальности нам необходимо знать взаимную информацию между переменными для того, чтобы определить, являются ли эти две переменные связанными. Так как мы не можем напрямую оценить взаимную информацию, не зная распределения этих двух переменных, по прежнему можно использовать перестановки для построения теста нулевой гипотезы для статистически значимых отношений.

Тестирование значимости отношений с помощью перестановок

Как описано в предыдущем разделе, вопрос о том, связаны ли две переменные, эквивалентен вопросу будет ли сочлененная энтропия (которую можно оценить) существенно меньше, чем сумма отдельных энтропий двух переменных (которые не могу быть оценены). Другими словами, будет ли оцененная сочлененная энтропия данных существенно меньше, чем она была бы, если две переменные были независимы?

Чтобы подтвердить или опровергнуть это определение, с переменными выполняются перестановки, случайным образом заменяющие каждое значение первой переменной новым значением второй переменной. Поскольку пары подбираются случайно, наборы данных, в которых произведена перестановка, не будут обмениваться взаимной информацией, но отдельные энтропии двух переменных при этом не изменятся. Генерируя множество наборов данных с перестановками и оценивая совместную энтропию каждого набора, мы можем построить распределение совместной энтропии с нулевой гипотезой, что обе переменные независимы и не связаны. Сочлененная энтропия, оцениваемая для актуальных данных, затем сравнивается с их распределениями, и вычисляется псевдо p-значение, исходя из доли перестановок, которые приводят к получению сочлененной энтропии меньше, чем сочлененная энтропия актуальных данных.

Тест на наличие локальных пространственных отношений

Описанная выше процедура оценки значимости отношений между двумя переменными может быть применена к любым непрерывным бивариантным данным. Чтобы применить такую процедуру для тестирования локальных пространственных отношений, тест нулевой гипотезы выполняется для каждого входного объекта, с определением ближайшей окрестности. Это позволит вам визуализировать результаты на карте и идентифицировать локальные области, где между переменными присутствуют выраженные отношения.

Все значения параметров Зависимой переменной и Независимой переменной сначала переклассифицируются в диапазон от 0 до 1, путем вычитания минимального значения всего набора данных и деления на диапазон (максимум минус минимум) всего набора. Затем для каждого входного объекта выполняются следующие действия:

1. Определяются объекты в ближайшей окрестности (соседи). Параметр Число соседей указывает, сколько соседних объектов можно идентифицировать. Входной объект считается соседним самому себе.
2. Значения двух переклассифицированных переменных в ближайшей окрестности объединяются в один набор данных.
3. Строится минимальное остовое дерево и оценивается сочлененная энтропия.
4. Выполнятся случайные перестановки значений и оценивается сочлененная энтропия для каждой перестановки. Параметр Число перестановок указывает, сколько перестановок можно выполнить.
5. Вычисляется псевдо p-значение и определяется статистическая значимость отношения.

Поскольку в этой процедуре выполняются разные проверки гипотезы для каждого входного объекта, вы можете использовать параметр Применить коррекцию средней доли ложных отклонений гипотезы (FDR) для оценки доли ложно положительных результатов (ошибки 1-го типа).

Классификация локальных отношений

Очень важно определить области, где две переменные имеют статистически значимые отношения. Для использования этой информации желательно определить тип отношений между этими переменными на основе того, насколько хорошо независимая переменная может предвидеть значение зависимой переменной.

Каждому объекту присваивается одна из следующих категорий отношений:

• Не значимы – между переменными не выявлено статистически значимых отношений.
• Линейные положительные – зависимая переменная линейно возрастает с ростом независимой переменной.
• Линейные отрицательные - зависимая переменная линейно снижается с ростом независимой переменной.
• Вогнутые - зависимая переменная изменяется, образуя вогнутую кривую с ростом независимой переменной. Вогнутые кривые изогнуты дугой вниз.
• Выпуклые – зависимая переменная изменяется, образуя выпуклую кривую с ростом независимой переменной. Выпуклые кривые изогнуты дугой вверх.
• Сложные неопределенные – переменные значимо связаны, но тип отношений не может быть корректно описан какой-либо категорией.

Ниже показаны некоторые примеры Вогнутых отношений.

Здесь показаны типовые примеры вогнутых отношений между двумя переменными.

Ниже показаны некоторые примеры Выпуклых отношений.

Здесь показаны типовые примеры выпуклых отношений между двумя переменными.

Выполните следующие шаги для классификации всех значимых объектов:

1. Оценка простой модели линейной регрессии для прогнозирования значений зависимой переменной на основе значений независимой переменной и вычисление Скорректированного информационного критерия Акаике (AICc) для модели.
2. Оценка модели линейной регрессии второго порядка для прогнозирования значений зависимой переменной на основе значений независимой переменной и квадратов значений независимой переменной (квадратическая модель регрессии), и вычисление критерия AICc.
3. Сравните значения AICc для двух моделей регрессии и выберите ту, которая лучше описывает это отношение. Для выбора квадратической модели AICc квадратической модели регрессии должен быть по крайней мере на 3 меньше, чем AICc модели линейной регрессии. В обратном случае предпочтительнее линейная модель.
4. Вычисление скорректированного значения R² для выбранной модели. Если это значение меньше 0,05, значит, выбранная модель объясняет менее 5 процентов вариантов данных, и отношения классифицируются как Сложные неопределенные.
5. Если скорректированный R² больше, чем 0,05, классификация выполняется по следующим правилам:
   • Если была выбрана линейная модель, и коэффициент положительный, отношения классифицируются как Линейные положительные.
   • Если была выбрана линейная модель, и коэффициент отрицательный, отношения классифицируются Линейная отрицательные .
   • Если была выбрана квадратическая модель, и коэффициент квадратного члена положительный, отношения классифицируются как Выпуклые.
   • Если была выбрана квадратическая модель, и коэффициент квадратного члена отрицательный, отношения классифицируются как Вогнутые.

Интерпретация результатов

Выходными данными этого инструмента является класс объектов с символами по типам отношений и сводные статистические данные, выведенные в сообщениях геообработки. Выходные объекты содержат информационные поля, а также всплывающие окна, в которых отношение визуализируется с помощью точечных диаграмм.

Всплывающие окна с точечными диаграммами

Если указано, для каждого выходного объекта создаются всплывающие окна с точечными диаграммами, которые можно увидеть, щелкнув объект на карте. На следующем рисунке показано всплывающее окно с точечной диаграммой для объекта с положительным линейным отношением:

Здесь показано всплывающее окно с точечной диаграммой для положительного линейного отношения.

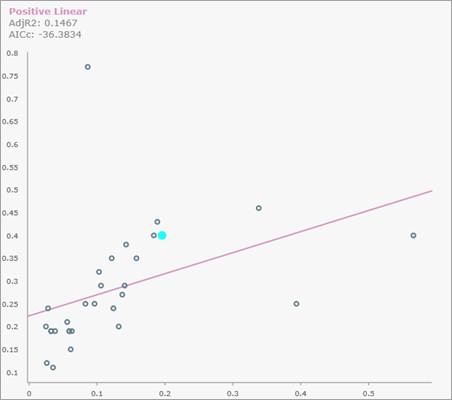
Нормированные значения переклассифицированной независимой переменной откладываются по оси x, а переклассифицированной зависимой – по оси y. Подсвеченная точка на точечной диаграмме соответствует самому объекту; все остальные точки представляют соседние объекты в ближайшей окрестности.

Если навести указатель мыши на точку на точечной диаграмме, можно увидеть Source ID объекта и переклассифицированные значения зависимых и независимых переменных, а также их необработанные (по исходной шкале) значения в круглых скобках.

Сообщения геообработки

Сводная информация о статистической значимости и типах отношений отображается в виде сообщений геообработки. Пример таких сообщений приведен ниже.

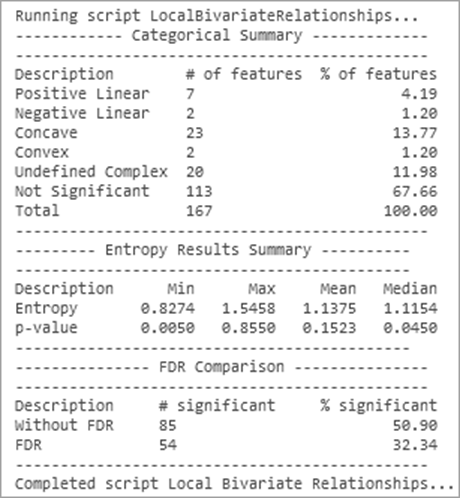
В разделе Категорийная сводка приводится количество объектов и доли в процентах для каждого типа отношений. В разделе Итоговая сводка энтропии перечислены минимальное, максимальное, среднее и медианное значения энтропии и p-значения входных объектов. В разделах Сравнение FDR приводится количество и процент статистически значимых отношений с применением и без применения коррекции средней доли ложных отклонений.

Примечание:

Сообщения геообработки отображаются в нижней части панели Геообработка в процессе выполнения инструмента. Вы также можете получить доступ к сообщениям при помощи Истории геообработки остановив курсор мыши над индикатором выполнения и щелкнув на всплывающей кнопке либо развернув раздел сообщений на панели Геообработка.

Выходные поля

Выходные данные этого инструмента содержат различные поля, которые содержат информацию о том, к какой категории типа отношений был отнесен тот или иной объект и почему.

Значимость отношений

Следующие поля содержат информацию о том, является ли отношение между зависимой и независимой переменными статистически значимым:

• Entropy – Ожидаемое значение энтропии объекта.
• P-values – Псевдо p-значение теста на значимое отношение между зависимой и независимой переменными. Это значение не подлежит коррекции на величину средней доли ложных отклонений.
• Local Bivariate Relationship Confidence Level – Наивысший уровень уверенности, который является удовлетворительным для данного объекта. Для этого поля возможны следующие значения: 90% уверенность, 95% уверенность, 99% уверенность и Не значимы. Если задано значение параметра Применить коррекцию средней доли ложных отклонений гипотезы (FDR), уровень уверенности корректируется на величину средней доли ложных отклонений.

Классификация отношений

Следующие поля содержат информацию о классификации типа отношений между зависимой и независимой переменными:

• Type of Relationship – Тип отношения между зависимой и независимой переменными
• AICc (Linear) – Скорректированный Информационный критерий Акаике для линейной модели
• R-squared (Linear) – Значение R² для линейной модели
• AICc (Polynomial) – Скорректированный Информационный критерий Акаике для полиномиальной модели
• R-squared (Polynomial) – Значение R² для полиномиальной модели

Примечание:

Значения AICc и R² для объектов, не имеющих статистически значимых отношений между зависимой и независимой переменными, будут нулевыми.

Коэффициенты регрессии и значимость

Следующие поля предоставляют информацию о коэффициентах линейных и полиномиальных моделей, которые используются для классификации отношения:

• Intercept – Отрезок прямой линейной модели.
• Coefficient (Linear) – Коэффициент линейного члена линейной модели.
• Polynomial Intercept – Отрезок прямой полиномиальной модели.
• Polynomial Coefficient (Linear) – Коэффициент линейного члена полиномиальной модели.
• Polynomial Intercept (Squared) – Коэффициент квадратного члена полиномиальной модели.
• Significance of Coefficients (Linear) – Двухзначный код, указывающий, являются ли отрезок прямой и коэффициент статистически значимыми при уровне уверенности 90 процентов. Нижнее подчеркивание (_) указывает на то, что значение не является статистически значимым, а звездочка (*) – что значение статистически значимое. Например, сочетание *_ говорит о том, что отрезок прямой является статистически значимым, а линейный коэффициент таковым не является. И наоборот, сочетание _* указывает, что отрезок прямой не является статистически значимым, а линейный коэффициент таковым является.
• Significance of Coefficients (Polynomial) – Трехзначный код, указывающий, являются ли отрезок прямой, линейный коэффициент и квадратный коэффициент полиномиальной модели статистически значимыми при уровне уверенности 90 процентов. Например, *_* указывает на то, что отрезок прямой является статистически значимым, линейный коэффициент не является статистически значимым, а квадратный коэффициент таковым является.

Примечание:

Все поля, связанные с коэффициентами регрессии, будут нулевыми или пустыми строками для каждого объекта, который не имеет статистически значимых отношений между зависимыми и независимыми переменными.

Подсказки

При использовании инструмента Локальные бивариантные отношения примите во внимание следующие советы:

• Используйте параметр Коэффициент масштабирования для настройки чувствительности инструмента к трудноуловимым отношениям. Если значение коэффициент масштабирования приближается к 0, будут идентифицироваться только четко выраженные отношения, а значение ближе к 1 позволит дополнительно выявить слабо выраженные выраженные отношения. Значение по умолчанию – 0.5 – позволит идентифицировать сильно и средне выраженные отношения.
• Логика выбираемого значения для параметра Количество соседей неоднозначна. Использование большего числа соседей дает больше данных для тестирования каждой гипотезы, что увеличивает вероятность обнаружения значимой связи. Но в то же время, чем большее число соседей будет использоваться, тем менее локальным будет тестирование, поскольку в этом случае поиск соседей будет выполняться на большем расстоянии, и локальные отношения могут не обнаружиться. Большое число соседей также быстро увеличивает время работы инструмента.
• Выбор значения параметра Число перестановок является компромиссом между точностью и временем обработки. Увеличение числа перестановок повышает точность, поскольку увеличивается диапазон возможных значений для вычисления псевдо p. Например, с 99 перестановками, точность псевдо p-значения составляет .01, а для 999 перестановок, точность равна .001. Эти значения вычисляются путем деления 1 на количество перестановок плюс один: 1/(1+99) и 1/(1+999). Малое число перестановок может использоваться для начального изучения проблемы, но для получения окончательного результата рекомендуется увеличить количество перестановок до максимально возможного. Также рекомендуется увеличивать количество перестановок при использовании большего числа соседей.

Ссылка

• Guo, D. "Local entropy map: a nonparametric approach to detecting spatially varying multivariate relationships." International Journal of Geographical Information Science 24, no. 9 (2010): 1367-1389.