Как определяется расстояние
Расстояние между любыми двумя объектами вычисляется как минимальный интервал между ними, т.е., там, где два объекта расположены ближе всего друг к другу. Эта логика действует во всех инструментах геообработки, которые вычисляют расстояние, включая такие инструменты, как Ближайший объект, Построить таблицу ближайших объектов и Пространственное соединение (с опцией ближайших совпадений).
Измерения расстояний имеют наибольшую точность, если входные данные используют систему координат равнопромежуточной проекции. Хотя вычисление расстояния может быть выполнено независимо от системы координат, результат может оказаться не точным или даже бессмысленным, если данные используют географическую систему координат или система координат задана неправильно.
Более подробно о картографических проекциях и системах координат
Для дальнейшего обсуждения, расстоянием всегда будет считаться минимальный интервал между двумя объектами.
Особые соображения
- Несколько объектов могут оказаться на одинаковом удалении от другого объекта. В таком случае один из равноудаленных объектов будет выбираться в качестве ближайшего случайным образом.
- Если один из объектов содержит другой или находится внутри другого объекта, расстояние между ними равно 0.
- Это означает, что если объект находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
- Расстояние между двумя объектами равняется нулю всякий раз, когда у них имеется хотя бы одна общая координата x,y.
- Это означает, что при пересечении, перекрытии или касании двух объектов, расстояние между ними равняется 0.
- Расстояние всегда вычисляется до границы полигонального объекта, не до центра или центроида полигона.
- Как отмечено выше, если объект полностью находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
- Расстояние между двумя объектами (любого типа) не меняется в зависимости от направления измерения.
Основные операции для определения расстояния
Вычисление расстояния зависит от типа геометрии объектов, а также от других факторов, таких как система координат. Однако есть три основных правила, подробнее описанные ниже, которые определяют способ вычисления расстояния.
- Расстояние между двумя точками является прямой линией, соединяющей их.
- Расстояние от точки до линии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины.
- Расстояние между полилиниями определяется вершинами сегментов.
Правило 1: расстояние между двумя точками является прямой линией, соединяющей их
На рисунке ниже показано расстояние между двумя точками, вместе с несколькими ключевыми словами и объектами, использующимися инструментами близости.
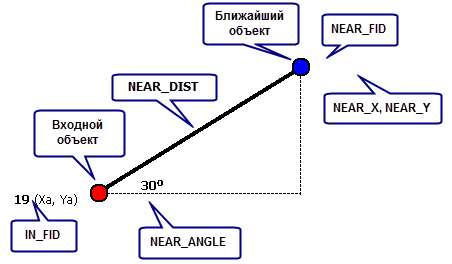
Ключевые слова в вышеуказанных выносках (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) являются полями, добавляемыми к выходным данным инструментами Построить таблицу ближайших объектов и , а также к входному классу объектов при использовании инструмента Ближайший объект.
Расстояние между мультиточками
Для особого случая, когда определяется расстояние между мультиточками, вычисляются расстояния от каждой точки входного мультиточечного объекта до каждой точки ближайшего мультиточечного объекта с помощью Правила 1, минимальное из этих трех расстояний станет расстоянием между мультиточечными объектами.
Кроме того, когда одна из точек мультиточечного объекта находится поверх одной из точек другого мультиточечного объекта, расстояние между ними равняется 0. Это справедливо для всех составных объектов.
Правило 2: расстояние от точки до полилинии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины
В ArcGIS линейные объекты называются полилиниями. Эти два термина, линия и полилиния, взаимозаменяемы. Полилиния является упорядоченным набором точек, эти точки называются вершинами. An individual vertice is a vertex. Полилиния может иметь любое количество вершин. Линия, заданная двумя вершинами, называется сегментом. Две вершины, которые задают сегмент линии, называются конечными вершинами.
Сходным образом, полигон является замкнутой областью, заданной одной или несколькими полилиниями.
Кратчайшим расстоянием от точки до сегмента линии является перпендикуляр к ней. Если в пределах конечных вершин сегмента перпендикуляр провести не удается, кратчайшим расстоянием будет расстояние до ближайшей конечной вершины.
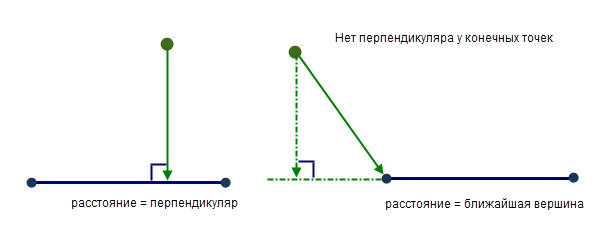
Расстояние от точки до полилинии
Если полилиния содержит только один сегмент, для вычисления расстояния применяется Правило 2.
Если полилиния состоит из нескольких сегментов (чаще всего), сначала определяется ближайший к точке сегмент линии, затем для вычисления расстояния применяется Правило 2.
Расстояние от точки до полигона
Поскольку полигон является замкнутой областью, образованной набором сегментов линий, вычисление расстояния от точки до полигона включает определение ближайшего к точке сегмента, затем применяется Правило 2.
Расстояние будет определяться, только если точка находится вне полигона; иначе, расстояние равно 0.
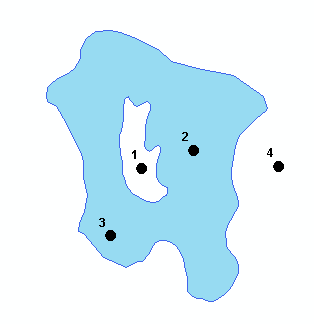
На рисунке выше, для точек 2 и 3 расстояние равно 0, для точек 1 и 4 – расстояние положительно.
Правило 3: расстояние между полилиниями определяется вершинами сегментов линии
Для двух объектов, не являющихся точками, таких как два сегмента линий:
- Расстояние вычисляется от каждой из конечных вершин входного сегмента до ближайшего сегмента с использованием Правила 2.
- Расстояние вычисляется от каждой из конечных вершин ближайшего сегмента до входного сегмента.
Расстояние от полилинии до полилинии
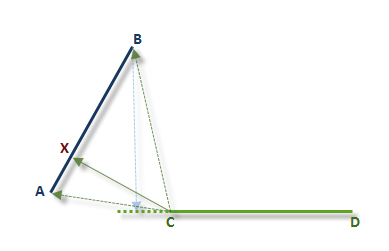
В простейшем случае, предположим, что оба полилинейных объекта состоят из одного сегмента. На рисунке ниже показан перпендикуляр CX от вершины C до сегмента, заданного вершинами AB. Перпендикуляр от вершины D также вычисляется, но это расстояние больше, чем расстояние CX. Поэтому CX является кратчайшим расстоянием от сегмента CD до сегмента AB.
Обратите внимание, что перпендикуляр от вершины A или B до сегмента CD провести нельзя, поэтому, кратчайшее расстояние вычисляется от вершин A и B до вершины C. В результате, именно AC является кратчайшим расстоянием между сегментами AB и CD.
Из двух вычисленных расстояний (AC и CX), CX является кратчайшим между двумя сегментами, поскольку это минимальное расстояние из всех расстояний между вершинами и сегментом.
Когда обе полилинии состоят из нескольких сегментов, определяются два наиболее близкорасположенных друг к другу сегмента, затем вычисляется расстояние, согласно Правилу 3.
Расстояние от полилинии до полигона
При вычислении расстояния между полилинией и полигоном определяются два наиболее близкорасположенных сегмента: один сегмент полилинии и один сегмент из образующих границу полигона. Расстояние между этими двумя сегментами определяется так же, как описано в Правиле 3.
Краткая информация
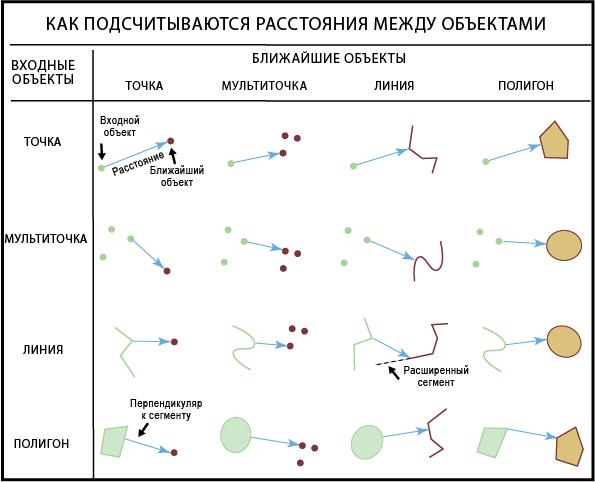
На следующем рисунке показано, как измеряется расстояние между объектами различных типов и определяется положение ближайших объектов. Показаны не все возможные комбинации.