Агрегация случайных точечных данных в регулярные сетки используется по многим причинам, в частности для нормирования географии для нанесения на карту или для уменьшения неоднородности при использовании полигонов неправильной формы, созданных произвольно (например, границы избирательных округов или блоков, созданных в результате политических процессов). Регулярные сетки могут состоять только из равносторонних треугольников, квадратов или шестиугольников, т.к. только такая геометрия полигонов позволяет создавать мозаичное замощение (совокупность одинаковых фигур, охватывающую всю область без пробелов и перекрытий), чтобы получить равномерную сетку.

Хотя сетка квадратов является основным типом геометрии в ГИС-анализе и тематической картографии, бывают ситуации, когда шестиугольники лучше подходят для анализа, в зависимости от сути вопроса.
Агрегация по гексагональной сетке может применять по следующим причинам:
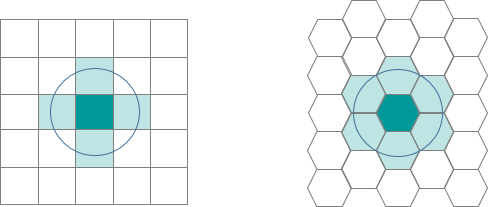
- Шестиугольники позволяют уменьшить смещение выборки из-за краевых эффектов, вызванных геометрией сетки, что связано с низким значением соотношения периметра к площади шестиугольника. Наименьшее соотношение имеет окружность, но окружности не могут создать замощение в виде непрерывной сетки. Шестиугольники обладают наиболее близкой к окружности геометрией и могут складываться в мозаику, формируя равномерную сетку.
- Такая приближенность гексагональной сетки к окружности позволяет более естественно представлять кривые в распределении данных, чем квадратная сетка.
- При сравнении полигонов с равными площадями, чем ближе форма полигона к окружности, тем ближе к центроиду оказываются точки у границ (особенно рядом с вершинами). Это означает, что любая точка внутри шестиугольника находится ближе к его центроиду, чем любая точка в квадрате или треугольнике равной площади (из-за более острых углов квадрата и треугольника по сравнению с шестиугольником).
- Шестиугольники более предпочтительны, когда в анализ включаются аспекты связности или пути перемещения.
- Из-за линейной природы прямоугольников, регулярные сетки формируют прямые параллельные линии, что может скрывать от наблюдателя закономерности, имеющиеся в данных. Шестиугольники позволяют разбить эти линии и позволяют легче наблюдать закономерности в данных, имеющие криволинейную форму. Это позволяет прервать искусственные прямолинейные закономерности и снизить смещение по расположению, которое может проявляться в регулярных сетках.
- Если вы работаете с большой областью, гексагональная сетка вносит меньше искажений, вызванных кривизной земной поверхности, чем регулярная сетка.
- Поиск соседств с помощью гексагональной сетки является более эффективным. Поскольку ребро или длина контакта каждой стороны одинаковы, центроид каждого соседства является равноудаленным. Однако с регулярной сеткой центроиды соседства Queen's Case (над/под/справа/слева) находятся на удалении N единиц, а центроиды диагонального (Rook) соседства – несколько дальше (точнее, на расстоянии квадратного корня из 2N единиц).
- Поскольку в гексагональной сетке расстояние между центроидами во всех шести направлениях одинаково, если вы используете для поиска соседей полосу расстояний или инструменты Оптимизированный анализ горячих точек, Оптимизированный анализ выбросов или Создать куб Пространство-Время по агрегации точек, в гексагональной сетке для каждого объекта в вычисления войдет большее число соседей, чем при использовании регулярной сетки.
Дополнительные источники:
Birch, Colin P.D., Oom, Sander P., and Beecham, Jonathan A. Rectangular and hexagonal grids used for observation, experiment, and simulation in ecology. Ecological Modelling, Vol. 206, No. 3–4. (August 2007), pp. 347–359.