Доступно с лицензией Spatial Analyst.
Различные наборы растровых данных не обязательно должны иметь одинаковый размер ячейки. Но, если вы обрабатываете несколько наборов растровых данных, желательно, чтобы размеры ячеек, а также пространственная привязка, совпадали. Когда несколько наборов растровых данных с различным разрешением загружаются в любой из инструментов дополнительного модуля ArcGIS Spatial Analyst, будет автоматически выполняться пересчет одного или нескольких наборов данных до уровня самого низкого разрешения из всех входных наборов данных.
По умолчанию, используется пересчет по методу Ближайшего соседа. Этот метод подходит и для дискретных, и для непрерывных данных, в то время как другие методы пересчета – билинейная интерполяция и кубическая свертка – подходят только для непрерывных данных. Использование различных методов пересчета необходимо, поскольку центры входных ячеек редко совпадают с центрами ячеек, полученных после изменения разрешения. Билинейную интерполяцию и кубическую свертку можно применить с помощью инструмента Изменить разрешение, в качестве предварительного шага перед комбинированием растров с различными разрешениями.
Примечание:
Некоторые инструменты, такие как инструменты из группы инструментов Поверхность, будут использовать билинейную интерполяцию, как метод интерполяции по умолчанию. Ознакомьтесь со справкой по конкретному инструменту для более подробной информации.
Разрешение пересчета по умолчанию можно контролировать параметром среды Размер ячейки, с помощью которого можно выбрать, будет ли инструмент использовать минимальное разрешение входных растров или заданный вами размер ячейки.
Примечание:
Будьте внимательны при выборе размера ячейки меньше, чем во входных наборах растровых данных. При этом детализация увеличиваться не будет, новые ячейки будут интерполированы по методу Ближайшего соседа. Точность результата соответствует точности самых грубых данных. Выбрав размер ячейки 50 метров для наборов данных, имеющих размер ячейки 100 метров, можно создать выходной растр с ячейками размером 50 метров, однако точность этого растра останется в пределах 100 метров на ячейку.
На рисунке ниже показаны ячейки, размер которых больше, чем размер ячеек входных растров. Поэтому входной набор растровых данных будет сначала пересчитан для понижения разрешения, а затем будет применен инструмент.
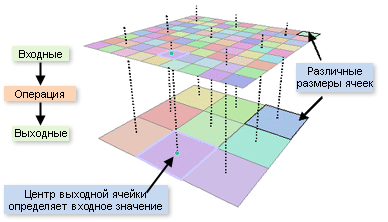
При выполнении анализа, убедитесь, что задача соответствует используемому размеру ячейки. Например, невозможно анализировать перемещение мышей, если размер ячейки составляет пять километров. Ячейки размером в пять километров больше подходят для изучения эффектов глобального потепления.
Пересчет
Для определения значения, которое должно быть присвоено ячейке пересчитанного растра, центр этой ячейки должен быть сопоставлен с системой координат исходного растра. Координаты центра каждой ячейки должны быть обратно трансформированы для определения положения точки в исходном растре. После определения входной точки, соответствующее значение, основанное на значениях ближайших ячеек входного растра, присваивается выходной ячейке. Очень редко центр выходной ячейки соответствует центру любой ячейки входного растра. Поэтому, для определения выходного значения разработана соответствующая техника, механизм работы которой основан на положении точки относительно центров ячеек входного растра и значений, связанных с этими центрами. Для определения выходных значений используются три метода пересчета – ближайший сосед, билинейная интерполяция и кубическая свертка. Каждый из этих методов по-разному вычисляет значения выходных ячеек. Поэтому, значения, присваиваемые ячейкам выходного растра, могут отличаться в зависимости от используемого метода.
Присвоение значений по методу Ближайшего соседа
Метод Ближайшего соседа – это техника пересчета, которая используется для дискретных (категорийных) данных, поскольку при этом значения входных ячеек не изменяются. После сопоставления центра ячейки выходного растра с ячейкой входного, происходит определение ближайшего центра ячейки, затем значение этой ячейки присваивается ячейке выходного растра.
При использовании метода ближайшего соседа, значения ячеек входного растра не изменяются. Если ячейка входного растра имеет значение 2, это же значение будет перенесено в выходной растр; оно никогда не будет изменено на 2.2 или 2.3. Поскольку выходные значения остаются неизменными, метод Ближайшего соседа следует использовать с номинальными или порядковыми данными, где каждое значение представляет класс, элемент или классификацию (категорийные данные, такие как типы землепользования, почв или лесов).
Предположим, выходной растр получен из входного растра, который был повернут на 45° в процессе обработки, затем был пересчитан. Для каждой выходной ячейки необходимо определить соответствующее значение, согласно входному растру. На рисунке ниже, центры ячеек входного растра показаны серыми точками. Выходные ячейки обозначены зеленым. Обработанные ячейки показаны желтым. При использовании метода Ближайшего соседа, определяются центры ячеек входного растра, расположенные ближе всего (оранжевые точки) к центрам обрабатываемых ячеек (красные точки), затем им присваивается выходное значение обрабатываемой ячейки (выделено желтым цветом). Этот процесс повторяется для каждой ячейки выходного растра. 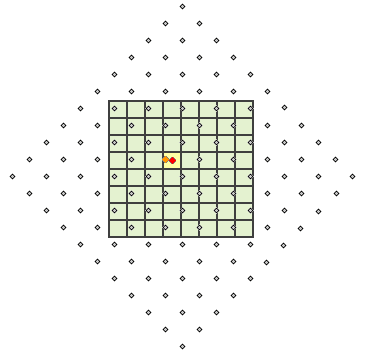
Билинейная интерполяция
При Билинейной интерполяции, для определения значения ячейки выходного растра используются значения центров четырех ближайших ячеек входного растра. Значение ячейки выходного растра вычисляется как средневзвешенное этих четырех значений, скорректированных по расстоянию от центра выходной ячейки. По сравнению с методом ближайшего соседа, этот метод пересчета позволяет получить более гладкое изображение.
На следующем рисунке, так же, как и на предыдущем, центры ячеек входного растра показаны серыми точками, выходные ячейки показаны зеленым цветом, обрабатываемые ячейки – желтым. При билинейной интерполяции, определяются четыре центра входных ячеек (оранжевые точки), расположенные ближе всего к центрам обрабатываемых ячеек (красные точки), вычисляется среднее взвешенное, затем полученное значение присваивается в качестве выходного обрабатываемой ячейке (выделено желтым). 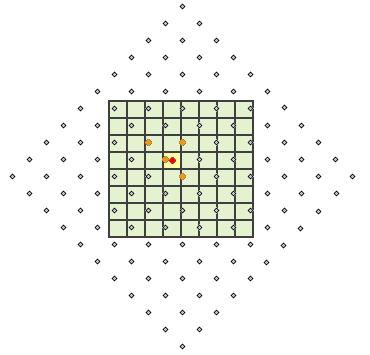
Поскольку значения выходных ячеек вычисляются в зависимости от их относительного положения и значений входных ячеек, билинейную интерполяцию лучше использовать для данных, в которых значение ячейки определяется положением относительно известной точки или явления (т.е. для непрерывных поверхностей). Высоты, уклоны, интенсивность шума аэропорта или степень солености грунтовых вод вокруг устья реки представляют собой явления, которые отображаются с помощью непрерывных поверхностей и лучше всего пересчитываются с помощью метода билинейной интерполяции.
Кубическая свертка
Кубическая свертка работает так же, как и билинейная интерполяция, за исключением того, что средневзвешенное значение вычисляется по 16 ближайшим ячейкам.
На следующем рисунке показано вычисление выходного значения при использовании кубической свертки. Определяются 16 центров входных ячеек (оранжевые точки), расположенные ближе всего к центрам обрабатываемых ячеек (красные точки), вычисляется среднее взвешенное, затем полученное значение присваивается в качестве выходного обрабатываемой ячейке (выделено желтым).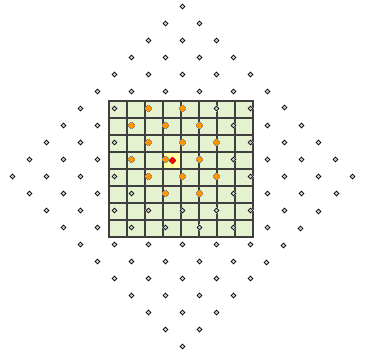
Кубическая свертка имеет тенденцию к созданию более резких границ областей данных, чем билинейная интерполяция, поскольку при вычислении выходного значения используется большее число ячеек.
Пересчет и типы данных
Билинейная интерполяция и кубическая свертка не должны использоваться с данными категорий, т.к. в выходном наборе растровых данных категории сохранены не будут. Однако все три метода можно использовать с непрерывными данными, при этом, данные полученные с помощью метода ближайшая окрестность будут иметь блочную структуру, использование билинейной интерполяции позволит получить более гладкую поверхность, а кубическая свертка – более резкую.