Доступно с лицензией Spatial Analyst.
Древовидная схема – это схема, которая показывает атрибутивные расстояния между каждой парой последовательно объединяемых классов. Чтобы избежать пересечения линий, схема графически организуется таким образом, что члены каждой пары объединяемых классов на схеме являлись соседями.
Инструмент Древовидная схема (Dendrogram) использует алгоритм иерархической кластеризации. Сначала программа вычисляет расстояния между каждой парой классов во входном файле сигнатур. Затем она итеративно объединяет ближайшие пары классов и последовательно объединяет следующую ближайшую пару классов, и следующую ближайшую пару до тех пор, пока все классы не будут объединены в один класс. После каждого объединения расстояния между всеми парами классов обновляются. Для построения древовидной схемы используются расстояния, при котором сигнатуры файлов объединяются.
Если не отмечена опция Использовать вероятность при расчете расстояния (Use variance in distance calculations) (MEAN_ONLY в Python), расстояние dmn между парой классов m и n измеряется как расстояние между их средними значениями:
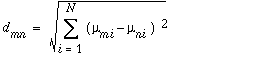
, где:
m и n – Идентификаторы классов
i – Номер слоя
µ – Среднее класса m или n в слое i
Если отмечена опция дисперсии (VARIANCE в Python), инструмент Древовидная схема (Dendrogram) измеряет расстояния между парами классов, основываясь на их средних значениях и дисперсиях с использованием следующей формулы:
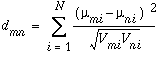
где V – это дисперсия класса m или n в слое i.
Новая статистика (средние и дисперсия), характеризующая объединенный класс, основывается на исходных значениях среднего и дисперсии эталонов, образующих объединенный класс. Следовательно, объединенный класс создается с использованием совокупных среднего и дисперсии. Две сигнатуры, которые используются для создания объединенного класса, заменяются единой сигнатурой комбинированного класса. Новая усредненная сигнатура вычисляется на основании положения в многомерном атрибутивном пространстве всех ячеек объединенного класса. Новая сигнатура в качестве идентификатора ID объединенного класса сохраняет меньшее из значений двух входных классов.
Уровни значений, или расстояния, при котором объединяется каждая пара классов, могут быть проинтерполированы с использованием делений шкал на древовидной схеме. Из-за ограничений по размеру символов (грубого расширения схемы), уровни объединения для целей отображения округляются. Однако точные значения уровней объединения представлены в виде расстояний (DISTANCE) в таблице, связанной с древовидной схемой.
После объединения классов для вычисления расстояний используются дисперсии, а не ковариации. Алгоритм, применяемый инструментом Древовидная схема (Dendrogram), не использует для определения расстояний между классами расстояние Махаланобиса. Следовательно, расстояния между классами и объединенные классы могут не совпадать с результатами тех инструментов обработки гридов, которые основаны на вычислениях расстояния Махаланобиса, например, Редактировать сигнатуры (Edit Signatures), Классификация по методу максимального подобия (Maximum Likelihood Classification) и Вероятность классов (Class Probability).
Древовидную схему можно использовать для уменьшения статистически неправильной классификации в анализе путем предоставления информации, необходимой для объединения или разделения классов данных. Если классы в анализе статистически близки (то есть, определение отличий двух классов на основе их статистических данных может оказаться трудной задачей), это может привести к неправильной классификации. В этом случае следует рассмотреть возможность слияния классов. Определенные правила определения необходимости слияние классов или отсутствия таковой необходимости отсутствуют. Когда следует выполнять слияние классов? Это зависит от гетерогенности изучаемой территории и данных, количеству классов, на которое разбиваются данные, и целей изучения. Например, если изучаемая территория является достаточно гетерогенной, имеются возможности организации множества отдельных классов, поэтому их слияние не будет являться необходимостью. Другая ситуация может характеризоваться гомогенностью данных, которые желательно классифицировать по большому количеству классов. В этом втором примере классы будут статистически очень близки, что делает допустимым слияние некоторых из них.
Если анализ не требует детализированных классов, можно объединить классы в более общие категории, чтобы снизить вероятность ошибочной классификации. В древовидной схеме показано, какие классы статистически близки, однако вам следует полагаться на собственные знания предмета и свои цели, чтобы определить, следует ли выполнять слияние классов.
Например, допустимо объединять классы «Сильно увлажненные земли» и «Торфяное болото». Однако собранные статистические данные по этим двум классам очень схожи; поэтому эти два класса будут близко располагаться друг к другу в итоговой древовидной схеме. Если вы заинтересованы только в определении заболоченной местности, имеет смысл выполнить слияние классов торфяных болот и сильно увлаженных земель.
Древовидная схема не только идентифицирует, какие классы могут быть объединены, но также показывает, есть ли преимущества от добавления классов. Если класс статистически удален от другого класса, может понадобиться добавить классы для дальнейшего уточнения классификации. Например, один класс может быть указан как урожай, другой – как трава. На итоговой древовидной схеме два класса могут располагаться далеко друг от друга. Предположим однако, что используется многоканальный растр высокого разрешения. При анализе сельскохозяйственной продукции в регионе данные высокого разрешения могут допустить включение классов урожая, и травы в определенные типы урожая.
Пример:
В следующем примере классы 3 и 5 являются ближайшими соседями в атрибутивном пространстве; следовательно, они объединяются на уровне 3.443. Это значение указывает на относительную степень сходства, которое может также рассматриваться как расстояние в многомерном пространстве. Два класса объединяются и рассматриваются как единый класс. Вычисляются статистика для объединенного класса и расстояния от объединенного класса до других классов. Затем определяются следующие два ближайших класса. Два кандидата – это классы 4 и 6. Расстояние между ними равно 3.609, и они объединяются. Затем процесс повторяется. Все классы последовательно объединяются в классы большего размера до тех пор, пока все классы не будут объединены в один единственный класс.
- Параметры, используемые в диалоговом окне инструмента Древовидная схема (Dendrogram):
Входной файл сигнатур (Input signature file) – isoclust12.gsg
Выходной файл древовидной схемы (Output dendrogram file) – isodendro.txt
Использовать вероятность при расчете расстояния (Use variance in distance calculations) – {значение по умолчанию}
Ширина линии древовидной схемы (Line width of dendrogram) – 78
В результате выходной файл древовидной схемы будет выглядеть следующим образом:
Distances between pairs of combined classes (in the sequence of merging):
Remaining Merged Between-Class
Class Class Distance
----------------------------------
3 5 3.442680
4 6 3.608904
7 9 3.899360
2 7 3.795288
3 4 4.883098
2 8 6.073256
1 3 6.257798
1 2 9.350019
----------------------------------
Dendrogram of /discb/topdir/myspace/isoclust12.gsg
C DISTANCE
L
A
S 0 1.0 2.1 3.1 4.1 5.2 6.2 7.2 8.3 9.3
S |-------|-------|-------|-------|-------|-------|-------|-------|------
5 -------------------------|
|----------|
3 -------------------------| |
|----------|
6 ---------------------------| | |
|--------| |-------------------|
4 ---------------------------| | |
| |
1 -----------------------------------------------| |
|-
9 -----------------------------| |
| |
7 ---------------------------------------------| |
| | |
2 ------------------------------| |---------------------|
|
8 ---------------------------------------------|
|-------|-------|-------|-------|-------|-------|-------|-------|------
0 1.0 2.1 3.1 4.1 5.2 6.2 7.2 8.3 9.3