Доступно с лицензией Spatial Analyst.
Инструмент Нечеткое наложение (Fuzzy Overlay) позволяет анализировать возможность явления принадлежать нескольким наборам в анализе наложения с несколькими критериями. Инструмент Нечеткое наложение (Fuzzy Overlay) не только определяет, к какому набору может относится явление, он также анализирует отношения между принадлежностями к нескольким наборам.
Тип наложения (Overlay type) предоставляет список методов, доступных для комбинирования данных на основе анализа теории множеств. Каждый метод позволяет изучать принадлежность каждой ячейки, принадлежащей к различным входным критериям. Доступные методы: Нечеткий И (Fuzzy And), Нечеткий Или (Fuzzy Or), Нечеткое произведение (Fuzzy Product), Нечеткая сумма (Fuzzy Sum) и Нечеткая гамма (Fuzzy Gamma). Каждый подход обеспечивает различные аспекты принадлежности каждой ячейки нескольким входным критериям.
Нечеткое И (Fuzzy And)
Тип наложения нечеткий И (fuzzy And) выдаст минимальное значение наборов, которым принадлежит ячейка. Этот метод полезен, если вы хотите определить наименьший общий знаменатель для принадлежности всех входных критериев. Например, в модели пригодности жилья вы можете выбрать только ячейки, которые имеют по крайней мере 0,5 или более возможность быть подходящими для всех критериев.
Нечеткое И (Fuzzy And) использует следующую функцию в рельефе:
fuzzyAndValue = min(arg1, ..., argn)Нечеткое ИЛИ (Fuzzy Or)
Тип наложения Нечеткий ИЛИ (fuzzy Or) выдаст максимальное значение наборов, которым принадлежит ячейка. Этот метод полезен, если вы хотите определить наибольшее значение принадлежности для всех входных критериев. Например, в модели пригодности жилья вы можете выбрать все ячейки, у которых по крайней мере один критерий полностью находится в подходящем наборе, значение 1.
Нечеткое ИЛИ (Fuzzy Or) использует следующую функцию в рельефе:
fuzzyOrValue = max(arg1, ..., argn)Нечеткое произведение (Fuzzy Product)
Тип наложения нечеткое произведение (fuzzy Product) для каждой ячейки умножит нечеткое значение для всех входных критериев. Полученный продукт будет меньше, чем любые из входных данных, и если член многих наборов – входные данные, значение может быть очень маленьким. Трудно коррелировать продукт всех входных критериев в относительное отношение значений. Опция нечеткое произведение (fuzzy Product) используется нечасто.
Нечеткое произведение (Fuzzy Product) использует следующую функцию в рельефе:
fuzzyProductValue = product(arg1, ..., argn)Нечеткая сумма (Fuzzy Sum)
Тип наложения нечеткая сумма (fuzzy Sum) добавит нечеткие значения каждого набора, к которому принадлежит ячейка. Результирующая сумма – это увеличивающаяся функция линейных комбинаций, которая основана на ряде критериев, введенных в анализ.
Нечеткая сумма (Fuzzy Sum) – это не алгебраическая сумма, и ее не следует путать с аддитивным подходом, используемым в инструментах Взвешенное наложение (Weighted Overlay) и Взвешенная сумма (Weighted Sum). При этих двух подходах наложения предполагается, что чем более благоприятные входные данные, тем лучше. Добавить все значения принадлежности в анализе нечеткой суммы (fuzzy Sum) – не обязательно означает, что местоположение наиболее подходящее. Опция нечеткая сумма (fuzzy Sum) используется не часто.
Нечеткая сумма (Fuzzy Sum) использует следующую функцию в рельефе:
fuzzySumValue = 1 - product(1 - arg1, ..., 1 - argn)Нечеткая гамма (Fuzzy Gamma)
Тип нечеткая гамма (fuzzy Gamma) – это алгебраическое произведение нечеткого произведения (fuzzy Product) и нечеткой суммы (fuzzy Sum), возведенных в степень гамма. Функция генерализации:
µ(x) = (FuzzySum)γ * (FuzzyProduct)1-γЭто определенная функция, используемая в алгоритме нечеткая гамма (fuzzy Gamma):
fuzzyGammaValue = pow(1 - ((1 - arg1) * (1 - arg2) * ...), Gamma) *
pow(arg1 * arg2 * ..., 1 - Gamma)Если задано значение гамма 1, выходные данные сходны с нечетной суммой (fuzzy Sum); если гамма – 0, выходные данные сходны с нечетким произведением (fuzzy Product). Промежуточные значения позволят вам комбинировать данные между двумя экстремумами (нечеткий ИЛИ и нечеткий И). Нечеткая гамма (fuzzy Gamma) – компромисс между эффектами увеличения нечеткой суммы и уменьшения нечеткого произведения. На следующем рисунке определяется отношение гамма к терминам нечеткой суммы и нечеткого произведения:
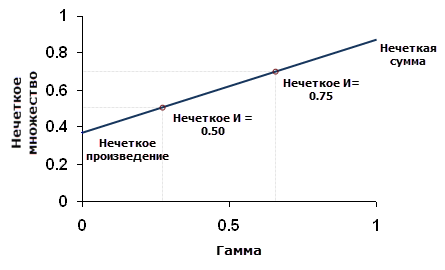
Нечеткая гамма (Fuzzy Gamma) устанавливает отношения между несколькими входными критериями и не выдает значение одного набора принадлежности, в отличие от нечеткого ИЛИ (fuzzy Or) и нечеткого И (fuzzy And).
Вы можете использовать алгоритм нечеткая гамма (fuzzy Gamma), если вам нужны значения, большие, чем нечеткое произведение (fuzzy Product), но меньшие, чем нечеткая сумма (fuzzy Sum).