Как работает Пересчет по функции

Доступно с лицензией Spatial Analyst.

Инструмент Пересчет по функции позволяет вам использовать математическую функцию (линии или кривой), чтобы назначить значения пригодности входному растру по непрерывной шкале (обычно от 1 до 10). Пересчет по функции обычно используется при моделировании пригодности. Зачастую пригодность меняется непрерывно с изменением значений критерия и практически всегда это происходит нелинейным образом. Например, местоположения ячеек, близкой к существующим дорогам, может быть наиболее предпочтительным в модели пригодности жилья, так как затраты на получение энергии в этих местоположениях меньше. По мере увеличения расстояния от дороги, затраты на получение энергии этих местах могут увеличиться в геометрической прогрессии. В результате, пригодность для более удалённых местоположений может уменьшаться драматически. Как только стоимостное взаимодействие установлено, экспоненциальное снижение предпочтений преобразуется к указанной непрерывной шкале пригодности, например, от 1 до 10. Масштабированный стоимостной критерий может быть интегрирован с другими критериями масштабирования, такими как уклон, экспозиция и расстояние от школ, для выявления наилучших местоположений для домов.

Четыре главных соображения по применению этого инструмента:

1. Понять и определить взаимодействие предпочтений между явлением и критерием.
2. Выберите функцию преобразования, которая лучше отражает взаимодействие предпочтений (например, Экспоненциальный рост).
3. Дополнительно, измените параметры функции для получения лучшего варианта.
4. Определите шкалу пригодности (оценки) для преобразования значений функции предпочтения (например, от 1 до 10).

Инструмент Пересчет по функции расширяет ваши возможности преобразования данных в модели пригодности. Вы можете использовать инструмент Переклассификация для переклассификации данных по категориям и инструмент Пересчет по функции для изменения шкалы (переклассификации) непрерывных данных без создания дискретных категорий. Инструмент Пересчёт по функции обеспечивает разнообразие функций для модели пригодности, которые изменяются по непрерывной шкале. Поскольку инструмент пересчитывает входные значения растра по непрерывной шкале пригодности, то отсутствует агрегация значений в категории, что позволяет вам лучше охватить определенные непрерывно меняющиеся взаимосвязи предпочтений (для приведенного выше примера, стоимость изменяется по мере увеличения расстояния от дороги).

Доступные функции: Exponential, Gaussian, Large, Linear, Logarithm, Logistic Decay, Logistic Growth, MSLarge, MSSmall, Near, Power, Small и Symmetric Linear. Более подробные сведения для каждой из отдельных функций доступны здесь:

• Функции преобразования, доступные для Пересчета по функции

Вы можете определить верхний и нижний пороги, чтобы взять больший контроль над тем, как изменяется масштаб входных значений. Для более подробной информации см. Взаимодействие нижнего и верхнего порогов для выходных значений.

Основные термины

Следующие определения используются для некоторых, часто используемых терминов при обсуждении Пересчет по функции.

• Явление – Моделируемый элемент (например, олень, дом, дорога или торговый центр).
• Значение предпочтения – Значение, указывающее на то, насколько явление предпочитает объект в конкретном местоположении.
• Критерий – Объект, которому соответствует явление (например, уклон, экспозиция, расстояние от дороги или тип землепользования).
• Значение пригодности – Тоже, что и значение предпочтения, за исключением предпочтения в контексте модели пригодности.
• Оценочная шкала – Относительная шкала для размещения значений предпочтений или пригодности. Как правило, ячейка, приписанная к наивысшему оценочному значению, содержит объекты, которые являются более предпочтительными для явления по отношению к анализируемому критерию. Общие оценочные шкалы включают: от 1 до 10, от 0 до 1 и от 1 до 100.
• Шкала пригодности – Тоже, что и оценочная шкала.
• Непрерывные значения – Значения в растре имеют относительное значение. Например, ячейка 100 метров над уровнем моря наполовину ниже ячейки со значением 200 метров. Примеры непрерывных данных включают высоту, концентрации озона и значения пригодности.
• Категорийные значения – Значения в растре не имеют относительного значения. Например, ячейка с типом землепользования 4 не является половиной использования земли ячейки с типом 8. Примеры категорийных данных включают типы землепользования, названия округов и почтовые индексы.
• Непрерывная выходная шкала – Значения в пределах указанного диапазона непрерывно увеличиваются или уменьшаются без дискретных классов. Обычно, непрерывные значения представлены значениями с плавающей точкой.

Преобразование данных

Инструмент Пересчёт по функции пересчитывает непрерывные данные по заданной шкале пригодности, на основе математической функции (такой как Экспоненциальная, Степень и Логарифмическая), которую можно выбрать. Преобразование входных данных, концептуально, представляет собой двух-шаговый процесс, вначале применяется функция преобразования, а затем значения функции распределяются по шкале пригодности (обычно от 1 до 10).

Применение функции преобразования.

Заданная функция применяется к значениям, которые попадают между значениями нижнего и верхнего порогов.

Пересчет преобразованных данных по оценочной шкале

Следующий график иллюстрирует как значения функции распределяются по оценочной шкале.

Пример преобразования значений функции для функции Степень по оценочной шкале

Минимальные и максимальные преобразованные значения функции f(x) пересчитываются к минимуму и максимуму оценочной шкалы, соответственно. Многие из функций являются монотонными (непрерывно возрастающими или убывающими). В результате, нижний и верхний пороги обычно отображаются в минимальные и максимальные значения на оценочной шкале, так как они будут наиболее низким и наиболее высоким значениями f(x).

В предыдущем примере, нижний и верхний пороги эквивалентны минимуму и максимуму входных данных (3000 и 5000, соответственно). В результате, самому низкому входному значению присваивается значение 1 по оценочной шкале от 1 до 10, а максимальному входному значению – 10. Но это не должно происходить обязательно. Например, если функция Степень применяется к тем же входным данным (от 3000 до 5000), и, если нижний порог задан как 3500 и верхний порог как 4500, то ячейке со входным значением 3500 будет присвоено значение 1 по оценочной шкале от 1 до 10, и ячейке со входным значением 4500 будет присвоено 10. Все остальные значения будут варьироваться между этими двумя, основываясь на их преобразованном значении. Входным значениям ниже нижнего порога и выше верхнего порога будут присвоены указанные вами значения.

Пример преобразования значений функции для Гауссовой функции по оценочной шкале

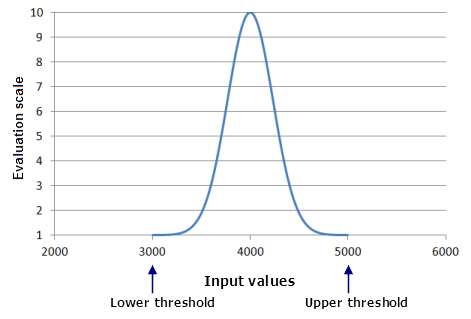
Не все функции непрерывно увеличиваются или уменьшаются, поэтому самые низкие и самые высокие входные значения не всегда сопоставляются с самыми низкими и самыми высокими оценочными значениями. По умолчанию, в Гауссовой функции, серединой является значение, которое определяет самую высокую точку функции (наиболее предпочтительное значение). Этим устанавливается середина ваших входных данных. Местоположения с минимальными и максимальными входными значениями, будут производить самые низкие значения функции f(x), как только Гауссова функции будет применена. Таким образом, ячейкам с минимальными и максимальными входными значениями будет присвоено значение 1 в выходном растре. Значение середины производит самые высокие значения функции f(x). В результате, ячейкам, содержащим входные значения равные этой середине, будет присвоено значение 10 в выходном растре.

Гауссова функция может быть полезна в модели пригодности для выявления лучшей среды обитания для редких видов орхидей Masdevallia. Орхидеи чувствительны к высоте. Лучше всего они растут на высоте около 4000 метров. Поскольку высота увеличивается с этой позиции, то для орхидей быстро становится слишком холодно; с уменьшением высоты становится слишком тепло. При перерасчете высоты, значение 4000 метров является наиболее предпочтительным, а другие высоты (как выше, так и ниже) являются наименее предпочтительными.

Вы можете назначить любое входное значение ниже нижнего порога или выше верхнего порога требуемому выходному значения (в пределах или за пределами оценочной шкалы, или значение NoData) с помощью параметров Значение ниже порога и Значение выше порога. Функция преобразования не будет применена к данным местоположениям.

Определение преобразования

Существуют два основных подхода при определении непрерывного преобразования:

• Принятие параметров по умолчанию.

  Форморегулирующие параметры (см. описание ниже) будут рассчитаны так, чтобы вписать функцию между минимальным и максимальным значениями входного растра. Это зависимый от данных сценарий, так как функция подгоняется к данным.

• Выберите функцию, которая лучше моделирует пригодность.

  Измените форморегулирующие параметры функции для тонкой настройки формы функции на лучшее отражение пригодности. Чтобы сделать функцию независимой от данных, установите нижний и верхний пороги для соответствующих значений с целью подгонки предпочтения явления к критерию значений, независимо от значений входных данных.

Параметры функции преобразования

Типы параметров функции

Существуют два типа параметров, связанных с каждой функцией преобразования, которые контролируют:

1. Форма функции

   Примерами параметров являются Базовый коэффициент, Сдвиг входных данных и Середина. Эти параметры определяют, насколько круто увеличивается или уменьшается функция, где начинается оценка функции и где расположены точки перехода функции.

2. Отображение функции на оценочной шкале пригодности

   Примерами этого являются пороговые параметры, такие как Нижний порог и Значение выше порога.

Общий формат параметров функции

Ниже приведен общий формат параметров для каждой функции и их характеристики:

• Функция ({Параметр формы 1}, {{Параметр формы 2}, {{Параметр формы 3}, {Нижний порог}, {Значение ниже порога}, {Верхний порог}, {Значение выше порога})

Для этих параметров

1. Каждая функция состоит из форморегулирующих параметров и соответствующих пороговых параметров.
2. Число форморегулирующих параметров зависит от функции преобразования; большинство функций имеет два параметра, а некоторые функции имеют три.
3. Пороговые параметры действуют для всех функций.
4. Значения по умолчанию для форморегулирующих параметров вычисляются с использованием значений данных из входного растра.
5. Все параметры для функции являются дополнительными.
6. Значением параметров Значение ниже порога и Значение выше порога может быть число (с двойной точностью) или строка "NoData". Все остальные параметры имеют тип числа с двойной точностью (double).

Пример общего формата Экспоненциальной функции

Чтобы продемонстрировать, как общий формат, описанный выше, следует применять к определенной функции преобразования, приводится следующий вариант, в котором Функция преобразования была установлена как Экспоненциальная:

• Экспоненциальная (Сдвиг входных данных, Базовый коэффициент, Нижний порог, Значение ниже порога, Верхний порог, Значение выше порога)

Сдвиг входных данных и Базовый коэффициент являются форморегулирующими параметрами. Нижний порог, Значение ниже порога, Верхний порог и Значение выше порога являются пороговыми параметрами.

По умолчанию, минимальное и максимальное значения данных определяют нижнюю и верхнюю границы для функции.

Взаимодействие параметров в диалоговом окне инструмента

Для параметра Входной растр, Нижний порог установлен на минимальное значение в растре, Верхний порог установлен на максимальное значение в растре, а форморегулирующие параметры (например, Сдвиг входных данных, Базовый коэффициент и Середина) рассчитываются автоматически для наилучшей подгонки (сдерживания) функции между Нижним порогом и Верхним порогом.

Существует взаимодействие между пороговыми параметрами, которые управляют отображением значений функции на шкале пригодности, и форморегулирующими параметрами, которые определяют кривую функции. Например, как только значения по умолчанию определены, вы можете ввести большее значение для Верхнего порога. Соответствующие форморегулирующие параметры будут пересчитаны и обновлены в диалоговом окне (например, Сдвиг входных данных и Базовый коэффициент). Тем не менее, если вы введете новое значение для одного из форморегулирующих параметров (например, новый Базовый коэффициент), то связь с соответствующими пороговыми параметрами, контролирующими отображение на шкале пригодности будет разорвана и вы будете затем в управлении. Рассмотрим в качестве примера Экспоненциальную функцию, если вы введете новый Базовый коэффициент и измените Верхний порог, новый Базовый коэффициент не будет автоматически вычисляться. Инструмент будет использовать заданный вами Базовый коэффициент. В качестве другого примера используем Линейную функцию, по умолчанию Верхний порог установлен на максимум Входного растра. Если ввести большее значение для Верхнего порога, то параметр Максимум для Линейной функции будет автоматически обновлен. Тем не менее, если вы введете новое значение Максимума и измените Верхний порог, то Максимум не изменится.

С помощью этого диалогового взаимодействия, функция по умолчанию вписывается между Нижним порогом и Верхним порогом, которые изначально настроены на минимум и максимум Входного растра. Тем не менее, вы можете иметь полный контроль над формой функции и её отображением на оценочной шкале посредством ввода ваших собственных значений.

Если вы изменяете параметр функции и хотите вернуть его к значению по умолчанию, то вы можете выбрать и удалить значение, затем щёлкнуть в поле другого параметра, что заставит пустой параметр вернуться к значению по умолчанию. Например, если вы ввели значение для Базового коэффициента, но хотите вернуться для того, чтобы подогнать функцию между Нижним порогом и Верхним порогом, то удалите значение параметра Базовый коэффициент, щелкните в поле другого параметра, и новый Базовый коэффициент будет вычислен для подгонки функции между порогами.

Примечание:

Функции MSSmall и MSLarge не следуют этому поведению взаимодействия, потому что две эти функции зависят от среднего и стандартного отклонения входного набора данных.