Как работает инструмент Статистика набора каналов

Доступно с лицензией Spatial Analyst.

Инструмент Статистика набора каналов предоставляет статистику для многомерного анализа набора каналов растра. При использовании опции Вычислить ковариационную и корреляционную матрицу, помимо основных статистических параметров, таких, как минимум, максимум, среднее и стандартное отклонение для каждого слоя, в качестве выходных данных будут также получены матрицы ковариации и корреляции.

Матрица ковариации содержит значения дисперсий и ковариаций. Дисперсия – это статистическая мера, показывающая величину отклонений от среднего. Для вычисления дисперсии находится среднее из квадратов разницы между значением ячейки и средним значением для всех ячеек. Дисперсии для каждого слоя могут быть прочитаны по диагонали матрицы ковариации, которая проходит из верхнего левого угла в правый нижний угол матрицы. Дисперсии выражаются как квадрат единиц измерения значений ячеек.

Остальные значения в матрице ковариации – это ковариации между всеми парами входных растров. Для определения ковариации между слоями i и j применяется следующая формула:

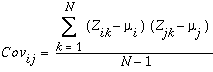
• , где:

  Z – значение ячейки

  i, j – слои стека

  µ – среднее значение слоя

  N – число ячеек

  k – обозначает конкретную ячейку

Ковариация двух слоев – это пересечение соответствующей строки и столбца. Ковариация между слоями 2 и 3 – это то же самое, что и ковариация между слоями 3 и 2. Значения матрицы ковариации зависят от единиц измерения значений, в то время как значения матрицы корреляции не зависят от единиц измерения значений.

Матрица корреляции показывает значения коэффициентов корреляции, которые указывают на связь между двумя наборами данных. В случае набора слоев растра, матрица корреляции отражает связь значений ячеек с одного слоя растра со значениями ячеек на другом слое растра. Корреляция между двумя слоями – это мера зависимости между слоями. Это ковариация между двумя слоями, деленная на произведение их стандартных отклонений. Поскольку это отношение, его значение является безразмерным. Уравнение для вычисления корреляции следующее:

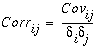
Коэффициенты корреляции находятся в диапазоне от +1 до -1. Положительная корреляция указывает на прямую связь между двумя слоями, то есть когда значения ячеек на одном слое увеличиваются, скорее всего, будут увеличиваться и значения ячеек на другом слое. Отрицательная корреляция означает, что переменная меняется по отношению к другой переменной противоположным образом. Нулевой коэффициент корреляции означает, что два слоя независимы друг от друга.

Матрица корреляции симметрична. Ее значения по диагонали из верхнего левого угла в нижний правый угол равны 1.0000, поскольку коэффициент корреляции для идентичных слоев равен +1.

Пример:

Пример, приведенный ниже, иллюстрирует содержание выходных данных инструмента Статистика набора каналов для многоканального растра, состоящего из четырех слоев. В первой таблице приведены основные статистические показатели для случая, когда опция Вычислить матрицы не используется. Однако в тех случаях, когда эта опция отмечена, вычисляются также матрицы ковариации и корреляции. В примере приведена выходная статистика, содержащаяся в выходном файле статистики.

Только среднее значение вычисленное

Выходные данные с отключенной опцией Вычислить ковариационную и корреляционную матрицу (BRIEF):

#               STATISTICS of INDIVIDUAL LAYERS
#   Layer           MIN          MAX          MEAN         STD
# ---------------------------------------------------------------
       1            1.0000      21.0000       7.8410       4.1690
       2            1.0000     128.0000      25.5144      35.8494
       3          296.9573    4073.6306    1565.5359     763.9803
       4            0.3333     127.5000      51.5314      29.7958
# ===============================================================

Вычисляются среднее значение и матрицы

Выходные данные с включенной опцией Вычислить ковариационную и корреляционную матрицу (DETAILED):

#               STATISTICS of INDIVIDUAL LAYERS
#   Layer           MIN          MAX          MEAN         STD
# ---------------------------------------------------------------
       1            1.0000      21.0000       7.8410       4.1690
       2            1.0000     128.0000      25.5144      35.8494
       3          296.9573    4073.6306    1565.5359     763.9803
       4            0.3333     127.5000      51.5314      29.7958
# ===============================================================
#                    COVARIANCE MATRIX
#   Layer            1            2            3            4
# ---------------------------------------------------------------
       1           17.3826      16.9320    3177.5947      87.9590
       2           16.9320    1285.3096    3117.1753      31.3420
       3         3177.5947    3117.1753  583723.0625   16137.9785
       4           87.9590      31.3420   16137.9785     887.8751
# ===============================================================
#                    CORRELATION MATRIX
#    Layer            1            2            3            4
# ---------------------------------------------------------------
       1            1.0000       0.1133       0.9976       0.7080
       2            0.1133       1.0000       0.1138       0.0293
       3            0.9976       0.1138       1.0000       0.7089
       4            0.7080       0.0293       0.7089       1.0000
# ===============================================================

Литература

Snedecor, G. W., and W. G. Cochran. 1968. Statistical Methods, 6th ed. Ames, Iowa: The Iowa State University Press.