Как работают инструменты стоимостного расстояния

Доступно с лицензией Spatial Analyst.

Тогда как эвклидово расстояние является прямой линией (расстоянием между местоположениями), Стоимостное расстояние учитывает перемещение по рельефу. Инструменты стоимостного расстояния обычно используются для создания оптимального пути или коридора между источником и назначением.

Примеры проблем, решаемых анализом стоимостного расстояния

• Определение наиболее дешевого маршрута для постройки дороги к новой школе.
• Соединение наилучших мест обитания рыси естественными коридорами, что позволит рыси свободно перемещаться между ними.
• Размещение нового трубопровода для соединения нефтяного месторождения с перерабатывающим заводом.
• Определение наиболее быстрого пути к пострадавшему альпинисту в удаленном районе.
• Передвижение военной техники к месту выполнения задачи по пересеченной местности.

Общая формула анализа стоимости

На стоимость перемещения из одной ячейки в другую влияет следующее:

1. Характеристики поверхности (стоимость поверхности)
2. Характеристики перемещающегося объекта. Сюда же относится режим передвижения, пешком или с помощью транспортных средств.
3. Характеристики перемещения из одной ячейки в другую, например, движение вверх или вниз по склону.

Общая формула стоимостного расстояния имеет следующий вид:

Cost = Cost of travel  *  Characteristics  *  Movement characteristics       over surface       of the mover        on the surface

Инструменты стоимостного расстояния получают характеристики поверхности через поверхность стоимости, как описывается ниже. Чтобы узнать, как управлять характеристиками перемещающегося объекта в инструментах расстояния, обратитесь к разделу Как характеристики источника влияют на анализ стоимостного расстояния. Инструмент Путевое расстояние позволяет задать характеристики перемещения из ячейки в ячейку с помощью растра поверхности и горизонтальных и вертикальных коэффициентов.

Стоимостное расстояние и Стоимостная связанность

Инструмент Стоимостная связанность создан для создания сети оптимальных путей между сериями входных регионов. Последовательность инструментов Стоимостное расстояние и Оптимальный путь позволяет создать пути между определенными источниками и назначениями. Однако, иногда для создания сети путей с использованием итеративного изолирования региона как источника и его соединения с другими регионами, определенными как назначения, используются две последовательности инструментов. Этот процесс повторяется для каждого региона и полученные пути наименьшей стоимости объединяются.

У итеративного подхода имеются следующие ограничения.

• Соединение всех регионов между собой может привести к появлению слишком большого числа путей, особенно при большом количестве регионов. Также, в полученной сети игнорируется постепенный подход при определении связности; т.е., для достижения удаленного региона, можно использовать набор путей, соединяющих последовательность регионов, находящихся между вами и местом назначения.
• Чтобы уменьшить число комбинаций путей, во много раз, соединяются два ближайших региона – для определения источника и назначения используется эвклидово расстояние. Однако два региона могут быть расположены близко друг к другу, но стоимость перемещения между ними может быть высока, например, из-за гор или рек; поэтому, более эффективно соединять регионы на основе сходной стоимости, как это происходит в Стоимости связности.

  

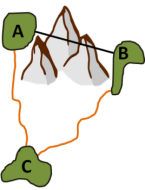
  Даже если регионы A и B являются близкими в Евклидовом расстоянии, из-за гор они очень далеки по стоимостному расстоянию.

• Часто различные пути из разных регионов соединяются и следуют по одному пути в общий регион (они частично используют один и тот же общий путь наименьшей стоимости). Трудно управлять и анализировать общую часть этих растровых путей; поэтому, при проведении последовательного анализа лучше, если каждая часть обрабатывается как отдельная от других.
• Пути, создаваемые инструментом Оптимальный путь достигают только ребра полигонального региона или местоположения линии для линейных регионов. В результате отдельные пути не соединяются, т.е. не получается сеть.

Вычисление стоимостного расстояния

Все инструменты стоимостного расстояния используют, по сути, тот же алгоритм для вычисления выходных данных. Основное различие определяется по первичным выходным данным каждого инструмента.

Инструмент Стоимостное расстояние создает выходной растр, в котором каждой ячейке присваивается суммарная стоимость до ближайшей ячейки источника. Алгоритм применяет представление ячейки по типу узел и связь, используемому в теории графов. При представлении ячейки по принципу узел и связь, центр каждой ячейки рассматривается как узел, и каждый узел может быть соединен несколькими связями со смежными узлами.

Каждой связи поставлено в соответствие сопротивление перемещению. Сопротивление определяется, исходя из стоимости, присвоенной ячейкам на каждом конце связи (стоимость берется с поверхности стоимости), и направления движения через ячейку.

Стоимость, присвоенная каждой ячейке, представляет стоимость движения через ячейку по поверхности стоимости, выраженную на единицу расстояния. Конечное значение на ячейке – это размер ячейки, умноженный на значение стоимости. Например, если растр стоимости имеет размер ячейки 30, а определенная ячейка имеет значение стоимости 10, конечная стоимость этой ячейки равна 300 единиц.

Стоимости перемещения узлов

Стоимость перемещения между двумя смежными узлами зависит от пространственной ориентации узлов. То как связаны ячейки, также воздействует на стоимость перемещения.

Стоимость смежных узлов

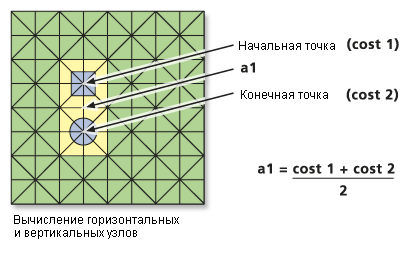
При перемещении из ячейки в одну из четырех соседних ячеек, имеющих с ячейкой общее ребро, стоимость движения по этим связям в соседний узел будет равна среднему из стоимости перемещения через ячейки 1 и 2:

 a1 = (cost1 + cost2) / 2

• Где

  cost1 – Стоимость ячейки 1

  cost2 – Стоимость ячейки 2

  a1 – Общая стоимость связи из ячейки 1 до ячейки 2

Накопление перпендикулярной стоимости

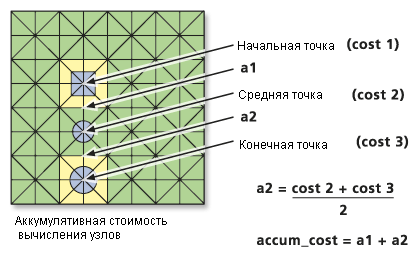
Суммарная стоимость определяется по следующей формуле:

 accum_cost = a1 + (cost2 + cost3) / 2

• Где

  cost2 – Стоимость ячейки 2

  cost3 – Стоимость ячейки 3

  a2 – Стоимость перемещения из ячейки 2 в ячейку 3

  accum_cost – Суммарная стоимость перемещения из ячейки 3 в ячейку 1

Стоимость диагонального узла

Если перемещение происходит по диагонали, стоимость перемещения по связи – 1,414214 (или квадратный корень из 2), умноженная на стоимость ячейки 1 плюс стоимость ячейки 2 и деленная на 2:

 a1 = 1.414214 (cost3 + cost2) / 2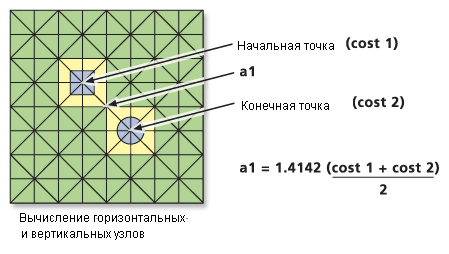

При определении совокупной стоимости для диагонального перемещения будет использована следующая формула:

 accum_cost = a1 + 1.414214(cost2 + cost3) / 2

Список ячеек с накоплением стоимости

Создание растра расстояния с суммарной стоимостью с помощью теории диаграмм может рассматриваться как попытка идентифицировать ячейку с наименьшей стоимостью и добавить ее в выходной список. Это интерактивный процесс, который начинается с исходных ячеек. Цель каждой ячейки – быть быстро присвоенной выходному растру стоимостного расстояния.

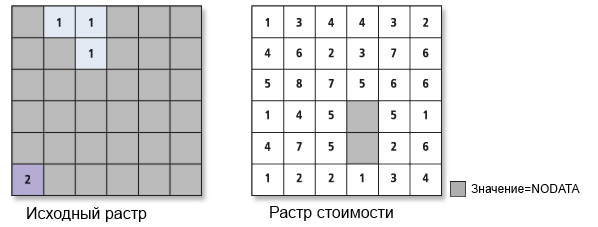
В первом повторении определяются ячейки источника, и им присваивается значение 0, т.к. нет суммарной стоимости, которую они могут вернуть себе. Далее активируются все соседи исходной ячейки, и стоимость присваивается связям между узлами исходной ячейки и узлами соседних ячеек с использованием формул суммарной стоимости выше. Каждая из этих соседних ячеек может достичь источника; следовательно, их можно выбрать или присвоить выходному растру суммарной стоимости. Чтобы быть присвоенными выходному растру, ячейки должны иметь следующий путь с наименьшей стоимостью до источника.

Значения суммарной стоимости организованы в список от наименьшей суммарной стоимости до наибольшей.

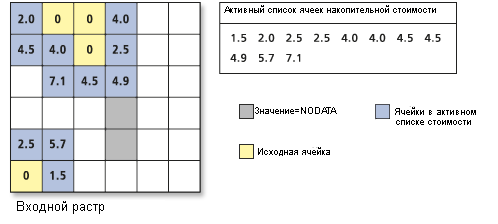
Ячейка с наименьшей стоимостью выбирается из активного списка ячеек суммарной стоимости, и значение для этой ячейки присваивается выходному растру стоимостного расстояния. Список активных ячеек расширяется, распространяясь на соседние с выбранной ячейки, т.к. у этих ячеек теперь есть способ добраться до источника. Только те ячейки, у которых есть возможность достичь источника, могут быть активными в списке. Стоимость перемещения в эти ячейки вычисляется с помощью формул суммарной стоимости.

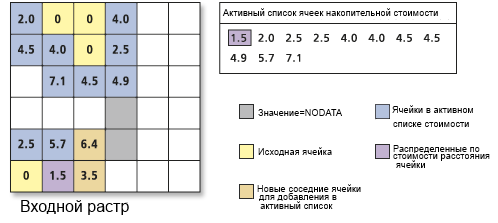
Опять же, выбирается активная ячейка в списке с наименьшей стоимостью, расширяется окрестность, вычисляются новые стоимости, и новые ячейки стоимости добавляются в активный список.

Исходные ячейки могут быть не соединены между собой. Все несвязанные источники вносят равный вклад в активный список. Выбираются и расширяются только ячейка с наименьшей суммарной стоимостью, независимо от источника, к которому она будет относиться.

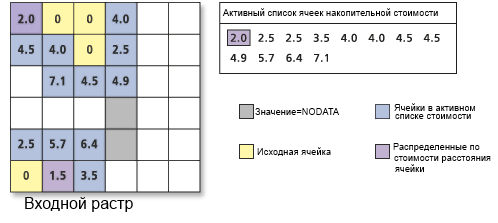
Этот процесс распределения продолжается. Кроме того, ячейки в активном списке обновляются, если создается новый, более дешевый маршрут путем добавления новых ячеек к выходному растру.

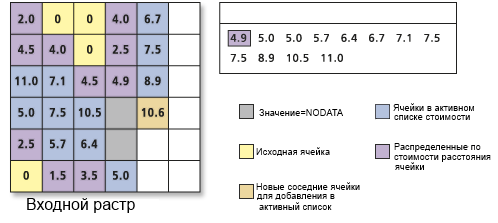
Это обновление может произойти с появлением новых путей для ячеек в активном списке, т.к. больше ячеек относятся к выходному растру. Если ячейка с наименьшим значением в активном списке суммарной стоимости относится к выходному растру, вычисляются все суммарные стоимости. Эти стоимости также вычисляются для соседних ячеек недавно присвоенной выходной ячейки, даже если соседние ячейки находятся в активном списке через другую ячейку. Если новая суммарная стоимость для ячеек в активном списке больше, чем суммарная стоимость, которую в текущий момент имеют ячейки, значение игнорируется. Если суммарная стоимость меньше, старая суммарная стоимость для ячейки заменяется в активном списке на новое значение. Эта ячейка, которая теперь имеет доступ к более дешевому и более желательному пути к источнику, перемещается вверх в активном списке.

В приведенном ниже примере ячейка в строке 3, столбце 1 (выделена), имеет суммарную стоимость 11,0, если она была помещена в активный список, чтобы достигнуть источник наверху растра. Однако, поскольку нижний источник расширен до этого местоположения, ячейки имеют доступ к пути с самой дешевой суммарной стоимостью для достижения источника. Значение для местоположения было обновлено в активном списке и распределено в выходные данные из-за этой меньшей суммарной стоимости.

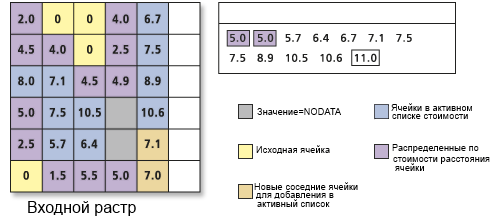
Если есть несколько зон или несвязанных наборов исходных ячеек на входном исходном растре, процесс роста продолжается и выделяет ячейку с самой дешевой стоимостью из активного списка независимо от того, из какого она источника.

Когда встречаются фронты роста, путь с наименьшей стоимостью обратно к источнику продолжается, пока все приемлемые ячейки не достигнут значения стоимости.

Можно предположить, что, когда встречаются растущие модели, ячейки из одной растущей модели сможет достичь исходную ячейку в другом наборе или растущей модели дешевле. Если это так, то они будут присвоены новому источнику. Такое поведение было ранее показано ячейкой в строке 3, столбце 1, но также приведено ниже ячейкой в строке 3, столбце 6.

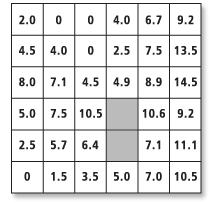
Если из активного списка были выбраны все ячейки, результатом будет растр суммарной стоимости или взвешенного расстояния. Используемая процедура гарантирует, что минимальная накопительная стоимость гарантируется для каждой ячейки. Этот процесс продолжается для всех ячеек, пока не встретится ребро растра, не будет достигнута граница окна или не будет достигнуто минимальное расстояние.

Не допускается перемещение через ячейки, содержащие значения NoData. Минимальная суммарная стоимость для ячеек на обратной стороне группы ячеек со значением NoData определяется по стоимости перемещения вокруг этих ячеек. Если ячейке присваивается значение NoData на выходном растре стоимости, значение NoData будет присвоено ячейке на выходном растре стоимостного расстояния.

Выходные значения стоимостного расстояния