Как работает инструмент Отмывка

Доступно с лицензией Spatial Analyst.

Доступно с лицензией 3D Analyst.

Инструмент Отмывка позволяет получить гипотетическое освещение поверхности путем определения освещенности для каждой ячейки растра. Принцип его работы заключается в установке положения гипотетического источника света и вычислении значений освещенности каждой ячейки по отношению к соседним ячейкам. Применение функции может значительно улучшить визуальное представление поверхности для анализа и графического отображения, особенно, при использовании опции прозрачности.

По умолчанию, тень и свет – это оттенки серого, связанные с целыми числами от 0 до 255 (возрастающие от черного к белому).

Параметры отмывки

Главным фактором при создании карты отмывки для конкретного местоположения является расположение солнца на небе.

Азимут

Азимут – это угловое направление на солнце, измеренное по часовой стрелке с севера в градусах от 0 до 360. Азимут 90 градусов – направление на восток. Азимут по умолчанию – 315 градусов (NW).

Азимут (направление) солнца по умолчанию для отмывки – 315 градусов.

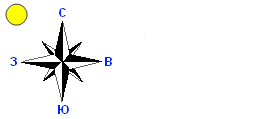
Высота

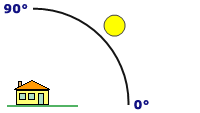
Высота - это подъем или угол источника света над горизонтом. Единицы – в градусах, от 0 (на горизонте) до 90 (над головой). Значение по умолчанию равно 45 градусам.

Высота солнца по умолчанию для отмывки – 45 градусов.

Пример Отмывки

В примере отмывки ниже азимут равен 315 градусам, а высота – 45 градусам.

Пример выходных данных инструмента Отмывка

Использование отмывки для отображения

Помещая растр высот поверх растра отмывки и настраивая его прозрачность вы можете создать визуально привлекательную карту рельефа ландшафта. Подробнее о том, как настроить отображение и оформление, см Оформление изображения.

Использование прозрачности для объединения растра высот с отмывкой.

Вы можете добавить другие слои, например, типов землепользования, растительности, дорог или водотоков, для увеличения информационного содержания в отображении.

Использование отмывки в анализе

Моделируя тень (опция по умолчанию), вы можете вычислить локальное освещение и то, попадают ли ячейки в тень или нет.

Моделируя тень, вы можете определить каждую ячейку, которая будет в тени другой ячейки в определенное время дня. Ячейкам в тени другой ячейки дается код 0; всем другим ячейкам дается код целого числа от 1 до 255. Вы можете переклассифицировать все значения, которые больше 1, в 1, создавая бинарный выходной растр. В примере ниже черные области – в тени. Азимут одинаковый на каждом изображении, но высота солнца была изменена.

Большая площадь затенения при небольшой высоте солнца

Небольшое затенение при большой высоте солнца

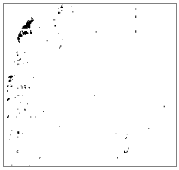
Вычисление отмывки рельефа

Чтобы вычислить значение тени, сначала необходимо получить высоту и азимут положения источника света. Эти значения будут обрабатываться вместе с вычислениями уклонов и экспозиции для определения окончательного значения отмывки для каждой ячейки на выходном растре.

Алгоритм отмывки

Применяется следующий алгоритм вычисления значения отмывки:

(1) Hillshade = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad)))

Обратите внимание, что если вычисленное значение отмывки меньше 0, выходное значение ячейки будет равно 0.

Вычисление угла положения источника света

Высота источника света задается в градусах над горизонтом. Однако для формулы вычисления значения отмывки необходимо, чтобы угол был выражен в радианах и было известно отклонение от вертикали. Направление непосредственно вверх от поверхности (прямо над головой) обозначается как 'Зенит'. Угол зенита измеряется от точки зенита до направления на источник света и в сумме с углом высоты образует 90 градусов. Чтобы вычислить угол положения источника света, сначала шага необходимо преобразовать угол высоты в угол зенита. Затем необходимо преобразовать угол в радианы.

Заменить угол высоты на угол зенита:

(2) Zenith_deg = 90.0 - Altitude

Преобразуйте градусы в радианы:

(3) Zenith_rad = Zenith_deg * pi / 180.0

Вычислить направление положения источника света

Направление положения источника света или азимут, задается в градусах. Формула вычисления отмывки предполагает, что угол выражен в радианах. Сначала угол азимута меняется с географических единиц измерения (компасного направления) на математические единицы (правильный угол). Затем необходимо преобразовать значение азимута в радианы.

Измените измерение угла азимута:

(4) Azimuth_math = 360.0 - Azimuth + 90.0

Обратите внимание, что если Azimuth_math >= 360,0, то нижеследующее выражение истинно:

(5) Azimuth_math = Azimuth_math - 360.0

Преобразовать градусы в радианы:

(6) Azimuth_rad = Azimuth_math * pi / 180.0

Вычислить уклон и экспозицию

Движущееся окно размером 3 x 3 ячейки проходит через каждую ячейку входного растра и для каждой ячейки в центре окна с использованием алгоритма, который учитывает значения восьми соседних ячеек, вычисляются значения уклонов и экспозиции. Ячейки обозначаются буквами от 'a' до 'i, при этом буква 'e' представляет ячейку, для которой вычисляется значение экспозиции.

Степень изменения по направлению x для ячейки 'e' вычисляется с помощью следующего алгоритма:

(7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize)

Степень изменения по направлению y для ячейки 'e' вычисляется с помощью следующего алгоритма:

(8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize)

Уклон – это самый крутой спуск из каждой ячейки на поверхности. Алгоритм вычисления уклона в радианах, учитывающий коэффициент по z, следующий:

(9) Slope_rad = ATAN (z_factor * √ ([dz/dx]2 + [dz/dy]2))

Экспозиция – это направление самого крутого спуска по поверхности. Экспозиция в радианах определяется в диапазоне от 0 до 2pi, при этом значение 0 соответствует направлению на восток. Экспозиция определяется по правилам следующего алгоритма:

(10) If [dz/dx] is non-zero: Aspect_rad = atan2 ([dz/dy], -[dz/dx]) if Aspect_rad < 0 then Aspect_rad = 2 * pi + Aspect_rad If [dz/dx] is zero: if [dz/dy] > 0 then Aspect_rad = pi / 2 else if [dz/dy] < 0 then Aspect_rad = 2 * pi - pi / 2 else Aspect_rad = Aspect_rad

Пример вычисления отмывки рельефа

В этом примере будет вычислено значение отмывки для центральной ячейки движущегося окна.

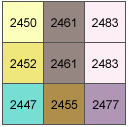
Размер ячейки равен 5 единицам измерения. По умолчанию используются значения Высоты, равной 45 градусам и Азимута, равного 315 градусам.

• Угол положения источника света

  Угол Зенита будет вычислен с использованием уравнения 2:

  (2) Zenith_deg = 90.0 - Altitude = 90.0 - 45.0 = 45.0

  И преобразован из градусов в радианы с использованием уравнения 3:

  (3) Zenith_rad = Zenith_deg * pi / 180.0 = 45.0 * 3.1415926536 / 180.0 = 0.7853981634

• Направление света

  Угол азимута будет преобразован из географического в математический с помощью уравнения 4:

  (4) Azimuth_math = 360.0 - Azimuth + 90.0 = 360.0 - 315.0 + 90.0 = 135.0

  Преобразование угла азимута в радианы выполняется с использованием уравнения 6:

  (6) Azimuth_rad = Azimuth_math * pi / 180.0 = 135.0 * 3.1415926536 / 180 = 2.3561944902

• Уклон и экспозиция

  Степень изменения в направлении x для центральной ячейки e выполняется следующим образом:

  (7) [dz/dx] = ((c + 2f + i) - (a + 2d + g)) / (8 * cellsize) = ((2483 + 4966 + 2477) - (2450 + 4904 + 2447)) / (8 * 5) = (9926 - 9801) / 40 = 3.125

  Степень изменения в направлении x для центральной ячейки e выполняется следующим образом:

  (8) [dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 * cellsize) = (2447 + 4910 + 2477) - (2450 + 4922 + 2483) / (8 * 5) = (9834 - 9855) / 40 = -0.525

  Вычисление угла уклона:

  (9) Slope_rad = ATAN ( z_factor * √ ([dz/dx]2 + [dz/dy]2)) = atan(1 * sqrt((3.125 * 3.125) + (-0.525 * -0.525))) = atan(1 * sqrt(10.04125 + 0.275625)) = atan(1 * 3.1687931457) = 1.2651101670

  Вычисление угла экспозиции в радианах Aspect_rad в соответствии с правилом 10 выполняется следующим образом: (т. к. dz/dx в этом примере не равно 0):

  Aspect_rad = atan2 ([dz/dy], -[dz/dx]) = atan2(-0.525, -3.125) = -2.9751469600

  Поскольку это значение меньше 0, эта часть правила применяется следующим образом:

  Aspect_rad = 2 * pi + Aspect_rad = 2 * 3.1415926536 + -2.9751469600 = 3.3080383471

• Отмывка

  Окончательное вычисление отмывки выполняется следующим образом:

  Hillshade = 255.0 * ((cos(Zenith_rad) * cos(Slope_rad)) + (sin(Zenith_rad) * sin(Slope_rad) * cos(Azimuth_rad - Aspect_rad))) = 255.0 * ((cos(0.7857142857) * cos(1.26511)) + (sin(0.7857142857) * sin(1.26511) * cos(2.3571428571 - 3.310567))) = 153.82

Поскольку выходной растр имеет целочисленный тип, значение затенения для центральной ячейки e = 154.

Справочная информация

Burrough, P. A., and R. A. McDonell. 1998 год Principles of Geographical Information Systems. New York: Oxford University Press.