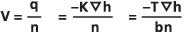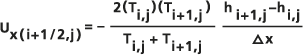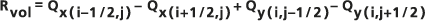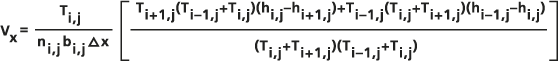Доступно с лицензией Spatial Analyst.
Инструменты Сток по Дарси и Скорость по Дарси, в совокупности с инструментами Трек частиц и Фильтрация в водоносном горизонте, могут быть использованы для выполнения элементарного адвективно-дисперсионного моделирования движения грунтовых вод. Эта методика моделирует двухмерный, вертикально перемешанный и устойчивый сток, при котором глубина залегания верхней границы пласта не зависит от его глубины.
Вычисления стока по Дарси
Уравнения для вычисления стока по Дарси подробно описаны в следующих разделах.
Вычисление стока и скорости
Закон Дарси гласит, что скорость Дарси q в пористой среде линейно зависит от гидравлической проводимости K и напорного градиента
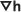(потеря напора на единицу расстояния в направлении движения потока жидкости):- q = -K
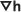
, где значение K может быть вычислено на основании проницаемости T и толщины пласта b, как K = T/b.
Это значение q, единицы измерения которого – объем / время / площадь, также известно как специфический объемный расход, объемный поток или скорость просачивания. Бир (Bear, 1979) определяет его, как объем воды, протекающий за единицу времени через поперечное сечение, перпендикулярное направлению стока.
- q = -K
Тесно связан с объемным потоком поток в водоносном горизонте U, который представляет собой расход воды на единицу ширины водоносного пласта (с единицами измерения объем / время / длина):
- U = -T
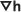
Это построение предполагает, что глубина залегания верхней границы пласта не зависит от глубины, поскольку сток является горизонтальным.
- U = -T
Средняя скорость движения жидкости по порам, именуемая скоростью просачивания V, – это скорость по Дарси, деленная на эффективную пористость среды:
При реализации инструмента Сток по Дарси, это скорость просачивания V, вычисляемая ячейка за ячейкой. Для ячейки i,j поток в водоносном горизонте U вычисляется по каждой из четырёх граней ячейки, используя разницу в заголовках между двумя смежными ячейками и гармоническим средним водопроницаемости Ti+1/2,j (Konikow and Bredehoeft, 1978), которые считаются изотропными.
К примеру x для компонента
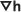уравнение для ячеек i,j и i+1,j будет выглядеть так:- δh/δx ≈ (hi+1 - hi) / Δx
Эта схема проиллюстрирована на следующем рисунке.
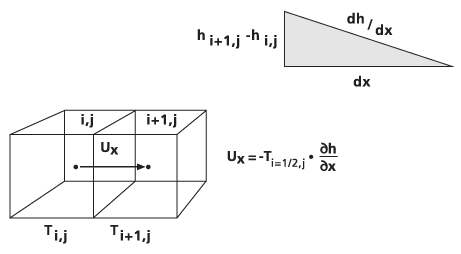
Вычисление остаточного баланса объема грунтовых вод
В приведенном вычислении для стороны ячейки поток в водоносном горизонте между ячейками i,j и i+1,j течет параллельно направлению x и вычисляется как:
Чтобы определить остаточный баланс грунтовых вод, должен быть вычислен объемный расход грунтовых вод через ячейку. Этот расход Q x(i+1/2) вычисляется на основании потока в водоносном пласте U и размера стороны ячейки Δy в соответствии со следующим уравнением:
- Qx(i+1/2,j) = Ux(i+1/2,j) Δy
Аналогичные значения должны быть получены для всех четырех сторон ячейки. Эти значения используются для вычисления остаточного объема подземных вод Rvol для каждой ячейки, который записывается в выходной растр. Значение представляет излишек (или, в случае отрицательного значения, дефицит) воды в каждой ячейке при условии чистого потока, вычисляемое по уравнению:
Этот остаточный объем подземных вод Rvol в идеале должен быть равен нулю для всех ячеек. При изучении выходного растра, содержащего значения остаточного баланса объема, ищет отклонения от нуля. Большие позитивные или негативные остаточные объемы указывают на производство или потерю массы, что нарушает принцип непрерывности и подразумевает несостоятельные данные по глубине залегания верхней границы водоносного пласта и данным по проницаемости. Согласующиеся участки положительных и отрицательных значений остаточного баланса объема позволяют предположить, что на территории существуют неустановленные источники или приемники. Уменьшите значения остаточного баланса объема грунтовых вод до выполнения дальнейшего моделирования. Как правило, для уменьшения значений остаточного баланса исправления вносятся в поле проницаемости.
Вычисление векторов стока
Фактические уравнения, используемые в инструменте Сток по Дарси для вычисления векторов стока для каждой ячейки, получены на основании среднего арифметического Ux(i-1/2,j) и Ux(i+1/2,j), деленного на значение пористости среды в центре ячейки ni,j и на толщину водоносного пласта bi,j для получения значения скорости просачивания Vx в центре ячейки:
и аналогичное уравнение используется для вычисления V y в центре:
Центрирование осуществляется в соответствии с условием, согласно которому хранимые значения соответствуют центрам ячеек. Эти значения преобразуются в направление и величину стока, определяемых в географических координатах, для хранения в выходных растрах направления и величины.
В случае с краевыми ячейками растра, для которых информации недостаточно, значения для скорости просто копируются из ближайшей внутренней ячейки.
Значения пористости
В следующих таблицах собраны некоторые значения пористости и гидравлической проводимости для различных геологических формаций.
Таблица 1: Гидравлические проводимости рыхлых пород
| Средний | K (м/с) |
|---|---|
Крупный гравий | 10-1 - 10-2 |
Песок и гравий | 10-1 - 10-5 |
Тонкий песок, ил, лессы | 10-5 – 10-9 |
Глина, глинистые сланцы, гляциальные отложения | 10-9 - 10-13 |
Таблица 2: Гидравлические проводимости твердых пород
| Средний | K (м/с) |
|---|---|
Доломитовый известняк |
10-3 - 10-5 |
Выветренный мел |
10-3 - 10-5 |
Невыветренный мел |
10-6 - 10-9 |
Известняк |
10-5 – 10-9 |
Песчаник |
10-4 - 10-10 |
Гранит, гнейс, плотный базальт |
10-9 - 10-13 |
Таблица 3: Пористость геологических формаций
| Средний | Общая пористость |
|---|---|
Неизмененный гранит и гнейс | 0.0002 – 0.018 |
Кварцит | 0.008 |
Глинистый сланец, аспидный сланец, слюда | 0.005 – 0.075 |
Известняк, первичный доломит | 0.005 – 0.125 |
Вторичный доломит | 0.10 – 0.30 |
Мел | 0.08 – 0.37 |
Песчаник | 0.035 – 0.38 |
Вулканический туф | 0.30 – 0.40 |
Песок | 0.15 – 0.48 |
Глина | 0.44 – 0.53 |
Разбухающая глина, ил | до 0,90 |
Пахотные почвы | 0.45 – 0.65 |
Дополнительные значения пористости и гидравлической проводимости собраны в таблицах, опубликованных в издании Freeze and Cherry (1979). В работе Gelhar et al. (1992) представлены значения пористости и проводимости различных формаций. Детальное обсуждение пористости в осадочных породах приводится в работе Blatt et al. (1980). Подробно адвективно–дисперсионное моделирование, использующее эти функции, представлено в работе Tauxe (1994).
Примеры
Обычная последовательность при моделировании рассеивания грунтовых вод – запуск инструмента Сток по Дарси, затем инструмента Трек частиц, а затем инструмента Фильтрация в водоносном горизонте.
- Пример параметров для диалогового окна инструмента Сток по Дарси:
Входной растр глубин залегания водоносного пласта : head
Входной растр эффективной пористости : poros
Входной растр толщины водоносного пласта : thickn
Входной растр водопроницаемости : transm
Выходной растр баланса остаточного объема грунтовых вод : resid1
Выходной растр направления : dir1
Выходной растр величины : mag1
- Пример параметров в диалоговом окне для инструмента Скорость по Дарси:
Входной растр глубин залегания водоносного пласта : head
Входной растр эффективной пористости : poros
Входной растр толщины водоносного пласта : thickn
Входной растр водопроницаемости : transm
Выходной растр направления : dir1
Выходной растр величины : mag1
Справочная информация
Bear, J. Hydraulics of Groundwater. McGraw-Hill. 1979
Blatt, H., G. Middleton, and R. Murray. Origin of Sedimentary Rocks, 2nd Ed. Prentice-Hall. 1980
Freeze, R. A., and J. A. Cherry. Groundwater. Prentice-Hall. 1979
Gelhar, L. W., C. Welty, and K. R. Rehfeldt. "A Critical Review of Data on Field-Scale Dispersion in Aquifers". Water Resources Research, 28 no. 7: 1955-1974. 1992.
Konikow, L. F. and J. D. Bredehoeft. "Computer Model of Two-Dimensional Solute Transport and Dispersion in Ground Water", USGS Techniques of Water Resources Investigations, Book 7, Chap. C2, U.S. Geological Survey, Washington, D.C. 1978.
Marsily, G. de. Quantitative Hydrogeology. Academic Press. 1986.
Tauxe, J. D. "Адвективно-дисперсионное моделирование пористой среды в ГИС". Докторская диссертация в области строительства. The University of Texas at Austin, 1994.