Инструмент Кластеризация на основе плотности определяет области концентрации точек, отделяя их от пустых и разреженных областей. Точки, не являющиеся частью кластера, помечаются, как шум. Дополнительно время точек можно использовать для поиска групп точек, которые группируются вместе в пространстве и времени.
Инструмент использует алгоритмы автоматической кластеризации без обучения, автоматически определяющие основанные на пространственном положении расстоянии до заданного числа соседей наборы. Эти алгоритмы называются алгоритмами «без обучения», так как для них не требуется описания того, что такое кластер.
Подсказка:
Кластеризация, группировка и классификация - одни из самых часто используемых.методов машинного обучения. Инструменты Многовариантная классификация и Пространственно ограниченная многовариантная кластеризация также используют методы обработки «без обучения» для нахождения естественных кластеров ваших данных. Эти методы классификации называются классификацией «без обучения», так как не требуют набора классифицированных заранее объектов для «тренировки» алгоритма для дальнейшего поиска кластеров в ваших данных.
Возможное применение
Некоторые способы использования этого инструмента перечислены далее:
- Городские сети водоснабжения - важнейшие подземные структуры. Кластеризация трещин и разрывов в трубах может быть индикатором надвигающихся проблем. С помощью инструмента Кластеризация на основе плотности инженер может найти расположение кластеров и предпринять превентивные меры в зонах повышенной опасности сетей водоснабжения.
- Представьте, что у вас есть координаты мест, с которых были выполнены все удачные и неудачные броски игроков NBA. Инструмент Кластеризация на основе плотности покажет вам зоны удачных и неудачных мест для броска для каждого игрока. Эта информация может оказаться очень полезной для выбора стратегии на матч.
- Допустим, вы изучаете какую-то болезнь, вызванную переносчиками инфекции и у вас есть набор точечных данных о домашних хозяйствах изучаемой области, некоторые из которых являются зараженными, а некоторые - нет. Посредством инструмента Кластеризация на основе плотности можно выделить наибольшие кластеры зараженных переносчиками инфекции домашних хозяйств, чтобы выделить места, в которых нужно начать лечение и уничтожение паразитов.
- Твиты с геолокацией. связанные с природными опасностями или террористическими атаками, могут быть кластеризованы и, на основе размера и местоположения кластеров, получена информация о необходимых мерах по спасению и эвакуации.
Методы кластеризации
Параметр инструмента Кластеризация на основе плотности Метод кластеризации предлагает три опции для поиска кластеров в точечных данных:
- Указанное расстояние (DBSCAN) — Использует указанное расстояние для отделения плотных кластеров от окружающего шума. Алгоритм DBSCAN самый быстрый из методов кластеризации,но применим только в случае, если четко ясно, какое Расстояние поиска использовать для получения хороших результатов для всех потенциальных кластеров. Это происходит в ситуации сходных плотностей всех важных кластеров. Этот метод также позволяет использовать параметры Поле времени и Интервал времени поиска для поиска кластеров точек в пространстве и времени.
- Автонастройка (HDBSCAN) — Использует различные расстояния для отделения кластеров с различными плотностями от окружающего шума. HDBSCAN является наиболее ориентированным на данные методом кластеризации, для него требуется минимум участия пользователя.
- Мультимасштабный (OPTICS) — Использует расстояние между соседними объектами для создания графика достижимости, который применяется для отделения кластеров различных плотностей от шума. OPTICS предлагает наибольшую гибкость в тонких настройках определения кластеров, хотя и требует интенсивных вычислений, особенно с большим Расстоянием поиска. Этот метод также позволяет использовать параметры Поле времени и Интервал времени поиска для поиска кластеров точек в пространстве и времени.
Этот инструмент принимает на входе Входные точечные объекты, путь к Выходным объектам и значение минимального числа объектов, которые будут считаться кластером. В зависимости от Метода кластеризации могут быть дополнительные параметры, как, например, показано ниже.
Минимальное число объектов на кластер
Этот параметр определяет минимальное количество объектов, которые могут быть сгруппированы в кластер. Например, если у вас несколько различных кластеров размером от 0 до 100 точек и вы выберете Минимальное количество объектов для кластера равным 20, все кластеры размером менее 20 будут либо считаться шумом (так как не формируются в кластер подходящего размера), либо будут слиты с соседними кластерами, чтобы минимальное количество объектов было соблюдено. Напротив, задав значение Минимального числа объектов в кластере меньше, чем предполагаемый вами размер наименьшего значимого кластера, вы можете добиться разбиения этих кластеров на меньшие. Другими словами, чем меньше Минимальное число объектов в кластере, тем больше кластеров будет обнаружено. Чем больше Минимальное число объектов в кластере, тем меньше кластеров будет обнаружено.
Подсказка:
Идеальное значение Минимального числа объектов в кластере зависит от того, чего вы пытаетесь добиться и в чем цель вашего анализа. Оно должно соответствовать минимальному размеру, который будет считаться значимым кластером. Увеличение Минимального числа объектов в кластере может привести к слиянию некоторых небольших кластеров.
Параметр Минимальное число объектов в кластере также является очень значимым для вычисления кластерного расстояния, которое применяется всеми тремя методами нахождения кластеров. Концептуально кластерное расстояние для каждой точки - это дистанция, требуемая для достижения каждой точкой заданного минимального числа объектов. Если выбрано большое значение Минимального числа объектов в кластере, соответственно, и кластерное расстояние будет большим. Если выбрано маленькое значение Минимального числа объектов в кластере, то и кластерное расстояние будет небольшим. Кластерное расстояние связано с параметром Расстояние поиска, использующимся методами Заданное расстояние (DBSCAN) и Многомасштабный (OPTICS).
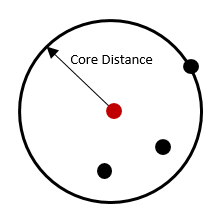
Расстояние поиска (DBSCAN и OPTICS)
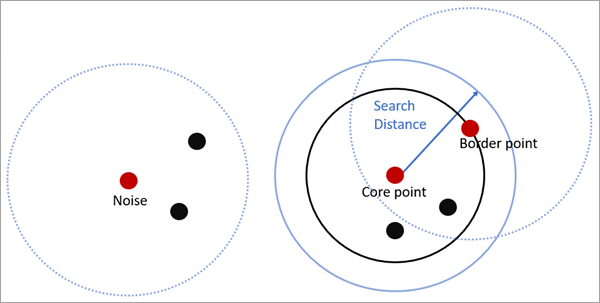
Для метода Заданное расстояние (DBSCAN) в случае, если Минимальное число объектов в кластере не может быть найдено в пределах Расстояния поиска от конкретной точки, такая точка помечается, как основная точка и включается в кластер вместе со всеми точками в пределах кластерного расстояния. Граничная точка - это точка, которая находится в пределах расстояния поиска от точки кластера, но сама не имеет минимального количества объектов в пределах расстояния поиска. Каждый результирующий кластер состоит из основных и граничных точек, где основные точки имеют тенденцию попадать в середину кластера, а граничные точки на внешнюю часть. Если точка не имеет минимального количества объектов в пределах расстояния поиска и не находится в пределах расстояния поиска другой основной точки (другими словами, это не основная точка и не граничная точка), она помечается как точка шума и не входит ни в один кластер.
Для метода Мультимасштабный (OPTICS) значение Расстояние поиска, рассматривается, как максимальное расстояние, сравниваемое с кластерным расстоянием. Метод Мультимасштабный (OPTICS) использует концепцию максимально достижимого расстояния, являющегося расстоянием от точки до ее ближайшего соседа, еще не появлявшегося в поиске. (Помните: OPTICS i - упорядоченный алгоритм, начинающий работу с объекта с минимальным ID и переходит от этой точки к следующей точке для создания графика. Порядок точек влияет на результаты его работы.) Метод Многомасштабный (OPTICS) будет проверять все соседние расстояния в пределах заданного Расстояния поиска, сравнивая каждое из них с кластерным расстоянием. Если какое-то расстояние окажется меньше кластерного, то объекту присваивается это кластерное расстояние в качестве достижимого. Если все расстояния оказываются большими, чем кластерное расстояние, наименьшее из них считается достижимым. Когда в пределах расстояния поиска больше нет точек, процесс перезапускается с новой точки, которая ранее не появлялась в поиске. В каждой итерации пересчитываются и сортируются расстояния достижимости. Наименьшее из расстояний используется для определения конечного расстояния достижимости каждой точки. Эти расстояния достижимости затем используются для создания графика достижимости, являющегося упорядоченным графиком расстояний достижимости, который применим для определения кластеров.
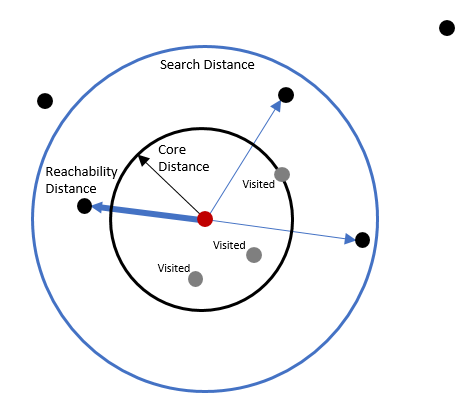
Для обоих методов, Заданное расстояние (DBSCAN) и Мультимасштабный (OPTICS), по умолчанию Расстоянием поиска является наибольшее значение кластерного расстояния, найденное в наборе данных, исключая те, которые попадают в верхние 1% (т.е., исключая наивысшие значения кластерного расстояния).
Кластеризация в пространстве и времени (DBSCAN и OPTICS)
В двух методах кластеризации время каждой точки может быть указано в параметре Поле времени. Если задано, то инструмент будет искать кластеры точек, которые находятся близко друг к другу в пространстве и времени. Параметр Интервал времени поиска аналогичен расстоянию поиска и используется для определения основных точек, граничных точек и точек шума пространственно-временных кластеров.
Для метода Заданное расстояние (DBSCAN), при поиске участников кластера, Минимальное число объектов на кластер должно быть найдено в значениях Расстояние поиска и Интервал времени поиска, чтобы быть центральной точкой пространственно-временного кластера.
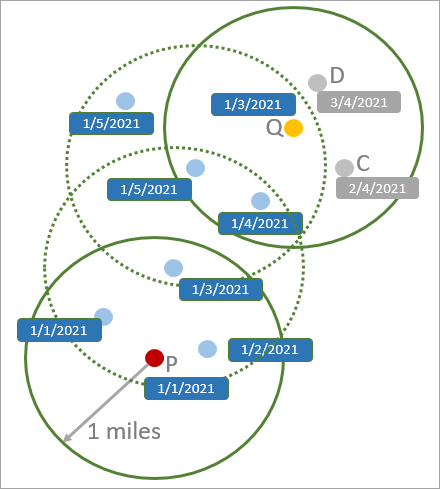
На следующем изображении расстояние поиска составляет 1 милю, интервал времени поиска 3 дня, а минимальное количество объектов 4. Точка P является основной, потому что есть четыре точки в пределах расстояния поиска и временного интервала (включая саму себя). Точка Q является граничной, потому что есть только три точки в пределах расстояния поиска и временного интервала, но эта точка находится в пределах расстояния поиска и временного интервала от основной точки кластера (точка с отметкой времени 1/5/2021). Точки C и D являются точками шума, потому что они не являются ни основными, ни граничными точками кластера, а все другие точки (включая P и Q) образуют единый кластер.
Для метода Мультимасштабный (OPTICS) все точки за пределами Интервала времени поиска будут исключены, при этом для точки вычисляется ее кластерное расстояние, ищутся все расстояния до соседей в рамках указанного значения Расстояние поиска и вычисляется расстояние достижимости.
На следующем изображении расстояние поиска составляет 2 мили, интервал времени поиска 3 дня, а минимальное количество объектов 4. Кластерное расстояние для точки P вычисляется с пропуском точки q3, поскольку она находится за пределами интервала времени поиска. В этом случае кластерное расстояние для P равно расстоянию достижимости для P.
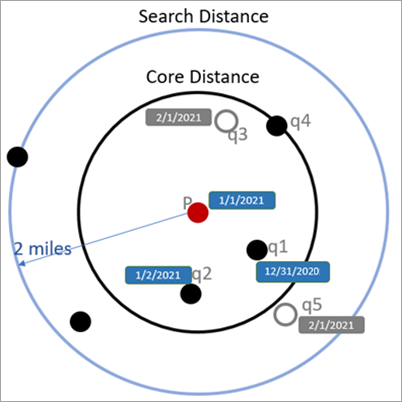
На следующем изображении показано вычисление расстояния достижимости, когда некоторые соседние точки уже были просмотрены. Точки q1, q2 и q4 были пропущены, потому что они были ранее просмотрены, а точки q3 и q5 были пропущены, потому что они находятся за пределами окна временного поиска.
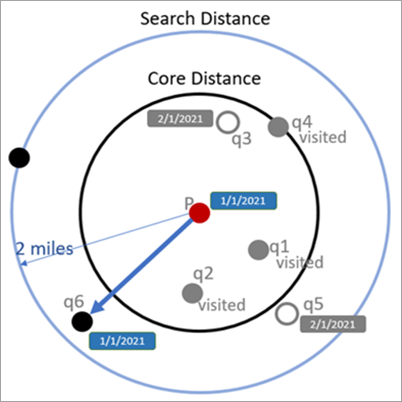
График достижимости (OPTICS)
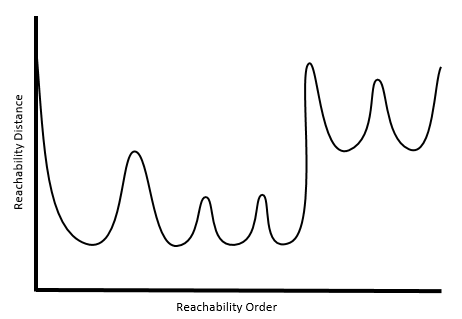
После того как будут вычислены все расстояния достижимости набора данных, создается график достижимости, упорядочивающий расстояния и показывающий кластерную структуру точек.
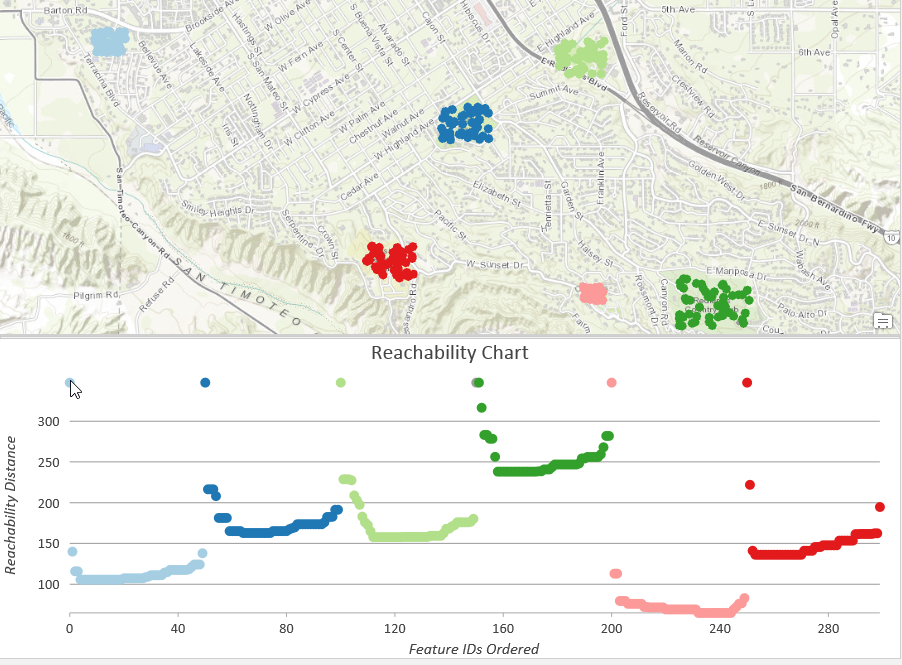
Понижения графика означают, что между точками небольшое расстояние. То есть эти участки соответствуют кластерам точек. Чем более плотным является кластер, тем меньше будут расстояния достижимости и тем глубже будет впадина на графике (например, розовый кластер - самый плотный в показанном выше примере). У менее плотных кластеров большие расстояния доступности и более высокие области на графике (например, темно-зеленый кластер - наименее плотный в показанном выше примере). Пики отображают расстояния, необходимые для перемещения от кластера к кластеру либо от кластера до шума и снова до кластера - в зависимости от конфигурации набора точек.
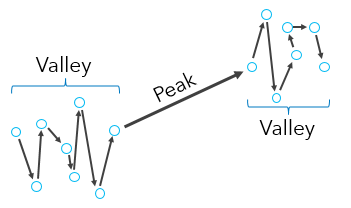
Плоские области появляются, если Расстояние поиска меньше наибольшего кластерного расстояния. Ключевым моментом использования метода кластеризации OPTICS является способ определения кластеров на графике достижимости, контролирующийся параметром Чувствительность кластера.
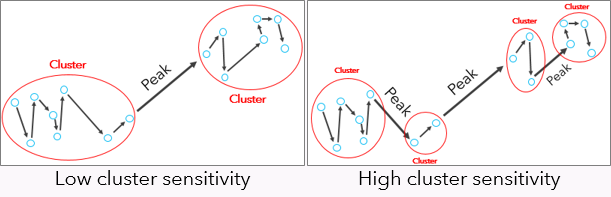
Чувствительность кластера
Параметр Чувствительность кластера определяют, как форма пиков (и уклон, и высота) на графике достижимости будет использоваться для разделения кластеров. Очень высокое значение Чувствительности кластера (близкое к 100) приведет к рассмотрению даже минимального пика в качестве разделения между кластерами, в результате чего будет получено очень большое их количество. Очень низкая Чувствительность кластера (близкое к 0) будет рассматривать в качестве границ для кластеров только наиболее крутые и высокие пики, что приводит к меньшему количеству кластеров.
По умолчанию Чувствительность кластера вычисляется, как допуск, при котором при добавлении новых кластеров не появляется дополнительной информации, вычисляется, как Дивергенция Кулбака-Лейблера между исходным графиком достижимости и сглаженным графиком достижимости, полученным после кластеризации.
Сравнение методов интерполяции
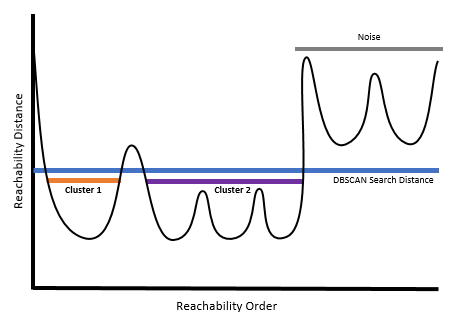
Хотя только алгоритм Мультимасштабный (OPTICS) применяет для определения кластеров график достижимости, этот график может использоваться для иллюстрации отличий методов друг от друга. Для данной иллюстрации представленный далее график достижимости будет использован для объяснения различий трех методов. На графике отображены кластеры различной плотности и разных расстояний разделения. Мы с помощью этого изображения изучим результаты использования каждого из методов кластеризации.
Для Заданного расстояния (DBSCAN) представьте себе линию, пересекающую график на указанном Расстоянии поиска. Области под Расстоянием поиска соответствуют кластерам, а пики над Расстоянием поиска - точкам шума. Заданное расстояние (DBSCAN) - самый быстрый из методов кластеризации, но он применим только в случае, если четко ясно, какое Расстояние поиска использовать и это Расстояние поиска подходит для всех потенциальных кластеров. Это происходит в ситуации сходных плотностей всех важных кластеров.
Для Самонастраивающегося (HDBSCAN) алгоритма расстояния достижимости можно рассматривать как вложенные уровни кластеров. Каждый уровень кластеризации приведет к обнаружению разных наборы кластеров. Самонастраивающийся (HDBSCAN) алгоритм выбирает, на каком уровне кластеров в каждом наборе вложенных кластеров будут созданы наиболее стабильные кластеры, включающие максимально возможное количество объектов и не содержащие шумов. Подробнее об алгоритме см. в прекрасной документации от создателей HDBSCAN. Самонастраивающийся (HDBSCAN) является наиболее ориентированным на данные методом кластеризации, для него требуется минимум участия пользователя.
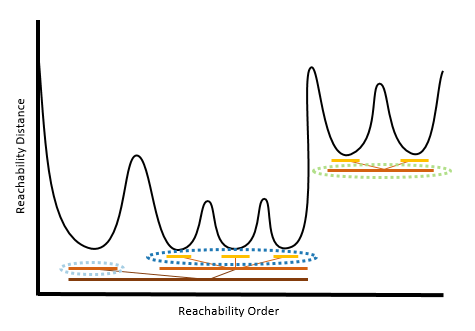
В алгоритме Мультимасштабный (OPTICS) определение кластеров основывается не на конкретном расстоянии, а на пиках и впадинах графика. Предположим, что у пика есть уровни: малый, средний и большой.
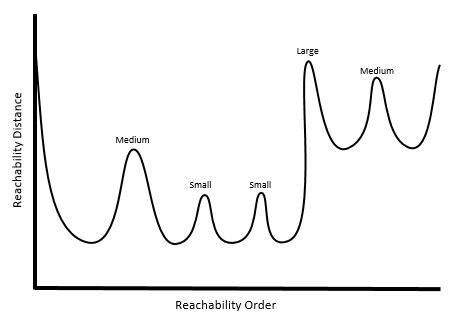
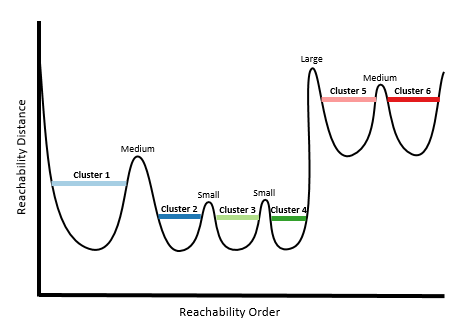
Выбор очень высокой Чувствительности кластера, по сути, означает, что все пики, от малых до больших, будут действовать как разделители между кластерами (что приводит к большому числу классов).
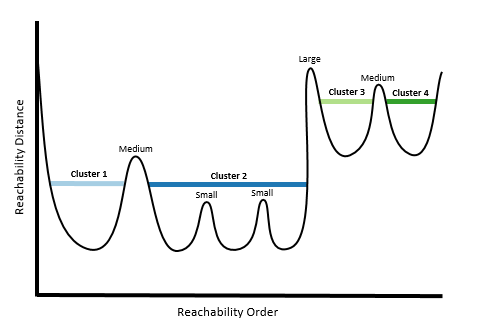
При выборе средней Чувствительности кластеров будут использоваться только Большие и Средние пики, а малые - нет.
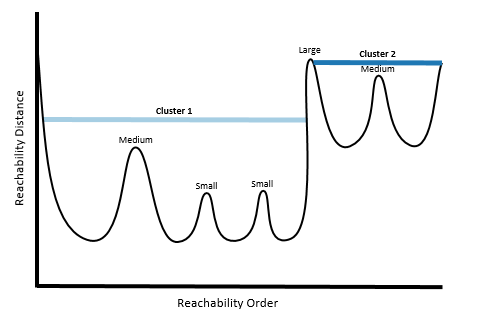
При выборе низкой Чувствительности кластеров будут использоваться только Большие пики, в результате чего будет обнаружено наименьшее число кластеров.
Мультимасштабный (OPTICS) предлагает наибольшую гибкость в тонких настройках определения кластеров, хотя и является самым медленным из трех методов кластеризации.
Результаты
Этот инструмент создает выходной класс объектов с новым целочисленным полем CLUSTER_ID, где обозначается принадлежность объектов кластерам. Отображение по умолчанию основано на поле COLOR_ID. Разным кластерам присваиваются различные цвета. Цвета распределяются и повторяются таким образом, что каждый кластер визуально отличается от соседних.
Если Методом кластеризации выбран Автонастройка (HDBSCAN), выходной класс объектов также будет содержать следующие поля: PROB, в котором хранится вероятность принадлежности объекта к группе, OUTLIER, означающее, что объект может быть выбросом в своем кластере (чем выше значение, тем больше вероятность, что объект является выбросом) и EXEMPLAR, где обозначаются объекты, наиболее характерные для данного кластера.
Этот инструмент также создает сообщения и диаграммы, помогающие понять характеристики найденных кластеров. Вы можете получить доступ к сообщениям, наведя курсор мыши на индикатор выполнения, щелкнув на кнопку всплывающего окна и развернув раздел Сообщения на панели Геообработка. Вы также можете открыть сообщения, касающиеся ранее запущенного инструмента Кластеризация на основе плотности через панель История геообработки. Созданные диаграммы можно открыть с помощью панели Содержание.
Помимо создающегося при работе алгоритма Мультимасштабный (OPTICS) графика достижимости, все методы кластеризации создают столбчатую диаграмму со всеми уникальными значениями Cluster ID. Эту диаграмму можно использовать для быстрого выбора всех объектов, попадающих внутрь заданного кластера и изучения размера кластеров.
Дополнительные ресурсы
Подробнее о DBSCAN:
- Birant, D. & Kut, A. (2007, January). "ST-DBSCAN: An algorithm for clustering spatial–temporal data." В Data & Knowledge Engineering (Том 60, N. 1, стр. 208-221). https://doi.org/10.1016/j.datak.2006.01.013
- Ester, M., Kriegel, H. P., Sander, J., & Xu, X. (1996, Август). "A density-based algorithm for discovering clusters in large spatial databases with noise." В Kdd (Том 96, N 34, стр. 226-231).
Подробнее о HDBSCAN:
- Campello, R. J., Moulavi, D., & Sander, J. (2013, Апрель). "Density-based clustering based on hierarchical density estimates." В Pacific-Asia Conference on Knowledge Discovery and Data Mining (стр. 160-172). Springer, Berlin, Heidelberg.
Подробнее о OPTICS:
- Agrawal, K. P., Garg, S., Sharma, S., & Patel, P. (2016, Ноябрь). "Development and validation of OPTICS based spatio-temporal clustering technique." В Information Sciences (Том 369, стр. 388-401). https://doi.org/10.1016/j.ins.2016.06.048.
- Ankerst, M., Breunig, M. M., Kriegel, H. P., & Sander, J. (1999, Июнь). "OPTICS: ordering points to identify the clustering structure." В ACM Sigmod record (Том 28, N. 2, стр. 49-60). ACM.