Доступно с лицензией Geostatistical Analyst.
Чтобы удалить из данных поверхностный тренд и использовать кригинг или кокригинг на остальных данных без тренда, можно воспользоваться аддитивной моделью:
Z(s) = µ(s) + ε(s),где µ(s) ― это некая детерминированная поверхность (тренд), а ε(s) ― это пространственно автокоррелированная ошибка.
Теоретически, тренд неизменен, а это значит, что если вы будете моделировать данные снова и снова, этот тренд никогда не изменится. Однако вы увидите отклонения в смоделированных поверхностях из-за наличия случайных ошибок автокорреляции. Тренд обычно меняется в пространстве постепенно, а случайные ошибки меняются гораздо быстрее. В качестве примера наблюдаемого (и известного в теории) градиента температуры, меняющейся с изменением высоты, можно привести метеорологические данные. Однако наблюдения в определенный день показывают локальные изменения из-за атмосферных фронтов, подстилающего земельного покрова, облачности и так далее, которые являются менее предсказуемыми, поэтому в модели для локальных колебаний выполняется автокорреляция.
К сожалению, идеального способа разложить данные на только трендовые и случайные ошибки не существует. Далее приводится возможный вариант решения этой задачи.
На следующей диаграмме удаления тренда данные имитировались из двух моделей. Одной из них была модель ординарного кригинга, где Z(s) = µ + ε(s), и эти ошибки были связаны с автокорреляцией. Процесс имел среднее µ = 0 с экспоненциальной вариограммой. Другой набор данных был смоделирован из модели универсального кригинга, где µ(s) = ß0 + ß1x(s) + ß2x2(s); она показана сплошной линией, но эти ошибки были независимыми со средним 0 и дисперсией 1.
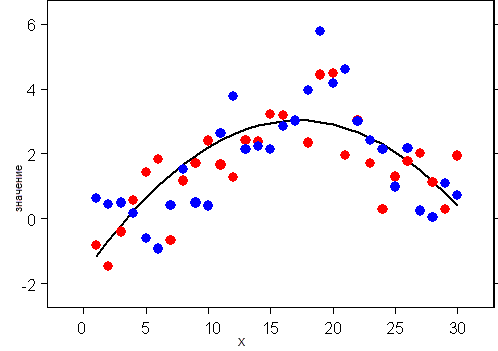
Трудно различить, какая из моделей какой является (синие круги - модель ординарного кригинга, красные - модель универсального кригинга с независимыми ошибками). С помощью пространственной автокорреляции можно создавать гибкие прогнозируемые поверхности, а этот пример показывает, что сложно бывает выбрать между моделями, если учитывать только данные. В целом, следует использовать ординарный кригинг, если только нет обоснованных причин удалять поверхность тренда. Делать это следует потому, что модели должны быть как можно более простыми. Если удалить поверхность тренда, будет больше параметров для анализа. Двухмерная квадратичная поверхность добавляет к параметру деления еще пять параметров, которые необходимо будет проанализировать. Чем большее количество параметров анализируется, тем менее точной становится модель.
Однако могут быть случаи, когда пространственные координаты выступают посредником к определенному известному тренду в данных. Например, урожайность может меняться с широтой. Не из-за самих координат, а потому что температура, влажность, количество осадков и так далее меняются с изменением широты. В таких случаях может быть полезно удалить поверхности тренда. Опять же, поверхности должны быть как можно более простыми, такими, как полиномы первого или второго порядка.
При использовании трендов существует опасность переборщить с подгонкой данных и оставить слишком мало вариаций в остатках, чтобы должным образом учесть неопределенность прогноза. При использовании моделей тренда всегда следует выполнять обычную или перекрестную проверку моделей.
Вы также можете использовать инструмент Направленный тренд для визуализации тренда в различных направлениях, что поможет выбрать подходящую модель удаления тренда. Попробуйте различные направления и полиномы различного порядка, чтобы понять, как меняется тренд в разных направлениях.

Более подробно о преобразованиях и трендах