Доступно с лицензией Geostatistical Analyst.
Интерполяция по методу глобального полинома соответствует ровной поверхности, задаваемой математической функцией (полиномом) для входных точек выборки. Поверхность глобального полинома постепенно изменяется и охватывает шаблоны грубых масштабов в данных.
Концептуально интерполяция по методу глобального полинома сходна с установкой листа бумаги между поднятыми точками (поднятыми до высоты значения). Это показано на диаграмме ниже для набора точек образца высот, взятых на холме с небольшим уклоном (лист бумаги показан пурпурным).

Но плоский лист бумаги не будет точно охватывать ландшафт, содержащий долину. Однако, если вам можно согнуть лист бумаги один раз, вы получите гораздо лучшее соответствие. Добавление члена в математическую формулу дает аналогичный результат, сгиб плоскости. Плоская поверхность (нет сгиба на листе бумаги) – это полином первого порядка (линейный). Допустим, что один перегиб – это полином второго порядка (квадратический), два перегиба – полином третьего порядка (кубический) и т.д. до поддерживаемого в Geostatistical Analyst десятого порядка. На следующем рисунке концептуально показан полином второго порядка, соответствующий долине.
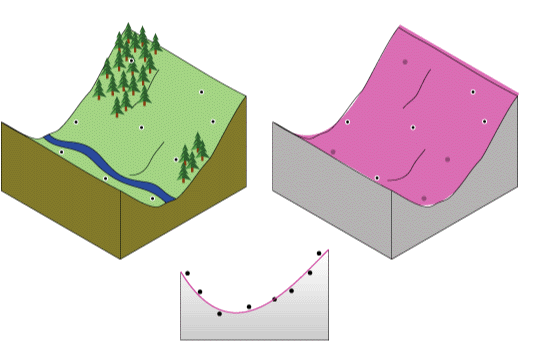
Редко лист бумаги проходит через фактически измеренные точки, таким образом делая интерполяцию по методу глобального полинома неточным методом интерполяции. Некоторые точки будут расположены выше листа бумаги, другие – ниже. Однако, если вы добавите высоту до высоты точек выше листа бумаги, а также добавите высоту для точек ниже листа бумаги, эти две суммы должны быть равны. Поверхность, показанная пурпурным цветом, получается путем использования подходящей регрессии наименьших квадратов. Результирующая поверхность сводит к минимуму различия между квадратами поднятых значений и листом бумаги.
Случаи использования интерполяции по методу глобального полинома
Результатом интерполяции по методу глобального полинома является сглаженная поверхность, которая представляет постепенные тренды поверхности в исследуемой области.
Интерполяция по методу глобального полинома используется в следующих целях:
- Подгонки поверхности к точкам образца, если поверхность варьируется постепенно от участка к участку исследуемой области, например, загрязнение окружающей среды в промышленной зоне.
- Исследования или удаления эффектов трендов с большим диапазоном или глобальных трендов. При таких обстоятельствах, метод часто называют анализ поверхности тренда.
Интерполяция по методу глобального полинома создаёт постепенно изменяющуюся поверхность с помощью полиномов низкого порядка, которые могут описывать физический процесс (например, загрязнение и направление ветра). Но помните о том, что чем более сложным будет полином, тем труднее будет приписать ему физический смысл. Кроме того, вычисленные поверхности весьма чувствительны к выпадающим значениям (чрезвычайно высоким и низким значениям), особенно на ребрах.