Расстояние между любыми двумя объектами рассчитывается как кратчайшая дистанция между ними, когда два объекта находятся ближе всего друг к другу. Эту логику применяет любой инструмент геообработки, который вычисляет расстояние, включая такие инструменты, как Ближайший объект, Построить таблицу соседних объектов и Пространственное соединение (с опцией Ближайший).
Измерения расстояний будут наиболее точными, если входные данные находятся в равнопромежуточной проекции. Хотя вычисление расстояний можно выполнить всегда - независимо от системы координат, - результаты могут оказаться неточными или даже абсурдными, если ваши данные находятся в географической системе координат или неправильно выбранной системе координат проекции.
Более подробно о картографических проекциях и системах координат
В дальнейшем обсуждении расстояние всегда будет означать наименьшее расстояние между двумя объектами.
Особые примечания
Необходимо учитывать следующее:
- Несколько объектов могут располагаться одинаково близко по отношению к другому. Когда это происходит, один из одинаково близких объектов будет случайным образом выбран в качестве ближайшего.
- Когда один объект содержит в себе другой или находится внутри него, расстояние между ними равно нулю.
- Это означает, что когда объект находится внутри полигона, расстояние между объектом и окружающим его полигоном равно нулю.
- Расстояние между двумя объектами считается равным нулю, если у них есть хотя бы одна общая координата x, y.
- Это значит, что когда два объекта пересекаются, накладываются друг на друга, перекрещиваются или касаются друг друга, расстояние между ними равно нулю.
- Расстояние всегда вычисляется до границы полигонального объекта, а не до его центра или центроида.
- Как отмечалось выше, если объект полностью находится внутри полигона, расстояние между объектом и окружающим его полигоном равно нулю.
- Расстояние между двумя объектами (любого типа) всегда одинаково, независимо от того, от какого и до какого объекта ведется измерение.
Базовые операции нахождения расстояния
Расчет расстояния зависит от типа геометрии объектов, а также от других факторов, например, от системы координат. Но существуют три основных правила, которые подробно описаны ниже и определяют, как рассчитывается расстояние.
- Расстояние между двумя точками является прямой линией, соединяющей их.
- Расстояние от точки до прямой равно либо длине перпендикуляра, либо расстоянию до ближайшей вершины прямой.
- Расстояние между полилиниями определяется вершинами сегментов.
Правило 1: Расстояние между двумя точками определяется прямой линией, соединяющей их.
На следующем рисунке показано расстояние между двумя точками, а также несколько других ключевых слов и функций, используемых инструментами близости.

Ключевые слова в приведенных выше выносках (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) — это поля, добавляемые к выходным данным инструмента Построить таблицу соседних объектов и к входному классу объектов при запуске инструмента Ближайший.
Мультиточка в мультиточку
Для особого случая вычисления расстояний между многоточечными объектами расстояния от каждой точки входного многоточечного объекта до каждой точки ближайшего мультиточечного объекта вычисляются по правилу 1, и наименьшее из этих расстояний будет являться расстоянием между двумя мультиточечными объектами.
Кроме того, если одна из точек мультиточечного объекта находится над одной из точек другого многоточечного объекта, расстояние между двумя мультиточечными объектами будет равно нулю. Это относится ко всем мультиточечным объектам.
Правило 2: Расстояние от точки до полилинии равно либо длине перпендикуляра, либо расстоянию до ближайшей вершины
В ArcGIS линейные объекты называются полилиниями. Эти два термина — линия и полилиния — являются взаимозаменяемыми. Полилиния представляет собой упорядоченный набор точек, которые называются вершинами. Каждая точка на линии называется вершиной. У полилинии может быть любое число вершин. Линия, задаваемая двумя вершинами, называется сегментом линии или просто сегментом. Две вершины, задающие сегмент линии, называются конечными вершинами.
Точно так же, полигон — это замкнутая область, задаваемая одной или несколькими полилиниями.
Кратчайшее расстояние от точки до сегмента линии — это длина перпендикуляра к этому сегменту. Если через конечные вершины сегмента линии невозможно провести перпендикуляр, кратчайшим расстоянием будет расстояние до ближайшей конечной вершины.
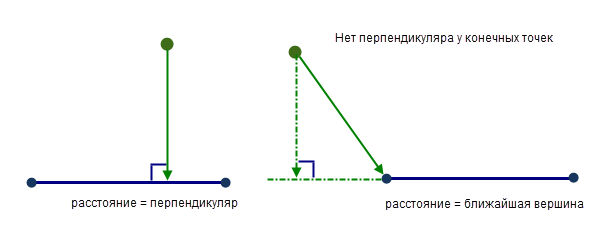
От точки до полилинии
Если у полилинии только один сегмент, для определения расстояния будет применяться Правило 2.
Если полилиния состоит из нескольких сегментов (наиболее распространенный случай), сначала определяется ближайший к точке сегмент линии, а затем применяется Правило 2 для получения расстояния.
От точки до полигона
Поскольку полигон представляет собой область, ограниченную упорядоченным набором линейных сегментов, вычисление расстояния от точки до полигона включает в себя определение ближайшего к точке сегмента линии, а затем применение Правила 2 для получения расстояния.
Расстояние положительно только тогда, когда точка находится вне полигона; в противном случае оно равно нулю.

На приведенном выше изображении расстояние равно нулю для точек 2 и 3 и положительно для точек 1 и 4.
Правило 3: Расстояние между полилиниями определяется вершинами сегментов линий.
Для двух неточечных объектов, таких как два отрезка линии:
- Расстояние от каждой из конечных вершин входного сегмента до ближайшего сегмента рассчитывается с использованием правила 2.
- Вычисляется расстояние от каждой из конечных вершин ближайшего сегмента до входного сегмента.
От полилинии до полилинии
В простейшем случае предположим, что оба полилинейных объекта имеют по одному сегменту каждый. На рисунке ниже показан перпендикуляр CX из вершины C к отрезку, определяемому вершинами AB. Перпендикуляр из вершины D также можно вычислить, но его расстояние больше CX. аким образом, CX — кратчайшее расстояние от сегмента CD до сегмента AB.
Обратите внимание, что из вершины A или B нельзя провести перпендикуляр к отрезку CD, поэтому кратчайшее расстояние вычисляется от вершин A и B до вершины C. В результате получается, что AC — кратчайшее расстояние от сегмента AB до сегмента CD.
Из двух вычисленных расстояний (AC и CX) CX является кратчайшим расстоянием между двумя сегментами, поскольку является наименьшим из всех расстояний от вершины до сегмента.

Если обе полилинии содержат несколько сегментов, находятся два ближайших сегмента, а расстояние между ними рассчитывается согласно Правилу 3.
От полилинии до полигона
При вычислении расстояния между полилинией и полигоном определяются два ближайших сегмента: один сегмент полилинии и один из последовательности сегментов, составляющих границу полигона. Расстояние между этими двумя сегментами вычисляется в соответствии с процессом, описанным в Правиле 3.
Краткая информация
На следующей диаграмме представлена общая картина того, как рассчитываются расстояния между различными типами объектов, а также того, где могут находиться ближайшие местоположения, как описано выше. Показаны не все возможные комбинации.
