Ниже приведены доступные распределения для различных инструментов, которые создают случайные значения. Распределения преобразуют случайные значения 0-1, созданные из заданного потока (идентифицируемые либо глобально в среде анализа, либо локально в инструменте), в заданное распределение. См. Синтаксис распределения для произвольных значений для синтаксиса и параметров для каждого распределения.
Равномерное распределение
Равномерное распределение - это непрерывное распределение вероятностей, при котором все значения в пределах заданного интервала имеют одинаковую вероятность. Целочисленное распределение - это дискретная версия равномерного распределения (см. ниже). Равномерное распределение можно использовать при моделировании концентрации газа в имитационной модели или времени между авариями на перекрестке, а также для размещения точек в инструменте Создать произвольно расположенные точки.
Равномерное распределение часто используется для моделирования случайных событий, когда каждый потенциальный исход или происшествие имеет равную вероятность наступления.
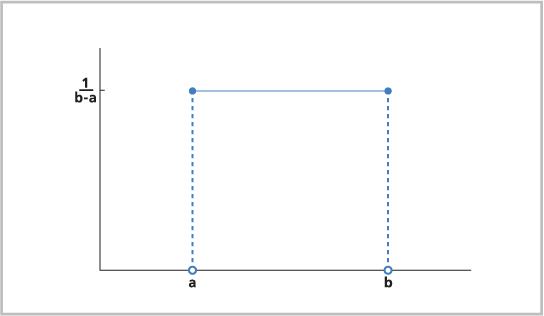
Формула для равномерного распределения выглядит следующим образом:

где
a - минимальное значение для интервала с равной вероятностью.
b - максимальное значение для интервала с равной вероятностью.
x - наблюдения.
Выбранные случайные значения находятся в диапазоне от минимального до максимального (исключая оба). Минимальное значение должно быть меньше максимального. Если минимальные и максимальные значения не указаны, то создаются однородные переменные в диапазоне от 0.0 до 1.0.
Целочисленное распределение
Целочисленное распределение - это распределение вероятностей, при котором все дискретные значения в пределах заданного интервала имеют одинаковую вероятность. Целочисленное распределение - это дискретная версия равномерного распределения (см. выше). Целочисленное распределение может быть использовано для моделирования вероятности выпадения каждого числа при броске кубика (вероятность выпадения каждого числа составляет одну шестую), моделирования случайных событий в имитационной модели или выбора мест отбора проб для биологического исследования.
Целочисленное распределение часто используется для моделирования случайных событий, когда каждый потенциальный исход или происшествие имеет равную вероятность наступления.
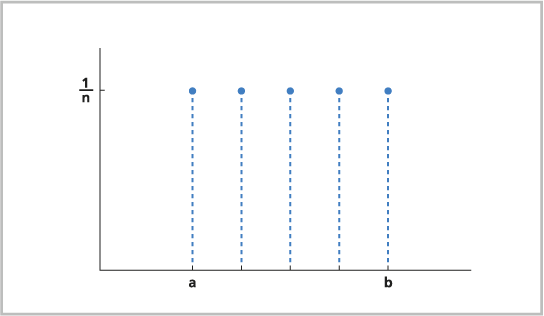
Ниже приведена формула целочисленного распределения:

где
a - минимальное значение для интервала с равной вероятностью.
b - максимальное значение для интервала с равной вероятностью.
x - наблюдения.
Выбранные случайные значения находятся в диапазоне от минимального до максимального (исключая оба). Минимальное значение должно быть меньше максимального. Если минимальные и максимальные значения не указаны, то создаются однородные значения в диапазоне от 1 до 100.
Нормальное распределение
Нормальное распределение моделирует непрерывные случайные величины, которые встречаются часто. Нормальное распределение широко используется и применимо во многих приложениях. Оно построено на центральной предельной теореме, которая основана на принципе, что сумма случайных величин нормально распределяется при наличии большого количества наблюдений. Например, количество выпадений орла в последовательности подбрасываний монеты приблизится к нормальному, если монету подбрасывать много раз. Примерами нормального распределения являются рост людей в стране, значения высоты над уровнем моря в штате и результаты тестов по математике для всех 12-летних учащихся.
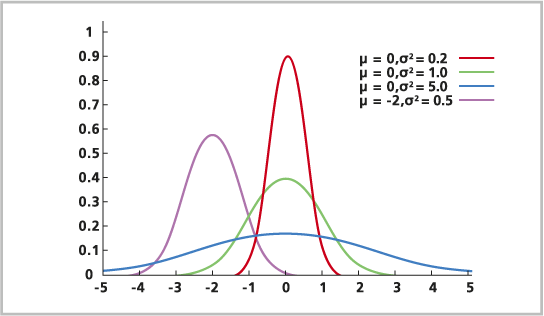
Формула нормального распределения выглядит следующим образом:
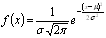
где
μ - среднее.
σ - среднеквадратическое отклонение (положительное число).
Нормальное распределение симметрично относительно среднего, моды и медианы, которые равны в точке μ.
Часто биномиальное распределение и распределение Пуассона моделируют будущие дискретные, независимые, случайные, истинные или ложные события (например, количество выпадений орла при подбрасывании монеты), используя относительно небольшое число наблюдений, в то время как нормальное распределение моделирует непрерывные переменные (например, рост, вес и количество), используя большое количество наблюдений. Биномиальное распределение и распределение Пуассона основаны на вероятности, в то время как нормальное распределение - это количество наблюдений, соответствующих величине.
Экспоненциальное распределение
Экспоненциальное распределение - это непрерывное распределение вероятностей. Обычно оно используется для моделирования времени между событиями, которые происходят с постоянной средней скоростью, или распределение может быть использовано для моделирования возникновения событий на единицу расстояния. Время до следующей автомобильной аварии на перекрестке, время между тем, как в ночном небе появятся две падающие звезды, и расстояние между выбоинами на улице - все это примеры, в которых можно использовать экспоненциальное распределение. В каждом из этих примеров, по мере увеличения времени или расстояния, вероятность изменения состояния или наступления события возрастает в геометрической прогрессии. Эти события происходят независимо друг от друга.

Формула экспоненциального распределения выглядит следующим образом:
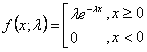
где
e - натуральный логарифм.
x - это возможное количество повторений события (целые положительные значения).
Экспоненциальное распределение моделирует пуассоновские процессы, в которых явление находится в начальном состоянии. Экспоненциальное распределение - это непрерывная версия геометрического распределения. Если процесс перехода из состояния A в состояние B можно разбить на несколько независимых задач, возможно, было бы лучше смоделировать его с помощью гамма-распределения. Гамма-распределение моделирует сумму множества независимых, экспоненциально распределенных переменных. Это можно рассматривать как частный случай экспоненциального распределения.
Распределение Пуассона
Распределение Пуассона - это дискретное распределение вероятностей. Распределение Пуассона моделирует вероятность того, что количество событий произойдет за фиксированный промежуток времени с учетом известного среднего значения. События не зависят от того, когда они происходили в последний раз. По оси x отложены дискретные значения событий 0, 1, 2, 3, 4, и так далее (часто представляющие количество раз, когда происходит событие), а по оси y - вероятность того, что явление произойдет много раз, при известном среднем значении. Этими событиями могут быть количество аварий на перекрестке, количество врожденных дефектов или количество лосей на квадратный километр. Распределение Пуассона моделирует редкие случаи. Это распределение иногда называют законом малых чисел, потому что такое событие случается нечасто, но есть много возможностей для его возникновения.

Формула показана ниже:

где
e - натуральный логарифм.
k - это возможное количество повторений события (целые положительные значения).
k! - это факториал k.
λ (или среднее) - это положительное число, представляющее ожидаемое количество событий в течение заданного интервала. Если событие происходит каждые 10 минут в течение часа (60 минут), значение лямбда будет равно 6.
Распределение Пуассона аналогично биномиальному распределению; однако распределение Пуассона моделирует возникновение редкого события, не имея информации об общем числе возможных событий. Распределение Пуассона исследует количество аварий на перекрестке, в то время как биномиальное распределение моделирует количество аварий в зависимости от количества автомобилей, проезжающих через перекресток.
Гамма-распределение
Гамма-распределение - это непрерывное распределение вероятностей. Гамма-распределение моделирует сумму множества независимых, экспоненциально распределенных переменных. Это можно рассматривать как частный случай экспоненциального распределения.
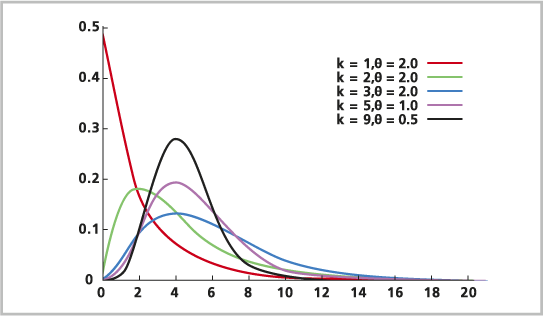
Формула гамма-распределения выглядит следующим образом:
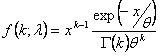
Здесь показан другой способ параметризации гамма-распределения:

При значении альфа, равном 1, гамма-распределение равно экспоненциальному распределению. Когда альфа является целым числом, гамма-распределение становится распределением Эрланга. Для целых значений альфа и бета, равных 2, гамма-распределение становится распределением хи-квадрат с 2 альфа-степенями свободы.
Результирующие переменные больше или равны 0.0. Альфа- и бета-значения должны быть больше 0.0.
Биномиальное распределение
Биномиальное распределение моделирует количество повторений события при наблюдении за последовательностью потенциальных инициаторов события. Например, биномиальное распределение отражает количество людей, умерших от сердечных заболеваний в ходе клинического исследования, количество людей, которые вышли на втором этаже в переполненном лифте, или количество животных в популяции, которые являются носителями определенного генетического признака.
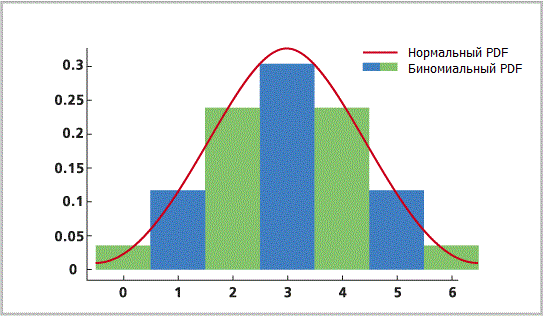
Биномиальное распределение описывает случаи, а не величину. Это может быть модель того, сколько участников финишировало в гонке, а не того, насколько быстрыми они были.
Формула биномиального распределения выглядит следующим образом:
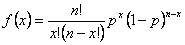
где
n - число наблюдений.
p - вероятность возникновения.
x - количество успешных событий в диапазоне от 0 до n.
Распространенным примером использования биномиального распределения является определение вероятности того, сколько раз выпадет орел при подбрасывании монеты 10 раз (n = 10). Может оказаться 0 орлов из 10, 1 из 10 и так далее; следовательно, x = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. А p - это вероятность для каждого x.
Все попытки являются независимыми, и каждая из них имеет результат успеха или неудачи.
Биномиальное распределение приближается к распределению Пуассона при большом n и малом p. В этом случае, возможно, будет проще использовать распределение Пуассона.
Биномиальное распределение возвращает случайную величину для числа успешных попыток из n, где вероятность успеха в каждом испытании равна p (например, вероятность выпадения орла равна p).
Геометрическое распределение
Геометрическое распределение - это дискретное распределение вероятностей. Существует два основных типа явлений, которые он моделирует: (1) вероятность числа попыток для достижения успеха (например, количество бросков костей, необходимых для выпадения числа 6) или (2) вероятность того, сколько неудач предшествует успеху (например, количество походов, прежде чем вы увидите оленя). Вероятность того, что вы не увидите оленя во время первого похода, равна (1 - p). Во время второго похода вероятность того, что вы не увидите оленя, равна (1 - p) (1 - p). С увеличением количества походов вероятность того, что вы не увидите оленя, экспоненциально уменьшается, и в конце концов один из них будет замечен. Эти события независимы друг от друга.

Формула геометрического распределения выглядит следующим образом:

где
p - вероятность успеха.
n - число попыток.
Геометрическое распределение - это дискретная версия экспоненциального распределения (см. выше). Геометрическое распределение является частным случаем отрицательного биномиального распределения или распределения Паскаля, где r в распределении Паскаля равно 1 (см. ниже).
Отрицательное биномиальное распределение
Отрицательное биномиальное распределение - это дискретное распределение вероятностей. Отрицательное биномиальное распределение основано на испытаниях Бернулли. Испытания Бернулли моделируют события, в которых испытания имеют один из двух исходов (успех или неудача); имеют вероятность успеха p (при этом p одинаково для каждого испытания); и независимы друг от друга. Подбрасывание монеты - это испытание Бернулли. Например, отрицательное биномиальное распределение может моделировать, сколько раз нужно подбрасывать монету, пока не выпадет пять орлов подряд. Таким образом, отрицательное биномиальное распределение моделирует количество неудач, предшествующих успеху. Когда r является целым числом, отрицательный биномиал становится частным случаем, известным как распределение Паскаля.
Формула отрицательного биномиального распределения выглядит следующим образом:
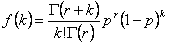
где
r - количество неудач.
p - вероятность успеха.
k - количество успешных событий в диапазоне от 0 до n.
Когда отрицательное биномиальное распределение соответствует подбрасыванию монеты, возвращается случайное значение, показывающее количество выпадений орла.