Доступно с лицензией Spatial Analyst.
Инструмент Статистика набора каналов предоставляет статистику для многомерного анализа набора каналов растра. При использовании опции Вычислить ковариационную и корреляционную матрицу, помимо основных статистических параметров, таких как минимум, максимум, среднее и стандартное отклонение для каждого слоя, в качестве выходных данных будут также получены матрицы ковариации и корреляции. Если включена опция Вычислить гистограмму, статистика гистограммы будет рассчитана и добавлена в выходной файл статистики. Если указана таблица выходной гистограммы, то будет создана таблица выходных данных, содержащая информацию о гистограмме. Если указано название выходной гистограммы, то будут созданы диаграммы гистограммы и добавлены в таблицу содержания.
Матрица ковариации содержит значения дисперсий и ковариаций. Дисперсия – это статистическая мера, показывающая величину отклонений от среднего. Для вычисления дисперсии находится среднее из квадратов разницы между значением ячейки и средним значением для всех ячеек. Дисперсии для каждого слоя могут быть прочитаны по диагонали матрицы ковариации, которая проходит из верхнего левого угла в правый нижний угол матрицы. Дисперсии выражаются как квадрат единиц измерения значений ячеек.
Остальные значения в матрице ковариации – это ковариации между всеми парами входных растров. Для определения ковариации между слоями i и j применяется следующая формула:

, где:
Z – значение ячейки
i, j – слои стека
µ – среднее значение слоя
N – число ячеек
k – обозначает конкретную ячейку
Ковариация двух слоев – это пересечение соответствующей строки и столбца. Ковариация между слоями 2 и 3 – это то же самое, что и ковариация между слоями 3 и 2. Значения матрицы ковариации зависят от единиц измерения значений, в то время как значения матрицы корреляции не зависят от единиц измерения значений.
Матрица корреляции показывает значения коэффициентов корреляции, которые указывают на связь между двумя наборами данных. В случае набора слоев растра, матрица корреляции отражает связь значений ячеек с одного слоя растра со значениями ячеек на другом слое растра. Корреляция между двумя слоями – это мера зависимости между слоями. Это ковариация между двумя слоями, деленная на произведение их стандартных отклонений. Поскольку это отношение, его значение является безразмерным. Уравнение для вычисления корреляции следующее:

Коэффициенты корреляции находятся в диапазоне от +1 до -1. Положительная корреляция указывает на прямую связь между двумя слоями, то есть когда значения ячеек на одном слое увеличиваются, скорее всего, будут увеличиваться и значения ячеек на другом слое. Отрицательная корреляция означает, что переменная меняется по отношению к другой переменной противоположным образом. Нулевой коэффициент корреляции означает, что два слоя независимы друг от друга.
Матрица корреляции симметрична. Ее значения по диагонали из верхнего левого угла в нижний правый угол равны 1.0000, поскольку коэффициент корреляции для идентичных слоев равен +1.
Примеры Выходного файла статистики
Выходной файл статистики поддерживает два выходных формата: формат значений, разделенных запятыми (CSV), или формат Markdown. Ниже приведены примеры выходных файлов статистики этих форматов для четырехканального входного растра.
Выходной CSV
Когда выходной файл статистики указан как текстовый файл (с расширением .txt, .csv или .asc), он будет сохранен в формате значений, разделенных запятыми (CSV), что позволит импортировать его в другое ПО (например, Excel) для дальнейшего анализа или визуализации.
Ниже приведено содержимое текстового файла, созданного с отключенными опциями Вычислить ковариационную и корреляционную матрицу и Вычислить гистограмму. Пути к исходным данным для входных слоев указаны в верхней части файла.
Output Band Collection Statistics Input Layers Layer,Path Layer_1,C:\example\mb_data.tif\Band_1 Layer_2,C:\example\mb_data.tif\Band_2 Layer_3,C:\example\mb_data.tif\Band_3 Layer_4,C:\example\mb_data.tif\Band_4 Statistics of Individual Layers Layer,Min,Max,Mean,Std. Dev. 1,48.00000,255.00000,73.70110,11.90945 2,22.00000,255.00000,33.73108,7.49241 3,17.00000,255.00000,31.77404,11.40892 4,13.00000,255.00000,82.51136,17.67144
Выходные данные Markdown
Выходной файл статистики будет сохранен в формате Markdown, если расширение файла указано как .md.
Ниже приведено содержимое файла Markdown, созданного с включенной опцией Вычислить ковариационную и корреляционную матрицу и отключенной опцией Вычислить гистограмму, при просмотре в виде обычного текстового файла.
# Output Band Collection Statistics ### Input Layers | Layer | Path | | ------: | ----------------------------: | | Layer_1 | C:\example\mb_data.tif\Band_1 | | Layer_2 | C:\example\mb_data.tif\Band_2 | | Layer_3 | C:\example\mb_data.tif\Band_3 | | Layer_4 | C:\example\mb_data.tif\Band_4 | ### Statistics of Individual Layers | Layer | Min | Max | Mean | Std. Dev. | | ----: | -------: | --------: | -------: | --------: | | 1 | 48.00000 | 255.00000 | 73.70110 | 11.90945 | | 2 | 22.00000 | 255.00000 | 33.73108 | 7.49241 | | 3 | 17.00000 | 255.00000 | 31.77404 | 11.40892 | | 4 | 13.00000 | 255.00000 | 82.51136 | 17.67144 | ### Covariance Matrix | Layer | 1 | 2 | 3 | 4 | | ----: | --------: | --------: | --------: | --------: | | 1 | 141.83498 | 86.72548 | 131.13040 | -54.33298 | | 2 | 86.72548 | 56.13628 | 84.01048 | -24.88371 | | 3 | 131.13040 | 84.01048 | 130.16340 | -53.35075 | | 4 | -54.33298 | -24.88371 | -53.35075 | 312.27971 | ### Correlation Matrix | Layer | 1 | 2 | 3 | 4 | | ----: | -------: | -------: | -------: | -------: | | 1 | 1.00000 | 0.97193 | 0.96509 | -0.25817 | | 2 | 0.97193 | 1.00000 | 0.98280 | -0.18794 | | 3 | 0.96509 | 0.98280 | 1.00000 | -0.26462 | | 4 | -0.25817 | -0.18794 | -0.26462 | 1.00000 |
Выходные данные Markdown после построения изображения
Ниже приведен пример того, как выглядит выходной файл в формате Markdown после построения изображения. Этот выходной файл создается с включенной опцией Вычислить гистограмму и отключенной опцией Вычислить ковариационную и корреляционную матрицу.
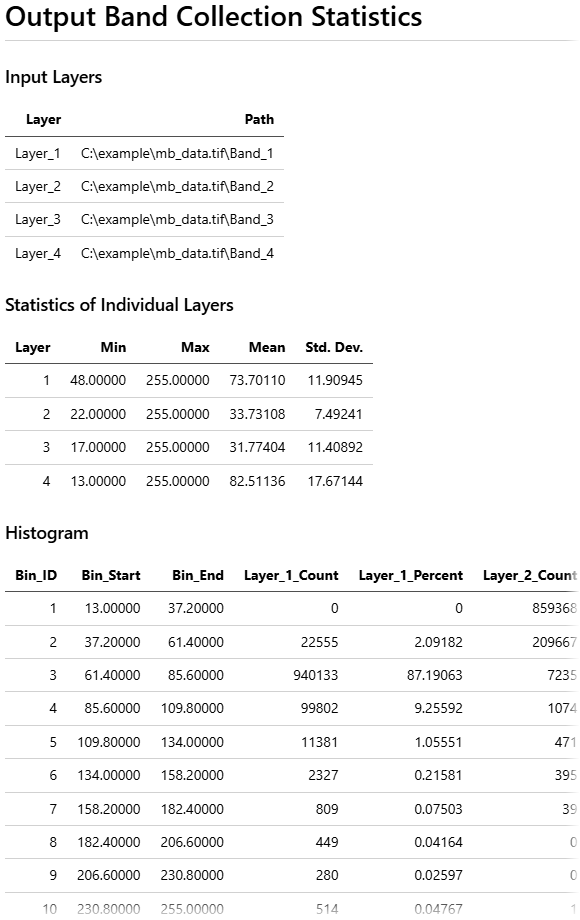
Дополнительные ресурсы
Дополнительную информацию см. здесь:
Snedecor, G. W., and W. G. Cochran. 1968. Statistical Methods, 6th ed. Ames, Iowa: The Iowa State University Press.