需要 Geostatistical Analyst 许可。
模拟概念
模拟在广义上是指使用模型复制现实的过程。在地统计中,模拟是随机函数(表面)的实现,其与生成该模拟的样本数据拥有相同的地统计要素(使用均值、方差和半变异函数来度量)。更具体地说,高斯地统计模拟 (GGS) 适用于连续数据,并假设数据或数据的变换具有正态(高斯)分布。GGS 所依托的主要假设是数据是静态的 - 均值、方差和空间结构(半变异函数)在数据空间域上不发生改变。GGS 的另一个主要假设是建模的随机函数为多元高斯随机函数。
同克里金法相比,GGS 具有优势。由于克里金法是基于数据的局部平均值的,因此,其可生成平滑的输出。另一方面,GGS 生成的局部变异性的制图表达比较好,因为 GGS 将克里金法中丢失的局部变异性重新添加到了其生成的表面中。对于由 GGS 实现添加到特定位置的预测值中的变异性,其平均值为零,这样,很多 GGS 实现的平均值会趋向于克里金预测。下图对此概念进行了说明。各种实现以一组堆叠输出图层的形式表示出来,并且特定坐标位置的值服从高斯分布,其平均值等于该位置的克里金估计值,而扩散程度则由该位置上的克里金法方差给出。
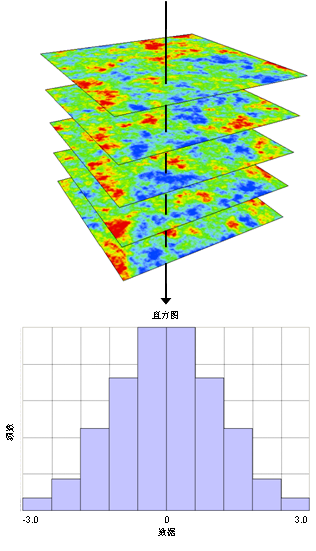
提取值到表工具可以用来为上图中的图形生成数据,在对 GGS 生成的输出进行后处理时该工具也很有用。
对 GGS 的使用在地统计实际操作中日益呈现出一种趋势,它不是追求获得每个未采样位置的最佳无偏预测结果(正如克里金法所体现的),而是强调对决策分析和风险分析的不确定性的特证描述,这样更适合于呈现数据中的全局趋势 (Deutsch and Journel 1998, Goovaerts 1997)。模拟还会克服克里金估计值中的条件偏差带来的问题(高值区域预测值通常偏低,而低值区域预测值通常偏高)。
对于所研究属性的空间分布,地统计模拟可为其生成多个具有同等可能性的制图表达。可基于这些制图表达来测量未采样位置的不确定性,这些未采样位置在空间上被一起选取,而不是逐个被选取(如同通过克里金法方差进行测量一样)。此外,克里金法方差通常独立于数据值,且通常不能用作估计精度的测量值。另一方面,可以通过使用多个模拟实现(该实现用呈正态分布的输入数据通过简单克里金模型进行构建,即,数据呈正态分布或已使用常态得分变换或其他类型的变换对数据进行了变换)为未采样位置的估计值构建分布来测量估计精度。对于使用估计数据值的风险评估和决策分析而言,这些不确定性的分布很关键。
GGS 假设数据呈正态分布,但在实际中,很少会出现这种情况。对数据执行常态得分变换,使得数据符合标准正态分布(均值 = 0,方差 = 1)。然后对此正态分布数据进行模拟,并对结果做反向变换,以便以原始单位获得模拟输出。对正态分布数据使用简单克里金法时,该克里金法所提供的克里金估计值和方差可完全定义研究区域中每个位置的条件分布。这样,您可以在只知道每个位置的这两个参数的情况下绘制随机函数(未知采样表面)的模拟实现,这也是 GGS 基于简单克里金模型和正态分布数据的原因。
“高斯地统计模拟”工具支持两种类型的模拟:
- 条件模拟遵循数据值(除非克里金模型中包含测量误差)。由于模拟会在格网像元中心生成值,因此,如果此值与采样点的位置不完全对应,则采样位置的测量值与模拟值可能会不同。条件模拟也将以平均方式(即,在很多实现上平均)复制数据的均值、方差和半变异函数。模拟表面看起来很像克里金预测地图,但其将显示更多的空间变异性。
- 非条件模拟不遵循数据值,但会以平均方式复制数据的均值、方差和半变异函数。模拟表面所显示的空间结构类似于克里金地图,但输入数据中存在高值或低值的地方不一定会出现高值和低值。
模拟示例
示例 1
在世界上的许多城市和地区,空气质量都是令人关注的重要健康指标之一。在美国,众所周知,洛杉矶的空气质量不是很好,分布密集的监控网络每半天就对臭氧、微粒物质和其他污染物等数据进行一次收集。基于此空气质量数据,可获得每种污染物的浓度以及污染物每年超过州空气质量标准和联邦空气质量标准的天数 (http://www.arb.ca.gov/html/ds.htm)。由于这两个测量值均支持对在某个特定区域内生活进行感染风险的局部评估,因此,每年超过临界阈值的天数可用来建立显示超过阈值概率的内插地图。
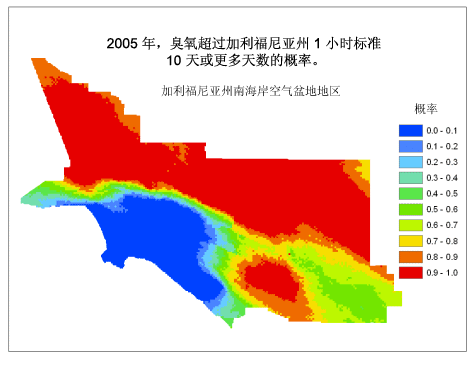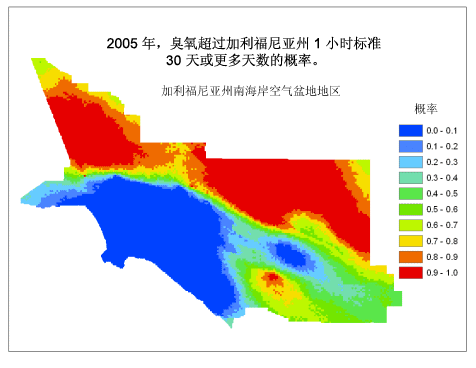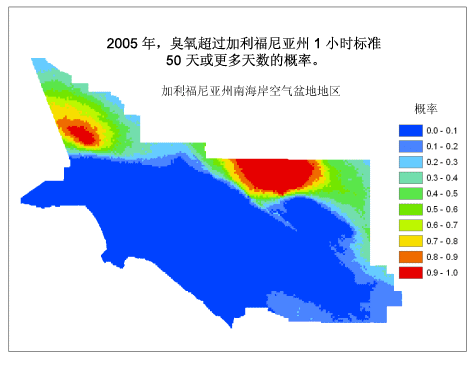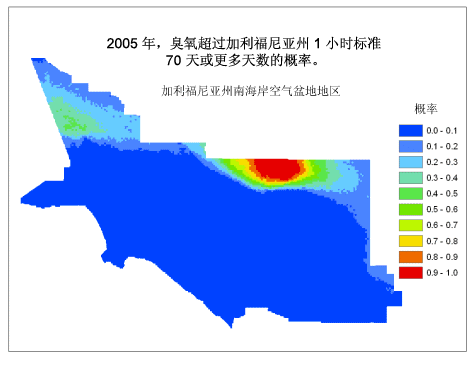
在本示例中,对 2005 年加利福尼亚州每个监测站臭氧超过阈值的天数做了调查,并通过拟合该数据创建了一个半变异函数。并使用条件模拟生成了多个实现。每个实现都是一个地图,用于表示 2005 年污染物超过阈值的天数。然后对这些实现进行后处理,以估计污染物每年超过州阈值的天数多于 10 天、20 天、30 天、40 天、50 天、60 天和 70 天的概率(所有监测站记录的超过阈值的最大天数为 80 天)。下面的动画显示了生成的南海岸空气盆地地区(其中包括洛杉矶和内陆城市)的臭氧地图。海岸附近的空气质量明显好于内陆地区,主要是因为在这一地区,风向主要是由西向东吹。
这类地图可用于确定污染减轻策略的优先级,通过解答诸如“我可以忍受多少污染?”、“生活在某一特定区域我需要忍受多少污染?”等问题, 来研究健康与环境质量之间的关系并帮助人们确定适宜居住的地点。
示例 2
在很多应用中,都使用与空间相关的变量作为模型的输入(例如,石油工程中的流动模拟)。在此类情况中,模型结果的不确定性是通过以下过程生成大量模拟来进行评估的:
- 1. 为变量模拟大量具有同等可能性的实现。
- 2. 使用模拟变量作为输入来运行模型(通常称为传输函数)。
- 3. 汇总模型运行以评估模型输出的变异性。
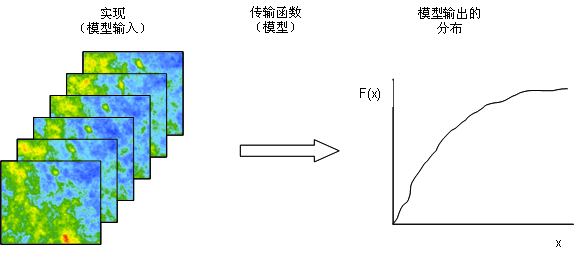
输出的统计数据可用来测量模型的不确定性。
上述过程的一个实际示例是:为在新墨西哥州东南部成立一个废品隔离试验工场 (WIPP) 作为超铀废物的存储设施而进行的研究 (https://www.wipp.energy.gov/)。
科学家曾对位于地表以下 2000 多英尺的盐矿床进行了评估,以便将其用作废料的潜在存储设施。然而,矿床刚好位于蓄水层之上,因此,担心地下水可能会传输站点泄露的废弃物。为了证明 WIPP 的安全性,科学家不得不说服美国 环境保护局:流经蓄水层中的地下水流速非常之低,污染周围环境的可能性微乎其微。
导水系数值决定了蓄水层中的水流流速,并针对拟建的 WIPP 站点附近蓄水层获得了多个此类值。使用以数字方式求解的水文方程为地下水流建模,该方程需要导水系数值,该值在常规格网上进行预测。如果使用了导水系数的克里金估计值,则导水系数值将基于邻近导水系数值的(加权)平均值,而已建模的地下水的流动时间将只会基于这些平均值。由于克里金法将生成平滑地图,所以插值表面会缺少导水系数值极高或极低的区域。要正确地对风险进行分析,科学家必须考虑可能出现的最坏情况,因此需要生成流动时间值的整个概率分布。通过此分布,科学家将能够使用地下水流动时间分布的较低尾值(对应极高流速),而不是平均流动时间,来评估 WIPP 的适宜性。曾使用条件模拟来生成流动时间值的概率分布。
废品通过地下水进行传输的概率只是评估 WIPP 适宜性时考虑的众多危及人类健康情形中的一种。复杂风险分析在评估 WIPP 是否适宜进行核废料处理以及使公众和政府监管部门确信其适宜性方面起了很大作用。在长达 20 多年的时间里,在进行了大量的科学研究、公众意见收集以及进行了大量监管工作之后,WIPP 最终于 1999 年 3 月 26 日开始运作。
应该生成多少实现?
模拟研究的结果不应取决于所生成实现的数量。确定生成多少实现的其中一种方法是:在一小部分数据属性域中对比不同实现数的统计数据(使用子集以节省时间)。随着实现数量的增加,统计数据将趋向于一个固定值。下面的示例中检查的统计数据是第一个分位数和第三个分位数,它们是为美国斯威康星州的一小部分(子集)模拟高程表面(在海平面以上,以英尺为单位)而计算的值。
上方的图显示的是前 100 个实现的高程波动。下方的图显示的是 1000 个实现的结果。
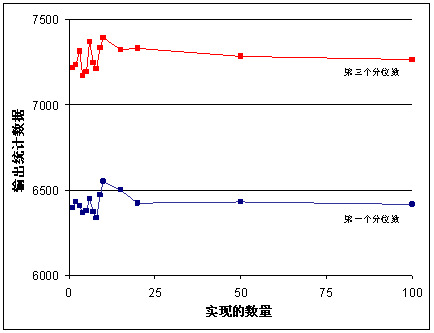
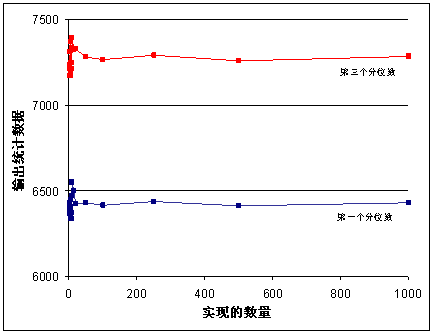
在本例中,值在大约 20 个模拟之后稳定下来。在很多情况下,至少需要运行 100 个实现才能确定超出阈值的均值和概率所需的足够信息。如果使用数量更多的实现,则可为汇总统计数据和模型输出变量提供更高程度的确定性,但所需计算时间也更长。
要了解有关如何在 ArcGIS 中实现高斯地统计模拟的详细信息,请参阅帮助部分高斯地统计模拟的工作原理。
参考文献
Deutsch, C.V., and A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide. 2nd Ed. Oxford University Press, New York, pages 119–122.
Goovaerts, P. 1997. Geostatistics for Natural Resource Evaluation. Oxford University Press, New York, pages 369–376.