需要 Geostatistical Analyst 许可。
实现的生成方法
使用“高斯地统计模拟”时,首先要创建一个基于标准正态分布(平均值 = 0 且 方差 = 1)绘制的随机分配值的格网。然后,将协方差模型(基于在需要作为模拟的输入的简单克里金图层中指定的半变异函数)应用到栅格。这样可以确保栅格值遵循输入数据集中的空间结构。生成的栅格构成一个非条件实现,而且通过每次使用不同的包含正态分布值的栅格可生成更多的非条件实现。有关该方法的详细信息,请参阅 Dietrich and Newsam (1993)。
如果已选择条件模拟,则会通过克里金法将非条件栅格条件化。该过程利用每个位置处的克里金估计值(预测值)确保模拟值遵循输入数据值,且通常情况下,克里金预测值是复制的。有关使用克里金法条件化实现的详细信息,请参阅 Journel (1974)。
不过,如果简单克里金模型包含测量误差,则不会遵循输入数据值(在简单克里金图层或者模拟的实现里)。除此之外,“高斯地统计模拟”工具还能够使用连续的(或平滑的)搜索邻域,这样可以避免因克里金法中使用的局部邻域的变化而导致模拟表面中出现不连续。有关详细信息,请参阅 Aldworth (1998) 和 Gribov and Krivoruchko (2004)。
要了解有关地统计模拟概念的详细信息以及条件模拟和非条件模拟的示例,请参阅关于地统计模拟的重要概念的帮助。
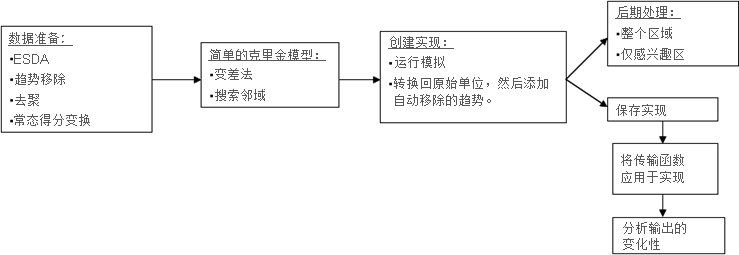
高斯地统计模拟的一般工作流包括:准备数据、创建实现、在后台将结果传输到原始单元中,以及后处理结果和/或将结果用作传输函数(模型)的输入以评估模型输出中的变异性。该过程如下图所示:
检查模拟输出
应检查实现以确认如下内容:
- 输出值、输出值的空间模式以及位置都是合理的。
- 平均来看,模拟数据的直方图可再现输入数据的直方图。
- 平均来看,模拟数据的半变异函数可再现输入数据的半变异函数。
- 对于条件模拟,能够遵循输入数据值(除非简单克里金模型包含测量误差)。
后处理
生成实现以后,通常会对实现进行后处理,以获得汇总结果。“高斯地统计模拟”工具允许使用多种后处理选项,它们可以在各栅格的整个空间范围或在特定的感兴趣区内执行。这些区域通过在该工具的“输入统计面”选项中指定面要素类来定义。在这两种情况下的输出是相似的:后处理整个栅格会生成汇总栅格,而后处理面区域会生成一个包含各面的汇总统计数据的面输出要素类。
后处理整个栅格范围
- 输出栅格包含为各位置(像元)生成的最小值、最大值、平均值、标准差、第一四分位数、中值(第二四分位数)和第三四分位数。此外,还可指定将根据各像元模拟值的分布方式返回与自身对应的值的分位数。还可指定阈值,该值将返回超出各像元阈值的模拟值所占的百分比。
- 请注意,可通过指定边界多边形或一组点来限制要进行后处理的范围(在本例中,生成了一个凸包并将它用作边界多边形)。值仅会在边界多边形内进行模拟。
感兴趣区域的后处理
- 当指定了感兴趣面区域时,各面的输出会自动包含下表中描述的汇总统计数据。此外,还可指定分位数值和阈值(后处理整个栅格范围时)。表中还描述了在选中这些选项的情况下生成的输出。
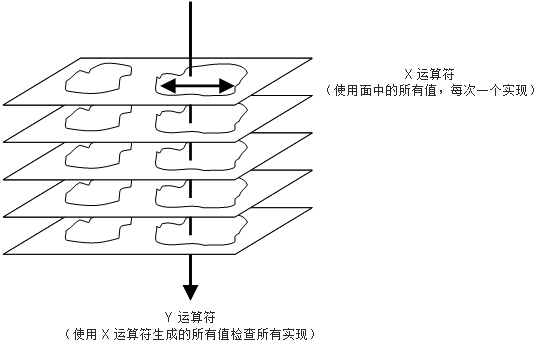
- 这些面的汇总输出使用如下图中所示的运算符计算得到。X 运算符利用面内的所有值并为每个实现计算出一个值。Y 运算符使用所有实现中的值。Y 运算符的输入是各实现的面区域的值(由 X 运算符计算得出)。
下表列出了输出要素类中字段的含义。
| 字段名 | 说明 |
|---|---|
MIN | 面内所有实现中任意像元的最小值。 |
MAX | 面内所有实现中任意像元的最大值。 |
MEAN | 面内所有实现中全部像元的平均值。 |
STDDEV | 面内所有实现中全部像元的标准差。 |
QUARTILE1 | 面内所有实现中全部像元的第一四分位数值。 |
MEDIAN | 面内所有实现中全部像元的中值。 |
QUARTILE3 | 面内所有实现中全部像元的第三四分位数值。 |
QUANTILE | 面内所有实现中与全部像元的用户指定分位数对应的值。 |
P_THRSHLD | 在面内所有实现的全部像元中,超出用户指定阈值的像元所占的百分比。 |
X_Y | X 函数应用于面内各像元的值,每次一个实现。该过程相当于运行“分区统计”工具,该工具将面作为区域,每次将一个实现作为值格网。Y 函数应用于由 X 函数生成的值。
|
CELL_COUNT | 面内的像元数量。如果像元中心位于面内,就认为该像元位于面内。负计数表示面的一部分位于模拟栅格范围以外和/或裁剪边界以外。负数本身表示面内的像元总数。 |
SOURCE_ID | 输入面要素类的对象或要素 ID。 |
对于边界多边形和感兴趣区域面选项,如果像元中心位于面的边界内,就会认为该栅格像元位于面内。
条件模拟和后处理输出示例
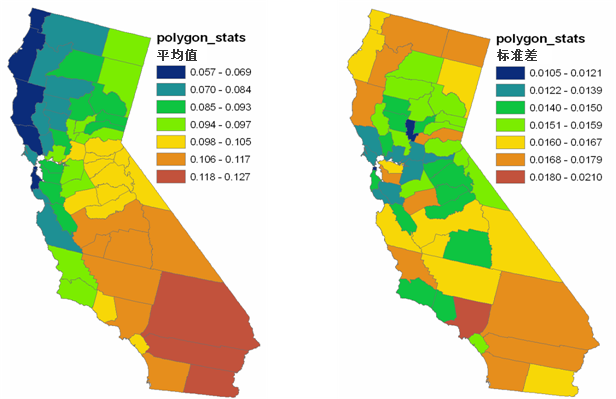
下图显示出通过对输出进行面后处理得到的条件模拟结果。这些地图显示出加利福尼亚州各县臭氧值的 100 个实现的平均值和标准差。可对这些平均值和标准差进行利用,例如用于疾病的发生需要与各县的平均臭氧值进行比较的流行病学研究中。
参考材料和更多阅读材料
Aldworth, J. 1998. Spatial Prediction, Spatial Sampling, and Measurement Error. Ph.D. Thesis, Iowa State University. 186.
Chiles, J. P., and P. Delfiner. 1999. Geostatistics: Modeling Spatial Uncertainty. New York: John Wiley & Sons, 449–471.
Deutsch, C. V., and A. G. Journel. 1998. GSLIB Geostatistical Software Library and User's Guide, 2nd edition. New York: Oxford University Press, 119–141.
Dietrich, C. R., and G. N. Newsam. 1993. "A Fast and Exact Method for Multidimensional Gaussian Stochastic Simulations." Water Resources Research 29 (8): 2861–2869.
Goodchild, M. F., B. O. Parks, and L. T. Steyaert. 1993. Environmental Modeling with GIS. New York: Oxford University Press, 432-437.
Gribov, A., and K. Krivoruchko. 2004. "Geostatistical Mapping with Continuous Moving Neighborhood." Mathematical Geology 36 (2): 267–281.
Journel, A. G. 1974. "Geostatistics for Conditional Simulation of Ore Bodies." Economic Geology 69: 673–687.
Leuangthong, O., J. A. McLennan, and C. V. Deutsch. 2004. "Minimum Acceptance Criteria for Geostatistical Realizations." Natural Resources Research 13 (3): 131–141.