核插值是一阶局部多项式插值法的一个变型,此方法使用一种类似于在用于估算回归系数的岭回归中使用的方法来防止在计算过程中出现不稳定性。当评估值仅存在较小偏差且比无偏差评估值更加精确时,可以将其作为首选评估值。例如,可以在 Hoerl and Kennard (1970) 中了解到岭回归方面的详细信息。
“局部多项式插值法”预测误差是在假设模型正确(即,每个位置的空间条件数都非常小)的条件下估计的。此假设经常被违反,并且预测和预测标准误差不稳定的区域空间条件数会高亮显示。在“核平滑”模型中,通过使用山脊参数将少量偏差引入方程解决了非常大的预测标准误差和可疑的预测的问题。这使得空间条件数的地图毫无必要。因此,“核插值法”仅为输出表面类型提供“预测”和“预测标准误差”。由于为了稳定预测山脊参数而引入了偏差,因此在仍然能够维持模型稳定性的情况下山脊参数应尽可能的小。此过程的详细信息可以参考《存在障碍的数据趋势和插值法的局部多项式》,Gribov 和 Krivoruchko(2010 年)。
两个模型之间的另一个区别在于,核插值模型使用两点间的最短距离,因此,位于指定的不透明(绝对)障碍的侧面上的点会通过一系列直线相连。
核插值法使用以下径向对称核:指数、高斯、四次式、Epanechnikov、5 阶多项式和常数。核的带宽由观测值周围的矩形确定。
当使用一阶多项式时,Epanechnikov 核通常会生成比较理想的结果。不过,根据数据,交叉验证和验证诊断可能会建议使用另一种核,Fan and Gijbels (1996)。
下面对具有绝对障碍的含障碍的核插值法预测(左侧)和不具有绝对障碍的含障碍的核插值法预测(右侧)进行比较。请注意,左侧图像障碍处的等值线突然变化,而右侧图像障碍处的等值线十分平滑。
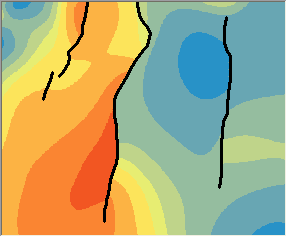
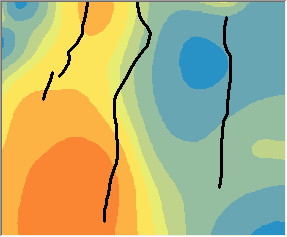
在水文和气象应用中,可优先采用基于两点间最短距离的模型。
核函数
核函数:对于以下所有公式,r 是中心在点 s 的半径,h 是带宽。
- 指数:
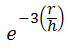
- 高斯:
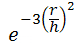
- 四次式:
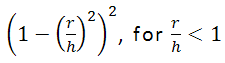
- Epanechnikov:
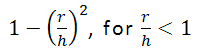
- 5 阶多项式:
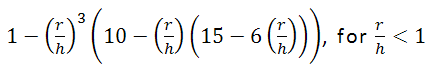
- 常量:
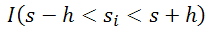
其中 I(表达式) 是一个指示函数,如果表达式为真,则使用值 1;如果表达式为假,则使用值 0。
带宽参数适用于“常量”函数以外的所有核函数。指数、高斯、和常量核函数还支持平滑搜索邻域以便减少核的范围。
参考材料和更多阅读材料
Fan, J. and Gijbels, I. (1996).Local Polynomial Modelling and Its Applications, Chapman & Hall.London.
Hoerl, A.E. and Kennard, R.W. (1970), Ridge regression:biased estimation for nonorthogonal problems, Technometrics, 12, 55-67.
Yan, Xin.(2009) Linear regression analysis :theory and computing.Published by World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck Link, Singapore 596224.