空间约束多元聚类工作原理

当我们观察周围的世界时，我们会很自然地对所看到的事物进行组织、分组、区别和划分，以便帮助我们更好地了解周围的一切；这类心理分类过程是学习和理解的基础。同样，为了帮助您了解以及更好地理解数据，您可以使用空间约束多元聚类工具。给定要创建的聚类数，它将寻找一个能够使每个聚类中的所有要素都尽可能相似但各个聚类之间尽可能不同的解。要素相似性是基于您为分析字段参数指定的一组特性，同时还可以包括对于聚类大小的约束。此工具使用的算法采用连通图（最小跨度树）和一种被称为 SKATER 的方法来查找数据中存在的自然聚类以及证据累积以评估聚类从属度似然法。

提示：

聚类、分组和分类技术是机器学习中使用最广泛的一些方法。空间约束多元聚类工具使用非监督的机器学习方法来确定数据中的自然聚类。由于这些分类方法不需要一组预先分类的要素来指导或进行训练以确定数据的聚类，因此可将其视为非监督类型。

虽然存在数百个类似这样的聚类分析算法，但它们都被归类为 NP-hard 问题。这意味着要确保某个解能够完美地实现组内相似性和聚类间差异最大化，唯一方法就是对要聚类的要素的每一种可能组合都进行尝试。虽然这对于少量的要素是可行的，但对于问题来说，会很快变得非常棘手。

不但确保找到最佳解非常困难，而且尝试找到一种最适合所有可能数据情景的聚类算法也不现实。各个聚类包含的形状、大小和密度各不相同；属性数据可能包括各种范围、对称性、连续性和测量单位。这就是过去 50 年来开发了如此众多不同聚类分析算法的原因。因此，将空间约束多元聚类视为一种可帮助您更好地了解数据基本结构的探索性工具比较合适。

潜在的应用

应用此工具的一些方法如下：

• 如果您收集了有关动物观察方面的数据，以便更好地了解它们的领地，空间约束多元聚类工具可能很有帮助。例如，了解鲑鱼在不同生命阶段的聚集地点和时间，可以帮助您规划保护区，以帮助确保成功繁育。
• 作为一名农学家，您可能想将研究领域内的不同土壤进行分类。对通过一系列样本发现的土壤特征使用空间约束多元聚类可以帮助识别出明显的、空间上相邻的土壤类型的聚类。
• 按购买方式、人口统计特征和旅行方式对客户进行聚类，可以帮助您为公司产品制订有效的营销策略。
• 城市规则师常常需要将各个城市划分成不同的邻域，以便有效地定位公共设施、促进地方能动性并提高社区参与度。对城市街区的物理和人口统计特征使用空间约束多元聚类，可以帮助规划师确定具有相似物理和人口统计特征并且在空间上相邻的城市区域。
• 每当对聚合的数据进行分析时，生态谬误都是一个众所周知的统计推断问题。通常，用于分析的聚合方案对您想要分析的内容没有任何关系。例如，人口普查数据是根据人口分布而聚合，而人口分布情况可能不是用来进行火灾分析的最佳选择。针对与目前分析问题准确相关的一组属性，将可能的最小聚合单位划分成同质区域，是降低聚合偏差和避免生态谬误的一种有效方法。

输入

此工具将具有点或面输入要素、输出要素的路径、一个或多个分析字段、表示所要创建的聚类数的整数值以及应在聚类算法中应用的空间约束类型。另外，还有许多可选的参数，可用于针对每个聚类要素数量的最大值或最小值，或每个聚类属性值总和的最大值或最小值设置聚类大小约束。以及一个最佳聚类数评估输出表。

分析字段

选择反映比率、间隔或序数测量系统的数值字段。虽然标称数据可以使用“哑元”（二进制）变量进行表示，但它们通常不像其他数值变量类型一样起作用。例如，您可以创建一个名为 Rural 的变量，并向每个要素（如每个人口普查区）分配 1（如果大部分是乡村）和 0（如果大部分是城市）。但是，如果要与空间约束多元聚类结合使用，那么此变量更好的表示方法是，使用与每个要素相关的乡村面积的数量或比例来表示。

注：

由于方差较大的变量（其中数据值围绕平均值扩散）对聚类的影响大于方差较小的变量对聚类的影响，因此分析字段中的值将由工具进行标准化。属性值的标准化涉及 Z 变换，即从每个值中减去所有值的平均值然后除以所有值的标准差。标准化将所有属性放在同一比例中，即使它们由不同类型的数字表示时也是如此：比率（0 到 1.0 的数字）、人口（超过 1 百万）和距离（例如，千米）。

您应该选择您认为可以将一聚类要素与另一聚类要素区别开来的变量。例如，假设您想要按学生在标准化成绩测试中的成绩对学区进行聚类。您可以选择各种分析字段，如整体测试得分、数学和阅读等特定科目的成绩、满足一些最低考试得分阈值的学生比例等。运行空间约束多元聚类工具时，将为每个变量计算 R² 值，并在消息窗口中进行报告。例如，在下面的汇总中，根据学生测试得分、该地区未上完中学的成人比例、每个学生的开支以及学生与教师的平均比率，来对学区进行聚类。请注意，TestScores 变量具有最高的 R² 值。这表明此变量能够最有效地将学区聚类。R² 值反映在聚类流程之后原始 TestScores 数据中的变化的保留程度，因此，特定变量的 R² 值越大，变量越能更好地对要素进行区分。

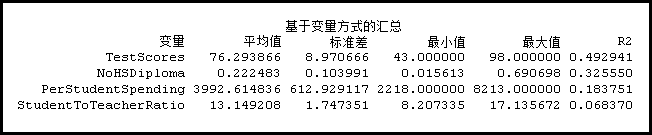
抢先版本：

R² 的计算公式如下：

(TSS - ESS) / TSS

其中 TSS 是总平方和，ESS 是回归平方和。TSS 的计算方法是先计算平方，然后再计算变量全局平均值偏差的总和。ESS 的计算方法相同，不同之处在于偏差是分组计算：从所属组的平均值减去每个值，然后再计算平方和总和。

聚类大小约束

可通过聚类大小约束参数管理聚类的大小。您可以设置每个聚类必须满足的最大或最小阈值。大小约束可以是每个聚类所包含的要素数量，也可以是属性值的总和。例如，如果根据一组经济变量对美国各县进行聚类，则可以指定每个聚类的最小人口数为 500 万，最大人口数为 2500 万。或者，可指定每个聚类都必须至少包含 30 个县。

在指定每个聚类的最大值约束时，该算法将以单个聚类开始，并对空间上相邻和具有相似值的聚类进行分割。考虑到每次分割时的所有变量，将会创建新聚类，直到所有聚类大小都低于每个聚类的最大值。

SKATER 通过对感兴趣要素具有相似值的数据进行空间分区来形成聚类。聚类大小约束参数可能不会对所有聚类生效。如果定义的聚类大小约束不支持最佳聚类定义就会出现这种情况。

SKATER 还可通过对所有指定分析字段具有相似值的数据进行空间分区来形成聚类。聚类大小约束可能不会对所有聚类生效。如果最大约束和最小约束的设置值彼此相近可能会发生这种情况，基于空间约束构建最小跨度树也可能会引起这种情况的发生。如果发生了这种情况，该工具将完成工作，没有满足特定要求的聚类将在消息窗口中予以报告。

聚类数

有时，您会知道最适合于您的问题的聚类数。例如，如果您有五位销售经理，并且要为每一位经理指定自己的相邻区域，那么您可以为聚类数参数使用 5。但是，在许多情况下，对于选择具体聚类数您没有任何标准；而只是希望得到一个数，这个数能够最恰当地对要素相似性和差异性进行区分。为帮助您解决这种情形，您可以留空聚类数参数，然后让空间约束多元聚类工具评估将要素分为 2、3、4 和多达 30 个聚类时的有效性。聚类有效性通过 Calinski-Harabasz 伪 F 统计量来测量，它是一个反映聚类间方差和聚类内方差的比率。换言之，是反映组内相似性和组间差异的比率，如下所示：

假设您想要创建四个空间上相邻的聚类。在这种情况下，此工具将创建一个既能反映要素的空间结构又能反映其相关的分析字段值的最小跨度树。然后，将使用此工具确定切割树的最佳位置，以便创建两个单独的聚类。接下来，此工具将决定对生成的两个聚类中的哪个聚类进行划分，以生成三个最佳的聚类解决方案。将划分两个聚类中的其中一个，另一个聚类则保持不变。最后，此工具将决定应对生成的三个聚类中的哪个聚类进行划分，以提供最佳的四个聚类解决方案。对于每个分组，最佳解决方案即为将聚类内相似性和聚类差异性最大化的解决方案。当聚类中所有要素的分析字段值相同时，将不再对该聚类进行划分（随机性除外）。如果生成的所有聚类中具有的要素均相同，那么即使没达到您所指定的聚类数值，空间约束多元聚类工具也将停止创建新聚类。当所有分析字段具有相同值时，不存在任何划聚类的依据。

空间约束

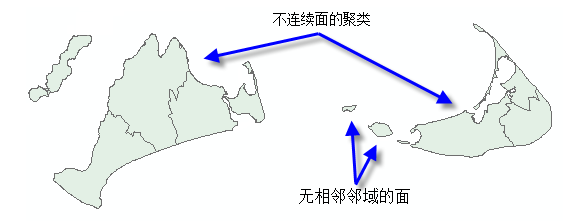
空间约束参数可以确保生成的聚类在空间上相邻。可以启用面要素类的邻接选项，来指明仅当要素与聚类中的另一从属度共享某条边（仅邻接边）或共享某条边或某个折点（邻接边拐角）时，才表示这些要素属于同一聚类。但是，如果数据集包括不连续面或根本没有相邻邻域的面的聚类，则面邻接选项并不是很好的选择。

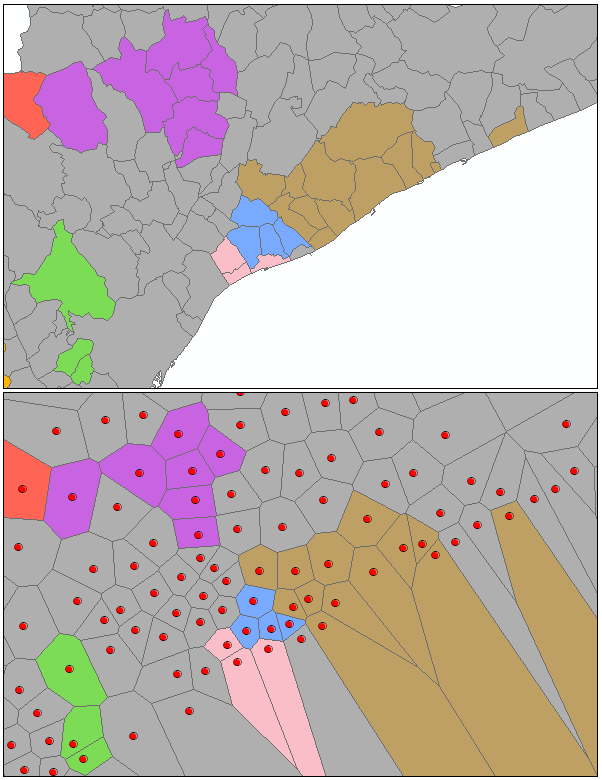
修剪型 Delaunay 三角测量选项适合点或面要素，并确保仅当某个要素至少有一个其他聚类从属度是自然邻域 (Delaunay Triangulation) 时，该要素才能包括在聚类中。从概念上讲，Delaunay 三角测量可以根据要素质心创建不重叠的三角网。每个要素是一个三角形结点，具有公共边的结点被视为邻域。然后将这些三角形剪裁成凸包，以确保要素无法与凸包外的任何要素相邻。此选项不得用于具有重合要素的数据集。另外，由于 Delaunay 三角测量方法会将要素转换为泰森面来确定邻域关系，特别是与面要素的邻域关系，有时是与数据集中外围要素的邻域关系，因此使用此选项所得的结果可能不会始终与您的预期相符。请注意，在下图中，某些分组的原始面不是连续的。然而，当它们转换为泰森多边形时，所有分组的要素实际上都共享边。

对于修剪型 Delaunay 三角测量，泰森面邻接定义了邻域关系。

如果想让生成的聚类在空间和时态上都邻近，可使用生成空间权重矩阵工具创建空间权重矩阵文件 (SWM)，然后为空间关系的概念化参数选择空间时间窗。然后，可以在运行空间约束多元聚类工具时，为权重矩阵文件参数指定您使用生成空间权重矩阵工具创建的 SWM 文件。

注：

虽然要素之间的空间关系存储在 SWM 文件中，并由空间约束多元聚类工具用于施加空间约束，但在分组过程中并不涉及实际的权重。SWM 文件只用于跟踪同一个聚类中可以包含哪些要素以及不可以包含哪些要素。

最小跨度树

为将聚类从属度限制为相连或相邻要素，工具首先会构造一个表示要素间邻域关系的连通图。连通图上的最小跨度树将汇总要素空间关系和要素数据相似性。要素将成为最小跨度树中通过权重边进行连接的节点。每个边的权重与其连接的对象的相似性成正比。构建最小跨度树后，树中的分支（边）将被剪除，从而生成两个最小跨度树。要剪除的边会被选择，以使生成的聚类中的差异最小化，同时避免（如果可能）单一化（聚类中只具有一个要素）。在每次迭代时，将通过这种剪除过程对其中一个最小跨度树进行分割，直至获得指定的聚类数。所采用的发布方法被称为 SKATER (Spatial "K"luster Analysis by Tree Edge Removal)。虽然在每次迭代时会选择可优化聚类相似性的分支进行剪除，但并不保证最终结果是最佳的。

从属度概率

计算成员关系概率的置换参数可定义置换检验次数以使用证据累积计算聚类成员关系概率。从属度概率包含在 PROB 字段的输出要素类中。从属度概率高表明此要素与其所分配到的聚类相似或相邻，您可以确信该要素属于其所分配到的聚类。从属度概率低可能表明此要素与其被 SKATER 算法分配到的聚类差别很大，或当分析字段、聚类大小约束或空间约束参数进行了某些更改，该要素可能包含在其他聚类中。

您指定的置换检验次数定义了为扰乱 SKATER 空间约束而创建的随机跨度树数量。随后该算法将针对为每个随机跨度树指定的聚类数进行求值。置换检验过程使用了由 SKATER 定义的原始聚类，可记录聚类成员在更改跨度树时聚集在一起的频率。易切换聚类的要素由于对跨度树的细微更改而从属度概率小，而不切换聚类的要素从属度概率较大。

对于较大的数据集来说，计算这些概率可能会耗费大量的运行时间。建议您首先进行迭代并为您的分析找到最佳聚类数，然后在随后的运行中计算分析的概率。您也可以通过将并行处理因子环境 设置增加到 50 来提升性能。

输出

空间约束多元聚类工具会创建许多输出。消息可从地理处理窗格进行访问，方法为将鼠标悬停在进度条上，单击工具进度按钮，或展开地理处理窗格底部的消息部分。您还可以通过地理处理历史访问之前运行空间约束多元聚类的消息。

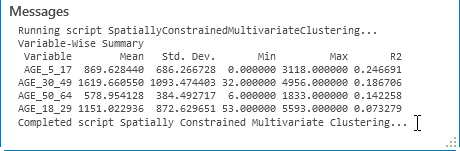
空间约束多元聚类工具的默认输出是一个新的输出要素类，它包含分析中使用的字段，以及一个名为 CLUSTER_ID 的用于标识每个要素所属的组的新整型字段。此输出要素类会添加到内容列表中，并会向 CLUSTER_ID 字段应用一种独特的颜色渲染方案。

空间约束多元聚类输出。

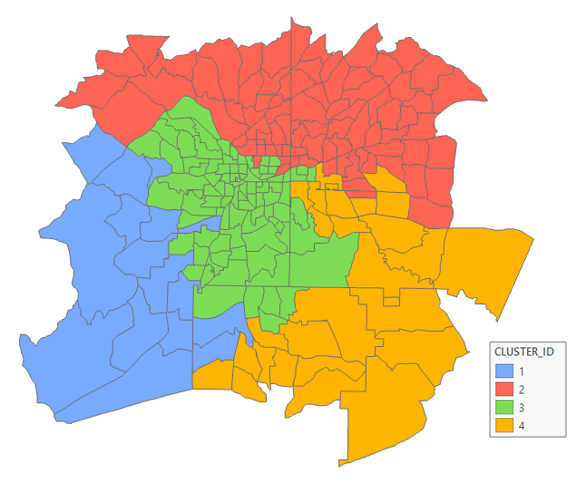
空间约束多元聚类图表输出

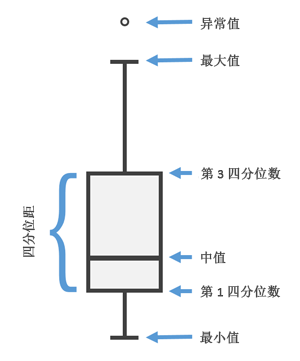
可创建多种类型的图表来汇总创建的聚类。箱形图用于显示关于每个聚类的特征信息以及分析中使用的每个变量的特征。下图显示了如何解读每个分析字段和创建的聚类的箱形图及其汇总值：最小数据值、第一四分位数、全局均值、第三四分位数、最大数据值和数据异常值（小于或大于四分位距 1.5 倍的值）。将鼠标悬停在图表上的箱形图上，即可查看这些值以及四分位数范围值。落在最小值或最大值（上须线或下须线）之外的任何点标记代表数据异常值。

抢先版本：

四分位距 (IQR) 是第三四分位数减去第一四分位数。低异常值将是小于 1.5*IQR (Q1-1.5*IQR) 的值，而高异常值将是大于 1.5*IQR (Q3+1.5*IQR) 的值。异常值在箱形图中显示为点符号。

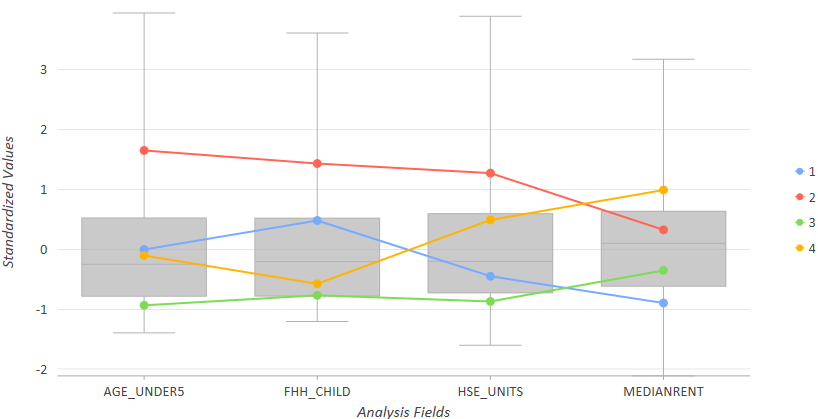
默认的平行箱形图图表汇总了各个聚类以及聚类中的各个变量。例如，对人口普查区域执行空间约束多元聚类工具创建 4 个聚类。在下面的图表中，请注意聚类 2（红色）反映具有平均租金、有孩子的女户主家庭的最高值 (FHH_CHILD)、住宅单元数量的最高值 (HSE_UNITS) 以及 5 岁以下儿童的最高值的区域。聚类 2（金鳞色）反映具有最高中值租金、有孩子的女户主家庭数量几乎最低、超出住宅单元平均数量的区域。聚类 3（绿色）反映了有孩子的女户主家庭最少、5 岁以下儿童最少、住宅单元数量最少和佣金几乎最低（不低于聚类 1）的区域。将鼠标悬停在平均线的每个节点上，查看每个分析字段的聚类平均值。

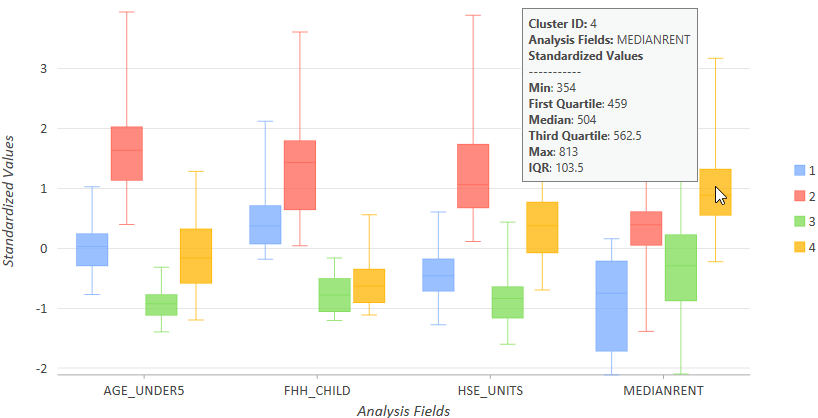
使用上面的平行箱形图检查分析的全局汇总后，可以通过在图表属性窗格的系列选项卡中切换为并排来检查每个变量的各个聚类箱形图。通过这种方式，可以了解哪个组中的每个变量具有最高和最低值范围。针对每个变量为每个聚类创建箱形图，以便查看每个聚类的值与创建的其他聚类的关系。将鼠标悬停在每个变量的箱形图上，以查看每个聚类中每个变量的最小值、最大值和中值。例如，在下面的图表中可以看到，聚类 4（金色）的 MEDIANRENT 变量具有最高值，并包含值为 354 到 813 的区域。

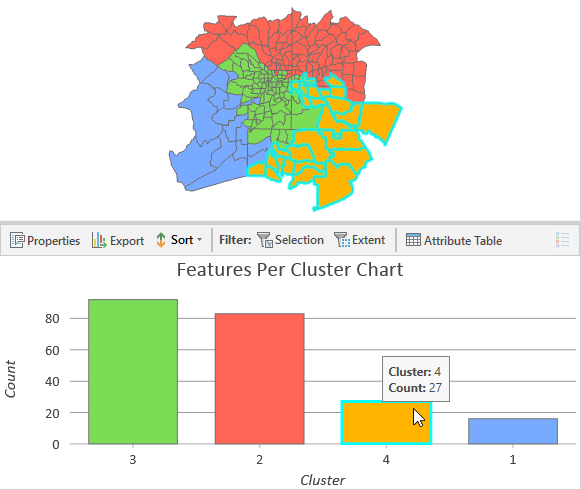
可创建一个显示聚类要素数量的条形图。选择每个条形图时也会在地图中选择该聚类的要素，这将有助于进一步分析。

当您将聚类数参数留空时，该工具将基于您的数据评估最佳聚类数。为聚类数评估输出表指定路径可创建一个显示伪 F 统计量计算值的图表。图表上最高的峰值是最大 F 统计量，表示使用多少个聚类来区分指定的要素和变量最有效。在下面图表中，与四个组相关的 F 统计量是最高的。具有较高伪 F 统计量的五个组也是不错的选择。

用于评估最佳聚类数的伪 F 统计量图表

最佳做法

虽然倾向于引入尽可能多的分析字段，但对空间约束多元聚类工具而言，最好从单个变量开始构建。较少的分析字段的结果更易于解释。而且，字段较少时，还易于确定哪些变量是最佳辨别因素。

在许多情况下，您可能运行空间约束多元聚类工具多次，才能查找到最佳聚类数、最有效的空间约束以及能够对要素进行最有效聚类的分析字段的组合。

如果工具返回 30 作为聚类的最佳数量，请务必查看 F 统计量图表。选择聚类数与解释 F 统计量图表也是一种艺术，较低的聚类数可能更加适合您的分析。

其他资源

Duque, J. C., R. Ramos, and J. Surinach. 2007. "Supervised Regionalization Methods: A Survey" in International Regional Science Review 30: 195–220.

Assuncao, R. M., M. C. Neves, G. Camara, and C. Da Costa Freitas. 2006. "Efficient Regionalisation Techniques for Socio-economic Geographical Units using Minimum Spanning Trees" in International Journal of Geographical Information Science 20 (7): 797–811.