需要 Spatial Analyst 许可。
计算直线距离并针对障碍和表面栅格进行相应调整后,即可确定遇到距离的比率。 成本表面是影响遇到距离的比率的 4 个因素之一。 其他 3 个因素为源特征、垂直系数和水平系数。
成本表面可捕获旅行者在景观中移动时会遇到的情况。 穿越田野比穿越森林容易,而穿越森林比穿越沼泽容易。 将成本表面上的每个值乘以调整后的直线距离,即可确定旅行者遇到该距离的比率。
作为成本表面的结果,旅行者可以在田野以比在森林或沼泽更快的速率覆盖调整后的直线距离单位。
直线距离采用线性单位,例如米或英尺。 在确定遇到距离的比率时,单位可以为美元、优先级、消耗的能量或风险。 比率是每单位距离测量的成本。

创建成本表面是一个多步骤过程。 首先确定将影响移动的条件。 然后将条件值变换为常见成本等级。 最后,对条件进行加权和合并。
这种分析称为最小成本分析。 成本表面也称为阻抗或摩擦表面。 覆盖高成本位置中调整后的直线距离单位将更加困难、更加昂贵或速度更慢。 创建成本表面可以类似于创建适宜性表面;但是,在适宜性表面中,将首选较高的值。 在成本表面中,较低的值更易于移动。
可以组合各种因素来创建成本表面。 例如,当针对动物移动创建成本表面时,诸如土地利用类型、与道路之间的距离以及与水的距离等因素将用于捕获动物在景观中移动时的优先级。 由于条件中的值具有不同的含义,因此在组合每个条件之前,必须将其变换为相同的成本等级。
在许多情况下,成本表面将针对成本距离分析定义成本单位。 源特征、垂直系数和水平系数是这些单位的乘数。 每个乘数应相对于成本表面中定义的相同成本单位。 如果指定了 4 个比率控制系数(成本表面、源特征、垂直系数和水平系数)中的多个系数,则仅其中一个系数可以具有单位,而其他系数是修改这些单位的无单位乘数。
借助成本表面,可以在实际景观上模拟旅行者。
成本表面用例
成本表面可用于解决各种情况,例如:
- 识别要建造一条通往拟建学校的道路的最小成本路径。 建造的成本表面单位为美元/米。
- 可以使用廊道连接野生动物栖息地,以允许物种在地区间活动。 成本表面单位是针对每个位置处通过要素的移动的每英尺优先级。
- 查找新的管线以连接油田和精炼厂。 成本表面单位基于管线将对每个位置产生的环境影响。
- 确定到达偏远地区受伤的徒步旅行者所在位置的最快方法。 成本表面单位为分钟/米。
整合成本表面
可以在概念上将距离分析分为以下相关功能领域:
- 计算直线距离,可以选择性地使用障碍或表面栅格调整计算。
- 计算直线距离后,可以选择通过成本表面、源特征、垂直系数和水平系数来确定遇到距离的比率。 创建累积距离栅格。
- 使用最佳网络、特定路径或廊道连接生成的累积距离表面的区域。
第二个功能区域中,通过成本表面确定将遇到距离的比率如下所示。 该方案包括 4 个护林员站(紫色点)和一些河流(蓝色线)的集合。
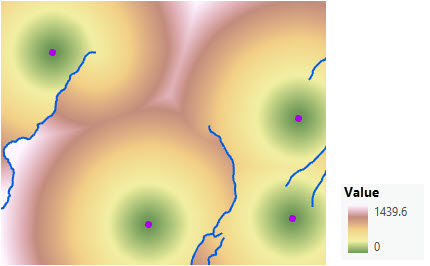
添加成本表面可以模拟旅行者在景观中移动。 请注意,在下图中,距离未从每个站均匀辐射。
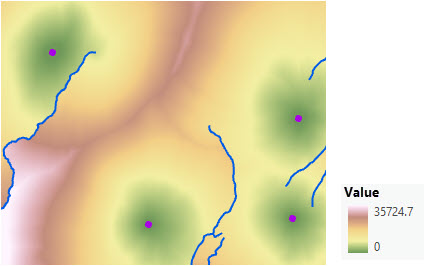
直线距离比率的成本表面
要创建成本表面来确定将遇到调整后的直线距离的比率,您将执行以下操作:
成本表面将影响遇到距离的比率
成本表面将基于位置处的要素来识别每个位置相对于移动的成本、阻抗、摩擦或优先级。 无论潜在应用或进行建模的成本单位如何,常规工作流都是相似的。
诸如建造、时间或能源的成本等绝对成本非常理想,但是可能难以针对每个位置对其进行定义。 但是,对于许多应用,不存在单个绝对成本单位。 例如,如果您要创建一个成本表面来识别两个位置之间的徒步路线或骑行车道,则仅针对成本单位使用能源或时间将不会捕获其他影响路线走向的因素。 这些因素可能包括风景、土地所有权以及避开对环境敏感的区域。 在针对创建野生动物廊道创造成本表面时,动物可能会在良好栖息地内移动与保持安全之间取得平衡。 在这两种情况下,都不存在可以捕获移动决策范围的单个成本单位。
在这些情况下,将使用相对主观的成本单位,例如优先级、安全性和风险。 每个条件值都将分配给一个常见成本等级,分配的成本基于主观单位彼此相对。 即,成本为 10 的移动难度是成本为 5 的两倍。 每个条件中的每个值都将位于相同的常见成本等级。
如果成本表面定义了成本分析的单位,则其他比率控制因素(源特征、垂直系数和水平系数)是修改指定成本单位的无单位乘数。
可以使用任意数量的 Spatial Analyst 工具直接分配绝对成本单位。 在定义主观成本单位以创建成本表面时,通常使用以下所述的工作流。
成本表面工作流
指定相对成本时用于创建成本表面的工作流如下:
- 确定影响移动成本的条件并收集基础数据。
- 根据需要从基础数据中获取条件。
- 将每个条件的值变换为常见成本等级。
- 相对于彼此加权条件,并对其进行组合以创建成本表面。
创建成本表面后,可以在该成本表面上使用最小成本路径连接区域。
如前所述,创建成本表面将遵循与创建适宜性表面相似的步骤。 它们之间的常见步骤是确定条件,收集基础数据,从基础数据中获取必要的条件,将条件值变换为常见等级,对条件进行加权并组合条件。 与在最终适宜性表面中首选较高的值不同,在成本表面中,将针对移动首选较低的值,因为它们表示较低的成本。 成本表面用于最小成本分析。 因此,在实施变换时,针对移动更加首选的位置将收到较低的值。
在以下部分中,将介绍此工作流的示例应用。 目的是确定短尾猫在栖息地之间移动的野生动物廊道。 该工作流仅用于演示用途,并不会实际定义所有短尾猫的交互行为。 可以将上述工作流用于为许多其他应用创建成本表面。
定义目标和成本单位
首先,定义移动的目标。 目标将有所不同,具体取决于要解决的问题。 例如,用于定位电力线的成本表面的目标可能是最大程度降低建造电力线的成本。 当确定消防员在两次火灾之间移动资源的路径时,目标可能是尽快在两次火灾之间移动。 对于短尾猫场景,成本表面的目标是允许短尾猫在栖息地之间安全地移动,同时保持对某些资源的访问。
接下来,必须确定成本单位。 对于确定电力线的位置,可以根据建造成本来变换每个条件。 对于确定消防路径,成本单位可能为时间。 对于短尾猫廊道,定义单位存在两个挑战。 一个挑战是缺少客观的可测量成本单位。 另一个挑战是条件具有不同的目标。 例如,与河流的距离条件是对水的需要,而与道路的距离条件是要保持安全。 在这种情况下,必须针对相对主观的优先级成本等级变换条件,然后才能对其进行组合。
确定目标和单位后,必须建立用于评估模型结果的方法。 在短尾猫成本表面中,要确定生成的路径是否成功,可以转至廊道并查看短尾猫是否正在使用这些路径在栖息地之间移动。
下图说明了短尾猫成本表面的创建:
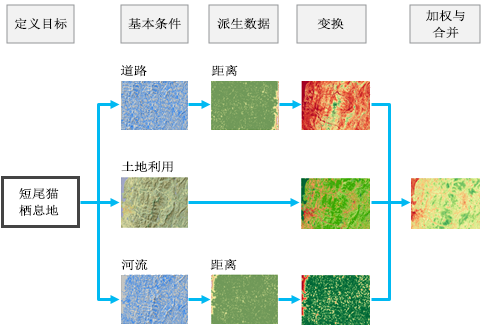
确定影响移动成本的条件
定义分析的目标、单位和评估方法后,创建成本表面的第一步是确定用于定义移动的条件。 在本示例中,该条件是短尾猫在景观中移动时首选的事物。 所确定的每一个条件都应有助于达到模型的总体目标,即确保短尾猫在获取关键资源的同时,能够在栖息地之间安全地移动。 所确定的条件应能够捕获短尾猫与其移动需求的相互作用。
在该简化的短尾猫示例中,将考虑以下条件:
- 土地利用类型 - 短尾猫喜欢在森林中穿行,而不喜欢在发达或半发达地区移动。
- 与道路的距离 - 出于安全目的,短尾猫喜欢在离公路较远的地方移动。
- 与河流的距离 - 出于对水的需求,短尾猫在景观中移动时喜欢停留在靠近水源的地方。
根据需要从基础数据中获取条件
某些条件(例如短尾猫示例中的土地利用类型)可以直接用于创建成本表面。 短尾猫将直接响应不同的土地利用类型。 您还可以获取其他条件。 请记住,并非道路或河流本身是条件,而是短尾猫响应的与道路或河流的距离是条件。
由于最初不存在与道路和河流距离的数据集,因此可以使用相应的 Spatial Analyst 工具从基础数据中获取这些条件。 对于,可以使用距离累积工具,针对道路条件确定每个位置与最近道路的距离,然后再次使用该工具,针对河流条件确定与河流的距离。
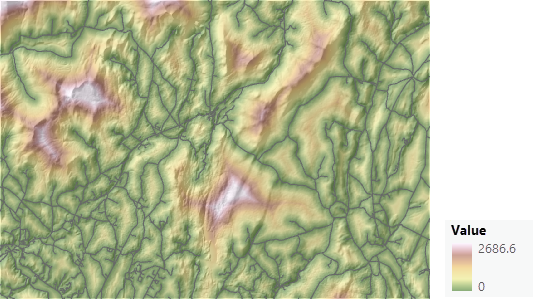
将每个条件的值变换为常见成本等级
仅通过数学方法将土地利用、与道路的距离以及与河流栅格的距离相加所得到的值没有任何意义。 例如,某个特殊位置的土地利用值为 4,代表单户住宅。 与道路的距离为 627 米,与河流的距离为 2,252 米。 将这些值相加得到 2883,这个数字完全没有任何意义。 在将条件栅格加在一起之前,必须将每个条件中的值变换为常见成本优先级等级。
在本示例中,将使用 1 到 10 的常见成本等级。 对于条件中的每个值,具有最容易或最首选移动特性的位置将获得较低的成本值,而更困难或非首选的位置将获得较高的成本值。 例如,由于短尾猫喜欢远离道路移动,因此距离道路 100 米以内的位置最不首选,它将获得成本 10,可以为距离道路 100 至 300 米之间的位置分配成本值 5,而距离道路大于 300 米的位置可以获得成本 1。
将每个条件中的值变换为 1 到 10 的成本等级时,请在等级内将这些值相互参照进行变换。 也就是说,分配成本值为 3 的位置的优先级将是成本值为 6 的位置的 2 倍,而成本值为 10 的位置的出行难度将比成本值为 1 的位置高 10 倍。
此变换过程将应用于针对成本表面确定的每个条件中的每个值。 针对短尾猫模型的土地利用条件,系统将为首选土地利用类型(例如森林)分配成本值 1(首选且移动成本较低),为住宅分配成本值 5,并为工业分配成本值 9。 对于与道路的距离条件,距离道路较近的位置将获得较高的成本 9 和 10,而距离道路较远的位置将获得较低的成本值(因为短尾猫更喜欢穿过这些位置)。 对于与河流的距离条件,更首选靠近河流移动,因此附近位置将获得较低的成本 1 或 2,而较远的地位置将获得较高的成本 9 或 10。
理想的情况是所分配的成本在各个条件之间的优先级均相同。 也就是说,所分配成本为 5 的经过变换的与道路的距离与同样被分配了成本 5 的土地利用类型或与河流位置的距离具有相同的优先级。
要变换条件,通常使用重分类和按函数重设等级工具。 在这些工具中,将为每个条件指定相同的成本等级。 对于本示例,将使用 1 到 10 的成本优先级等级。
土地利用类型是分类数据,将使用一对一变换将土地利用类型映射到成本。 将使用重分类工具。 在重分类表中,将为森林分配 1,并为工业分配 9,依此类推。
| 值 | 新建 |
|---|---|
农业 | 2 |
裸露土地 | 1 |
高强度开发地区 | 9 |
低强度开发地区 | 5 |
中等强度开发地区 | 8 |
针叶林 | 1 |
落叶林 | 2 |
混合落叶-针叶林 | 2 |
草原 | 4 |
灌木丛/灌木 | 3 |
水域 | 10 |
Wetland | 9 |
NODATA | NODATA |
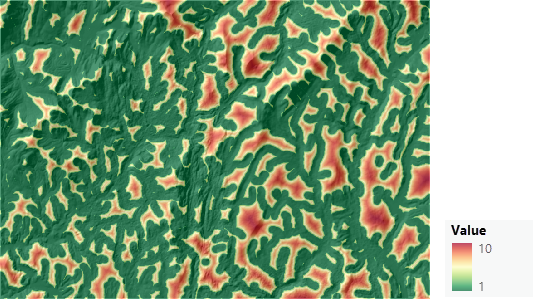
以下是生成的经变换的土地利用地图。 绿色位置的优先级较高,而红色位置的优先级较低。

与道路的距离以及与河流的距离是连续数据。 要变换条件值以捕获成本交互作用,需要应用函数。 随着短尾猫远离道路,其优先级或成本将根据指定函数而不断下降。
按函数重设等级工具的重点是用于适宜性建模,其中,首选属性越多,其值越高。 在最小成本分析中,逻辑则相反。 将为优先级更高的区域分配较低的值,指示较低的成本。 按函数重设等级工具可以通过以下两种方式之一在逻辑上适应这种反转:
- 在工具中选择适宜性函数的反函数。 也就是说,可以在适宜性模型中将 Small 函数应用于与河流的距离条件,指示距离河流更近的条件更加适合,从而获得更高的值。 如果将与河流的距离用于成本表面,则将使用 Large 函数,指示距离更远的位置将获得更高的值(非首选)。 距离更近的位置将获得更低的值(成本更低),并且优先级更高。
- 可以反向应用适宜性模型中所使用的相同逻辑。 于适宜性模型的与河流的距离条件,以及在变换成本表面的与河流的距离条件时,可以指定 Small 函数。 但是,对于成本表面,必须将自等级和至等级参数从 1 至 10 反转为 10 至 1。 因此,较近的位置现在将获得至等级值,该值现在为 1,因为其移动成本最低。

要捕获短尾猫要在河流附近移动的首选项,对与河流的距离条件应用了不同的函数。
如果在将条件值变换为成本(例如建造成本或时间)时使用绝对成本单位,则可以使用直接分配或数学公式。 可以使用栅格计算器来应用这些公式,而非应用以上相对变换步骤。
提示:
成本值必须始终为正值;输入成本栅格的像元值不能小于或等于 0。 如果存在这样的值,则可以将整个范围重设为大于 0 的等级,或者将问题值替换为较小的正数。 可使用条件函数工具执行此操作。 如果值为 0 的区域代表应从分析中排除的区域,那么在运行距离累积前,应将这些值更改为 NoData。 可以使用设为空函数工具执行此操作。
现在,每个条件中的值都将相互参照变换为常见成本等级,并且可以对经变换的条件进行组合。
相对于彼此加权条件,并对其进行组合以创建成本表面
将三个经转换的条件加在一起时,所生成的范围可以是 3 到 30。 所分配值为 3 的位置为优先级最高的移动位置。 将为森林中远离道路且靠近河流的位置。 所分配值较高的位置将为优先级较低的位置(移动成本较高),具体取决于该位置的要素情况。
但是,对于短尾猫的移动成本而言,在将这些条件汇总到一起之前,可能存在一个条件其他条件更重要或更显著的情况。 如果真是这样,那么该条件的权重应大于其他条件的权重。 为了强调区别,变换过程会将一个条件中的值相互参照进行转换。 权重将定义每个条件相对其他条件的重要性。
权重是应用于条件中每个经转换的值的乘数。
在短尾猫适宜性模型中,将较高的权重应用于条件表明该条件对短尾猫的生物学更加重要。 但是,在成本表面中,权重指示该条件比其他条件更加重要或者移动成本更高。
在短尾猫成本表面中,出于安全目的,可以确定短尾猫要避免在道路附近移动。 因此,将为经转换与道路的距离条件分配的权重将高于与河流的距离条件。 例如,由于某个位置接近道路,因此最初可能针对与道路的距离为其分配成本 10。 由于该位置也接近河流,因此可能针对与河流的距离为其分配成本 1。 如果将权重 1.5 应用于与道路的距离条件,而为与河流的距离条件分配权重 1,则该位置将在结果成本表面中获得总成本值 16(10 x 1.5 +1 的结果)。 因此,距离道路较近的位置,成本较高,并且优先级较低。
在本示例中,还将为土地利用条件分配权重 1。

由于具有权重,因此有时会将最小成本分析称为加权最小成本分析。
注:
如果使用绝对可测量的成本单位,例如美元或时间,则不会应用权重。 即使一个条件的重要性可能更高或更低,但是绝对成本也不会改变。 美元成本或时间为实际成本。 如果应用权重,则绝对单位将不再有效,并且成本将处于相对等级。
现在已创建成本表面。 根据每个位置的特性,成本表面将从短尾猫的角度指示每个位置与其他位置相比的优先级。 短尾猫模型的最终目标是将一系列短尾猫栖息地与野生动物廊道连接在一起,从而形成累积成本栅格,以便短尾猫在它们之间移动。
可通过以下方式连接栖息地:
- 创建最小成本网络(请参阅使用最佳网络连接区域)。
- 将特定栖息地彼此连接(请参阅使用最佳路径连接位置)。
- 使用廊道连接栖息地(请参阅使用廊道连接位置)。
坡度和成本表面
对于遇到调整的直线距离的比率,成本表面是可以控制该比率的 4 个因素之一。 在成本表面中,无论是从东向西、从西向东、从北向南、从南向北穿过该像元,还是沿任何对角线方向来回移动,成本都是相同的。 但是,对于旅行者来说,他们在哪个方向上通过该像元可能非常重要。 上坡和下坡需要不同的努力。 因此,如何遇到坡度可能非常重要。 例如,如果您移动到具有陡峭坡度的位置,并且垂直于那些坡度移动(沿轮廓线移动),则所需的努力小于直接沿陡峭坡度向上的努力。
坡度工具将通过确定从处理像元中心的高度到 8 个相邻像元中心的每个像元中心的高度上升幅度来计算坡度。 会将 8 个坡度中最陡的坡度分配给该像元。 由于为像元分配了最大下降,因此其无法捕获到该像元中的任何移动方向。 在对移动进行建模时,某个位置处的坡度陡峭程度可能无关紧要,但是遇到该坡度的方式可能非常重要。 如果在成本平面中使用坡度栅格,则旅行者可能会不必要地避开已分配陡坡的像元。
通常,如果旅行者遇到坡度的方向非常重要,则需要通过垂直系数,而非通过成本表面来捕获该方向。 坡度通常被错误地用作成本表面中的输入条件。
但是,在某些情况下,坡度栅格适合包含在成本表面中。 例如,您要定位一条新的徒步路线,并且像元中的坡度非常陡峭,因此无论旅行者进入像元的方向如何,坡度都会降低旅行者的速度。 在这种情况下,坡度的方向性无关紧要,因此坡度栅格适合包含在成本表面中。

对旅行者而言,重要的是他们如何遇到坡度,而不是坡度的陡峭程度。 沿陡峭坡度向上将需要最大的努力,下坡需要的努力最小,而在具有坡度的某个位置移动所需的努力居中。 与坡度相结合的土地覆被也会影响移动。 在比较粗糙的自然地面上移动比在道路上行驶更加困难。 步旅行者将根据他们克服遇到的坡度和土地覆被的容易程度来进行颜色编码。 绿色数字的出行速度比红色数字更快。
速度控制因素中的单位
计算经调整的直线距离后,可以通过成本表面、源特征、垂直系数和水平系数来控制遇到这些距离单位的比率。 每个系数都是调整后的直线距离的乘数。 指定系数的单位时必须格外小心。 成本表面不能采用优先级为单位,垂直系数不能采用时间为单位。 单位必须一致。
通常,成本表面是比率分析的驱动单位。 垂直系数、水平系数和源特征通常是成本表面的成本单位的无单位乘数。
使用垂直系数应用 Tobler 的徒步旅行功能时,情况并非如此。 在徒步旅行功能中,单位为时间并成为成本分析的驱动单位。 如果将成本表面添加至分析,则成本表面值必须为无单位乘数,从而能够在考虑垂直系数的斜率的同时,修改通过景观的时间。
使用 模型构建器 创建成本表面
模型构建器 是一个创建成本表面的有效环境。 可提供链接输入和输出条件以及地理处理工具的功能。 借助模型的图形表示,可以直观地呈现模型的逻辑,并且可以随时进行更改并重新运行模型。
在创建可能包含不同移动目标的复杂成本表面时,经常会使用子模型。 子模型不仅可以组织模型目标,而且可以针对某些条件使用不同的转换来满足不同的移动目标。 例如,在短尾猫示例中,当转换土地利用类型时,对于资源子模型,移动到场地的边附近可能会比较有利,但是对于安全子模型,则相反。
其他成本表面应用
以下将演示如何使用成本表面来解决其他类型的应用。
无尾流区
可以使用成本表面来表示通过港口无尾流区的最大步速。 海岸线周围 100 米缓冲区的最大速度为 5 节,最大步速为 1h/(5*1.852)km。 100 至 200 米之间的缓冲区廊道的最大步速可能为 1h/(10*1.852)km。 请注意,随着速度的增加,步速将降低。
道路建造成本
要评估一条新道路的总建造成本,可以创建一个成本表面,用于对每英里建造成本进行编码。 在农村地区建造一条新的两车道无分隔道路比在城市地区建造一条相同的道路便宜。 在本例中,可以将成本表面中的像元划分为城市与农村。 根据美国道路交通建筑工协会 (ARTBA) 常见问题解答中的信息,农村地区每英里成本的典型值为 200 万美元/每英里,城市地区每英里成本为 400 万美元/每英里。 此外,可以根据当地分区和财产法添加障碍。
其他信息
以下部分包含有关成本表面的其他信息。
考虑移动的一年中的时间
一年中的时间可能会改变成本表面。 移动的成本表面是在冬季、夏季、旱季还是雨季? 移动是针对晴天还是恶劣天气,针对极端事件还是典型情况?
其他时间影响是否在影响移动? 对于野生动物成本分析,移动是针对到达产犊地点,还是针对栖息地之间的日常移动或季节性迁徙? 移动是否处于狩猎季节?
影响移动的各种时间因素可能不仅会影响转换和权重,还可能会影响成本表面中将使用的条件。
要捕获各种季节性类型和移动类型,您可能需要多个成本表面,并对每个成本表面执行距离分析。 您可能需要组合结果以捕获全年的移动需求。
将道路或路径整合到成本表面中
考虑一个成本表面,救援人员将在全地形车 (ATV) 上使用该成本表面以到达受伤的徒步旅行者所在位置。 对于本示例,条件将为土地利用类型、坡向和坡度。 沼泽地将为高成本,而草地将为低成本。 由于此次救援在春季进行,因此朝南坡向更加泥泞且成本更高,而冰冻朝北坡向成本更低。 可以通过垂直系数来整合克服坡度的难度。
遇到道路时,成本会发生变化。 在道路上行驶更加快捷轻松。 在道路上行驶的成本是较低的固定成本。
要捕获道路的固定较低成本,在创建成本表面后,道路随即整合到成本表面中。
- 可以使用折线转栅格工具对道路进行栅格化,然后为道路分配单个成本。 如果道路要素数据集没有成本字段,则需要对值大于等于 0 的任何字段进行栅格化,例如 FID,然后在栅格计算器工具中应用以下表达式:Con(rasterRoads >= 0, 50)
50 为分配的成本。 生成的栅格将命名为 roadCostValue,并在下一步中用作表达式的输入。
如果适用,则成本可能会因道路类型而异。
- 可以使用栅格计算器工具列表中的 Con 和 IsNull 工具将 NoData 值转换为零。 请使用以下形式的表达式:Con(IsNull(roadCostValue), 0, roadCostValue)。
生成的栅格将命名为 roadCost,并在下一步中用作表达式的输入。
- 可以使用栅格计算器将道路整合到成本表面中。 请使用以下形式的表达式:Con(roadCost > 0, roadCost, costSurface)
在最终输出栅格中,将为道路经过的像元分配与道路相关的成本。 所有非道路像元都将获得在成本表面中创建的成本值。
因此,ATV 将穿过景观,当它遇到道路时,它将在该道路上行驶尽可能长的时间,然后离开该道路到达受伤的徒步旅行者所在位置。 对于陡峭和弯曲的路段,道路成本可以进一步优化。
加粗障碍以防止裂缝
可以将成本较高或者成为障碍的线性要素(例如道路或河流)整合到成本表面中。 如果线性要素为折线,则将对其进行栅格化。 当表示为栅格时,线性要素的厚度将仅为一个像元。 虽然可以在完全水平或垂直的位置保留障碍的性质,但其可能是对角线部分。 在这种情况下,旅行者可能会在几何上滑过相应部分,这些部分相当于障碍中的裂缝。 如果出现这种情况,则障碍或高成本像元将不再是移动的阻碍。

要将线性要素添加至成本表面,请完成以下步骤:
如果输入线性要素为栅格,则将使用相同的步骤。 无需首先栅格化线性栅格要素。 可以使用距离累积工具并设置最大累积(距离)值,在栅格要素周围创建缓冲区。
如果线性要素还不是栅格,则可以对其进行栅格化,而非对其进行缓冲。 然后,在指定统计数据的栅格化线性要素上运行焦点统计工具。 如果选择 3×3 邻域,则该工具将在要素的任一侧将线性要素加宽一个像元。 分配的像元值将基于指定的统计数据。 然后可以将生成的表面添加至成本表面,如前一部分所述。 如果线性要素为栅格并且其表示诸如深度、盐度、pH 或距离等梯度,则此方法特别有用。
注:
如果要将较高的成本分配给相对成本等级中的线性要素,请确保分配的成本相对于最终成本表面中的总和值。
但是,如果该线性要素为真实的障碍,则在将像元组合到成本表面中之前,需要为其分配 NoData。 如果该线性要素为真实的障碍,则最好通过距离累积工具中的障碍参数来输入该线性要素。
使用“适宜性建模器”创建成本表面
虽然可以使用单个地理处理工具来创建成本表面,但是需要追踪所使用的工具和指定的参数,以便进行后续更改。 建议使用 模型构建器 创建成本表面。
还可以在 Spatial Analyst 适宜性建模器中创建成本表面。 如果您使用“适宜性建模器”来创建成本表面,请记住,在适宜性模型中,条件值越有利,其获得的适宜性越高。 成本表面用于执行最小成本分析。 更易于移动或成本更低的区域将获得较低的值。
“适宜性建模器”中的唯一类别和类范围转换方法可将成本值一对一地分配给类别或类。 在连续函数变换方法中,需要应用与适宜性模型中相反的函数。 例如,如果距离河流更近在适宜性模型中的优先级更高,则可以应用 Small 变换函数。 较小或较近的位置将获得较高的适宜性值。 如果在成本曲面中移动到河流附近更可取或成本更低,则可以选择 Large 函数。 更远的位置将被转换为更高的值,即成本更高。 距离更近的位置将获得更低的值,即成本更低并且优先级更高。
或者,可以使用与适宜性建模相同的逻辑来选择连续函数。 优先级更高的位置将获得更高的值,但在成本表面中,优先级更高的位置应获得更低的值。 要反转成本表面的值,请在连续函数方法中使用反转函数参数。