距离累积和距离分配工具取代了传统成本距离工具。 这些新工具通过重建连续的累积表面来测量各个方向的成本距离,而不是通过像元中心网络寻找路径。 您可以从输入成本摩擦表面和其他参数创建输出累积成本表面。 与其他表面一样,您可以通过添加等值线(累积成本相等的线)、将其在 3D 模式下进行可视化或结合分配流域进行可视化来更精确地了解结果。 通常情况下,构造此表面的目标是绘制最低成本路径,也就是下降最陡的路径。
累积成本表面
这些工具使用的算法将通过其坡度重建表面。 相比使用基于像元中心网络的方法,这种方法将提供更好的结果。
传统网络路径方法
在传统的成本距离工具(成本分配、成本回溯链接、成本距离、路径距离、路径距离分配和路径距离回溯链接)中,会将输入成本栅格中的像元值进行成对组合,并将结果作为边权重分配到通过像元中心连接的网络上。 有关详细信息,请参阅成本距离工具工作原理和路径距离工具的工作原理。 网络最短路径算法使用这些边权重沿网络找到从每个源到分析区域内的每个其他像元的最小累积成本路径。 该网络路径的加权长度被记录为每个非源像元的最低累积成本。
在这种方法中,无法找到直线最短路径。 例如,在下图中,当所有边权重都等于 1 时,最短网络路径是 A-B’-B,而不是 AB。
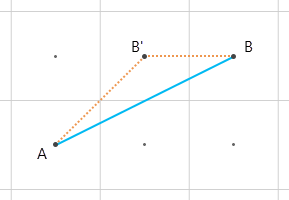
此博客文章包括网络畸变的地理示例。
表面重建方法
使用距离累积和距离分配工具,查找累积成本不再是网络问题。 输出累积成本栅格是一个形状未知的表面。 您想在仅提供研究区域内每个像元坡度的情况下发现该形状。 这种方法使用微分几何中的概念来消除“8 个方向”问题,从而可以计算所有方向的真实距离和成本。
累积成本表面可以回答三个重要问题:
- 在何处成本随距离快速增加?
- 哪些源像元与给定非源像元最近?
- 从一个非源像元到最近的源像元应该遵循哪条路径?
您可以将 3D 视图和等值线和输出表面配合使用来寻找这些问题的答案。 您可以使用距离分配和最佳路径为线工具来获得更加精确的答案。
以下小节描述了简单输入成本摩擦表面和输出累积成本表面之间的关系。
简单输入成本摩擦表面
考虑一个简单的成本摩擦栅格,其中心部分的成本 = 3,中间部分的成本 = 2,外部的成本 = 1。

可以使用 3D 解释了解成本摩擦栅格与输出累积成本表面之间的关系。 像元 c 处的表面高度 h 是输入成本栅格的坡度总和乘以这些坡度的有效距离 (h = 3 * d1 + 2 * d2 + 1 * d3)。
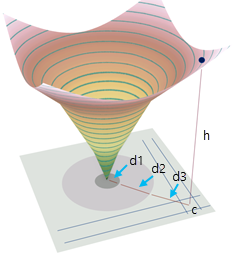
同一输出表面的平面视图显示了等值线如何描绘累积成本变化。 同时显示像元位置 c 处的坡度和坡向值。 坡向(最陡下降方向)始终与等值线成直角。

整合最低累积成本
下面是一个稍微复杂的案例。 非源像元处的累积成本(高程)将来自于到达该像元所用成本最低的源。
成本栅格包含两个值:1 为浅灰,3 为深灰。 源点为 S1 和 S2。 根据累积成本,非源像元 D 与 S1 更近。
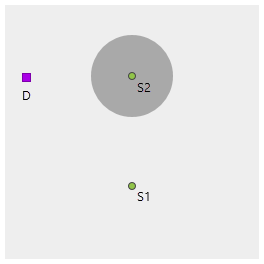
将等值线添加到累积成本表面可以帮助您看到在远离源时成本将如何快速变化。 从非源点开始与等值线成直角移动,即可回到最近的源像元。 路径未通往几何上最近的源,因为源周围的成本较高。
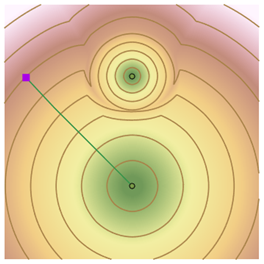
下方的 3D 视图显示同一最低累积成本表面。 成本较高的源周围表面更陡(成本累积更快)。 拥有最低成本表面的源与之非常接近。 在研究区域的所有其他像元中,表面由左侧的源所有。
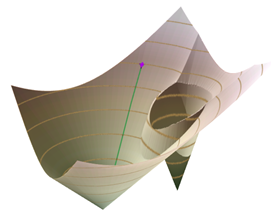
分配区域作为流域
当输入成本摩擦表面和输出累积成本表面变得更加复杂时,您仍然可以使用等值线、坡度和坡向来理解累积成本表面的行为。 此外,源周围的分配区域可作为累积成本输出表面上的流域。 一个分配区域内的所有最低成本路径都流向同一个源。 在下方示例中,分配流域将与等值线和 3D 视图相结合。
诸如此行驶时间表面等更复杂的累积成本表面可以使用等值线(本例中为等时线)在 2D 和 3D 模式中精确地可视化。
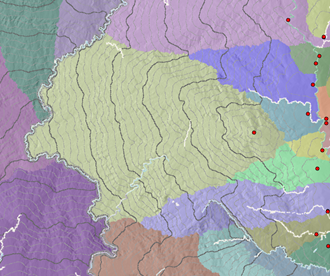
下图显示同一表面的 3D 视图。 背景中的悬崖是由于存在河流而造成的障碍。
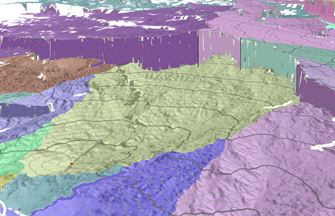
最低成本路径沿累积成本表面流向定义分配区域(流域)的源,如下图所示:
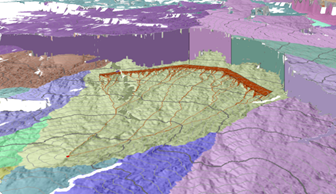
表面重建算法是网络算法的扩展
要想仅使用各个像元处最陡坡度的知识来寻找累积成本表面,您也可以使用表面重建算法。 这种算法类似于传统成本距离工具所使用的最短路径算法,但增加了一个步骤,用于提供一个不遵循八个网络方向之一的累积成本近似值。 此步骤称为程函步骤。 以下内容仅进行简单介绍,Sethian (1999) 的著作中提供了详细信息。
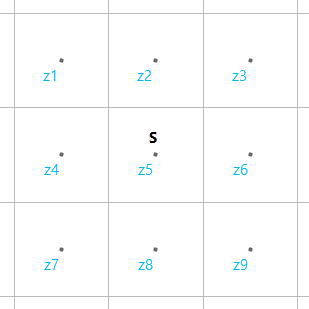
要在上下文中了解此步骤,您将看到下方中心像元的累积成本 z5。 假定您了解所有相邻累积成本 zi。 同样,您从输入成本栅格中了解了中心像元处的坡度值 S。
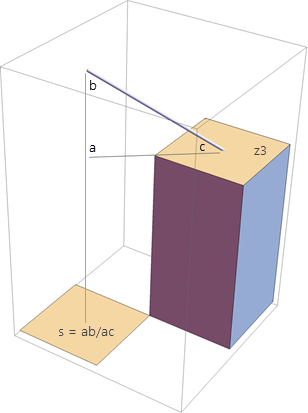
例如,z5 的一个近似值可能沿着 z3 和 z5 之间的对角线分布,其中 z5 = z3 + 1.4 * 像元大小 * S,如下图所示。 在本例中,输入成本栅格的值 S 将被视为三角形 abc 的坡度。 对于所有类似的网络样式近似值,仅使用 z5 处的坡度来估算 z5 处的累积成本。 这与传统网络算法不同,将使用像元对的平均成本。
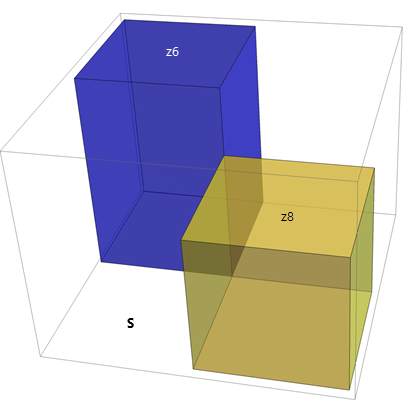
可以得出八个网络近似值,其中四个近似值使用成对的现有高度,如下方的三幅图所示。 在这种情况下,像元 z5 位置处的输入成本栅格值将被视为穿过两个已知点和未知高程 z5 的平面的倾斜度 S。 根据此关系,您可以对 z5 求解。 这就是程函步骤。
将计算平面的倾斜度。
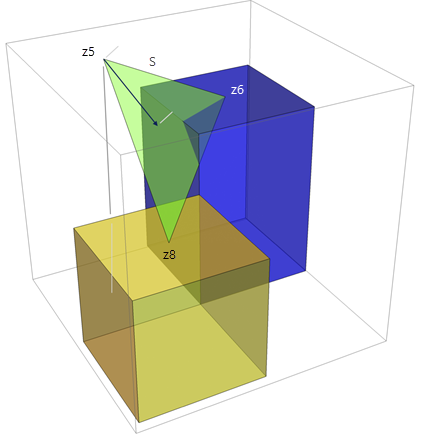
将计算倾斜的方向。
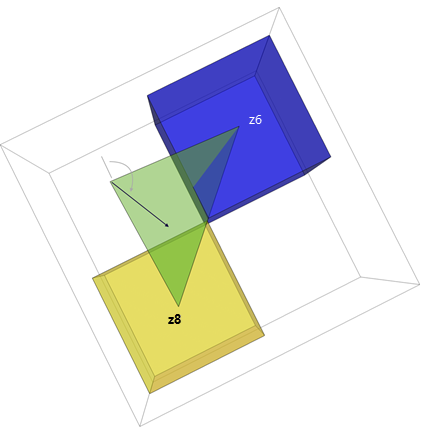
程函步骤还可以恢复 z5 处的坡向信息,称为反向。
在中心像元处现存在高程的 12 个近似值。 将选择其中的最小值,记录为中心像元的累积成本值 z5。 如果您需要反向栅格,倾斜的坡向(如上一段落中所述)将记录在输出反向栅格的相应位置。
每一次为像元的相邻像元获取高程值时,都将对像元重复此过程。 最终,高程值将不再变化,算法随即结束。 初始高程由源提供:可能是零或是每个源的初始累积值。 另一个初始高程值设置为无穷大。 Sethian (1999) 的著作中提供了详细的描述。 此方法的 Esri 实施是 Sethian (1999) 和 Zhao (2004) 的著作中所述方法的组合。
总之,从各个像元的坡度开始,这些步骤既重建了累积成本表面的高程,又重建了最陡下降的方向。
最低成本路径
最低成本路径在累积成本表面上遵循最陡下坡方向。 像元的方向如上方图 8 中所示。 输出反向栅格存储各个像元的方向。 您可以使用最佳路径为线工具,将反向栅格作为输入来绘制以非源像元为起始的路径。
在下图中,显示了一条从右上方的蓝色非源像元 d 到下方源像元 s 的弯曲的最低成本路径。 虽然 d 在几何上更接近于顶部的源,但由于该源周围成本较高,所以沿弯曲路径前往 s 成本更低。
目的地 d 是蓝色的方形。 通过绕过高成本的源,路径通过成本较低的区域到达成本最低的源。
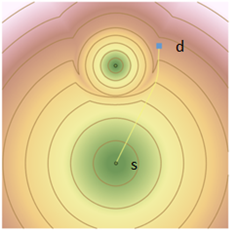
虽然此名称看起来可能有悖常理,但最低成本路径构建的输入位置称为目的地。 这些源用于构建表面,是最低成本路径的终止位置。
源周围的分配区域进一步说明了从目的地出发的最低成本路径将前往底部的源而非顶部的源。 接下来,所选区域将放大以显示如何解释反向栅格中的像元值。
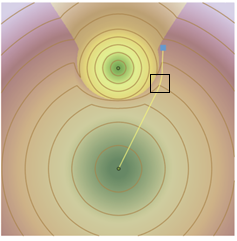
连接反向像元中心的格网以深灰色显示。 像元边界以浅灰色显示,像元值显示为方位角箭头。 当最低成本路径与格网线交叉时,将使用行进方向中最近的反向像元中的方位角来更新其方向。 在像元 a 旁边的顶部路径顶点处,将使用存储在 a 中的反向值引导离开顶点的线。 下一个将要交叉的格网线距像元 b 最近,因此将使用方位角来离开第二个顶点,以此类推。
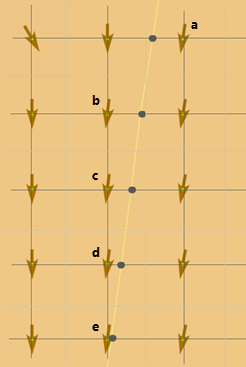
总之,最低成本路径在像元中心开始和结束。 其他路径顶点可以位于贯穿像元中心的水平线和垂直线格网上的任意位置。
有效坡度计算
上一部分中所述的坡度值并不严格来自于输入成本摩擦栅格。 还存在多个其他输入,它们共同确定了表面重建算法所使用的有效坡度。 关于这些输入的详细说明,包括通过像元的运动方向和从源出发或到达源的行进方向的重要性,将在其他专题中介绍。 此处的重点是表面重建算法如何使用输入。 输入如下:
- 成本摩擦输入,C
- 表面输入,S
- 源成本乘数,M
- 水平系数函数,HF
- 垂直系数函数,VF
重建算法使用的有效坡度具有以下一般格式:
有效坡度 = C * S * M * HF * VF
然后将该值乘以像元大小或 sqrt(2) * 像元大小,再将其添加到现有高度以获得其中一个网络方向的高度估计值。 将使用一个更加复杂的有效坡度函数来获得程函步骤的高度估计值。
有效坡度的单位必须是累积成本除以线性距离,即比率。 例如,如果您的累积成本表面以小时为单位来衡量行驶时间,且您的分析像元大小以米为单位,那么有效坡度的单位必须为小时/米。
由于有效坡度是多个项的乘积,您必须确保各个项的单位结合后可产生正确的有效坡度单位。 例如,如果您仅使用简单的成本摩擦栅格来描述与方向无关的行驶时间,则成本摩擦栅格像元值必须以小时/米为单位。 或者,如果您同时使用托布勒的远足函数作为垂直系数函数,那么远足函数的单位将是小时/米,而您的成本摩擦表面(如存在),必须视为无单位的权重。 您必须确保成本摩擦像元值能够以该方式解释。 换言之,垂直函数和成本摩擦不能同时是比率。
您不会直接控制表面输入 (S)。 这是一个无单位的权重,通过拉伸像元大小来覆盖像元中心之间的实际 3D 表面距离。 在图 2 中,表面重建算法使用中心像元处的输入成本摩擦栅格的坡度以及相邻像元的假定已知高度,通过创建多个中心像元高度的近似值来计算出该高度 z5。
障碍边缘相连
距离累积和距离分配工具中的障碍是无法穿过的输入像元。 这些像元在计算中表示为 NoData 像元。 它们可以显式地作为工具参数呈现,也可以隐式地作为 NoData 值呈现在其他栅格输入中(例如成本摩擦栅格)。 在第一个案例中,这些像元被栅格化并在成本栅格中变为 NoData。 由于表面重建算法无法降低障碍像元的高度估计值,所以会转而寻找其周围的路径。
表面重建算法将使用所有与像元相邻的八个像元以找到其高度估计值。 边缘相连障碍的相邻像元不会妨碍使用对角线相邻像元获取高度估计值。 在下图中,即使像元 z2 和 z6 是障碍,也可以通过 z3 得到 z5 的高度估计值。
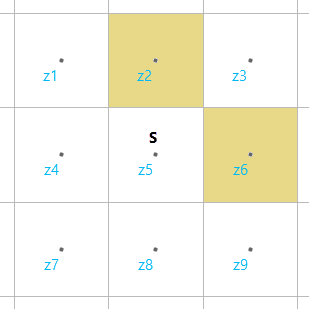
如果 z2 和 z6 旨在作为线性障碍要素的一部分(例如运河或河流),此行为会破坏障碍的意图。 为了防止这种情况的发生,表面重建算法倾向于连接障碍像元而不是连接非障碍像元。 这意味着将会在成本栅格中引入额外的 NoData 像元,以确保所有现有的障碍像元共享一条边。 在上图中,像元 z5 或像元 z3 也会变为障碍像元。
当您在分析中使用障碍时,请考虑此行为并相应地调整分析像元的大小,以保留障碍周围的预期连通性。 您可以使用焦点统计工具使线性要素的栅格版本更加复杂,从而将其作为障碍或线性网络使用,这些线性要素不应被相邻的障碍像元中断。
参考资料
Douglas, D. "Least-cost Path in GIS Using an Accumulated Cost Surface and Slopelines", Cartographica: The International Journal for Geographic Information and Geovisualization, 1994, Vol. 31, No. 3, DOI: 10.3138/D327-0323-2JUT-016M
Goodchild, M.F. "An evaluation of lattice solutions to the problem of corridor location", Environment and Planning A: Economy and Space, 1977, vol. 9, 727-738 页
Sethian, J.A. Level Set Methods and Fast Marching Methods (Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science) 2nd Edition, Cambridge University Press, 2nd edition (June 1, 1999)
Warntz, W. "Transportation, Social Physics, and the Law Of Refraction", The Professional Geographer, 1957, Vol. 9, No. 4, pp. 2-7.
Zhao, H. "A fast sweeping method for Eikonal equations", Mathematics of Computation, 2004, Vol. 74, No. 250, 603-627 页