需要 Spatial Analyst 许可。
可使用扩展和收缩工具概化或简化栅格。 与众数滤波和边界清理工具不同,扩展和收缩可用于将概化目标定位到特定的一个或多个区域。 根据所用工具,可以使特定区域更大或更小。 也可以控制将发生的概化量。
这两种工具都有两种方法可供选择。 第一种是数学形态学方法。 另一种是基于距离的方法。
比较扩展和收缩
这两个工具的操作方式均为允许某些区域替换其他区域的像元。
扩展
使用扩展时,所选区域通过扩展到其他区域中增加大小。 从概念上讲,所选区域值可视为前景区域,而其他值将仍保留为背景区域。 前景区域可扩展到背景区域。
收缩
使用收缩工具时,所选区域将相对于扩展到其中的其他区域按像元收缩或减小大小。 从概念上讲,所选区域值视为前景区域,而其余区域值视为背景区域。 通过此工具,允许使用背景区域中的像元替换前景区域中的像元。
此外,还可以替换区域中的小岛屿(可被视为与区域共用边界)
概化量
可通过像元数参数控制概化量。 默认情况下,此值为 1,这意味着根据所用工具,所选区域将按与一个像元大小对应的数量进行扩展或收缩。 要增加概化程度,可以为此参数指定较大的值。 从概念上讲,这与将该工具运行指定次数一样,其中上一次运行的结果是后续迭代的输入
方法
使用扩展和收缩工具概化栅格时,可以使用两种方法,即数学形态学方法和基于距离的方法
数学形态学方法
数学形态学方法将结构化元素应用于栅格以从中提取知识。 有几种可能的形状,最常见的形状是简单的 3 像元乘 3 像元正方形。 操作期间,将检查正在处理的栅格中的每个像元是否包含在所选区域集中(Matheron, 1967 和 Sera, 1982)。 算法已经从早期图像处理中的二进制图像处理演变为应用于具有多个区域值的输入并且结构化元素的大小可选。 对于此方法,“扩展”和“收缩”工具使用 3x3 正方形结构化元素。
基于距离的方法
基于距离的方法假设具有一个或多个所选输入区域值的像元为源。 输入栅格中的每个像元均视为与其距离最近的源像元的距离有关。 距离限制为输入栅格像元分辨率整数倍数的欧式距离。
需要评估以下条件才能确定该距离内任何特定像元的最终输出值。 虽然描述是针对扩展工具的,但是同样的原则也适用于收缩工具。
- 如果像元只能在允许的距离范围内查找一种类型的区域源像元,则将按照该区域值扩展到该像元内。
- 如果像元在允许的距离内具有多种类型的区域值,则将按照最近区域的值扩展到该像元内。
- 如果像元在允许的距离内有几种类型的源像元,并且有两个或多个源像元具有相同的距离(平局),则该算法将首先计算每个源区域的贡献。 总贡献最大的区域将用作该像元的输出值。
- 如果仍然存在平局,则表示存在两个或多个最近且贡献相同的源区域。 在此情况下,像元值最小的源将扩展到该像元内。
示例
下面是将工具对应的扩展方法或收缩方法参数设置为默认的形态学选项时使用这些工具的示例。
扩展示例
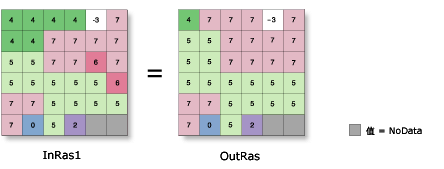
在下图中,扩展工具被应用于输入栅格,区域 5 扩展了一个像元。 请注意,区域 5 已扩展到右下角的 NoData 值。

收缩示例
在下图中,收缩工具应用于输入栅格,因此区域 5 将收缩一个像元。 5 区在任何区域的宽度不超过两个像元;因此,所有包含 5 的像元都将被替换为其邻域中最高频率的值。 NoData 覆盖了右下角的两个位置,因为对于这两个位置来说,它是出现频率最高的值。

在下图中,收缩被应用于输入栅格,因此区域 4 和区域 6 将收缩一个像元。 在左上角,值 4 保留,因为它深于一个像元。
要在 Python 中指定多个区域值,请使用方括号定义多值列表。
参考资料
Matheron, G., Elements pour une Theorie del Milieux Poreux, Masson, Paris, 1967
Serra, J. Image Analysis and Mathematical Morphology, Academic Press, London 1982