需要 Geostatistical Analyst 许可。
要从数据中移除面趋势并去除趋势(残差)数据使用克里金法或协同克里金法,请考虑使用加法模型:
Z(s) = µ(s) + ε(s),其中,µ(s) 是某种确定性表面(趋势),ε(s) 是一种空间自相关误差。
从概念上讲,趋势是固定的,这意味着在您一次又一次对数据进行模拟时,趋势始终不变。 但是,由于存在自相关随机误差,您会看到模拟面中存在波动。 通常,趋势在整个空间中逐渐变化,而随机误差变化速度更快。 例如,在气象学上,您观测到(理论上已知)随纬度变化的温度梯度就是趋势。 不过,给定日期的观测值可能会因为锋面、地面覆被和云纹等原因而显现局部变化,这是不可预测的,所以在建模时会将局部变化作为自相关因素对待。
很不幸,没有一种理想方式能够以独特方式将数据分解成趋势和随机误差。 以下是实用指南。
在以下去除趋势图中,数据是通过两个模型进行模拟的。 一种模拟基于普通克里金法模型,其中 Z(s) = µ + ε(s) 和误差都是自相关的。 该过程中,对于指数半变异函数,平均值 µ = 0。 另一个数据集基于泛克里金模型进行模拟,表达式为 µ(s) = ß0 + ß1x(s) + ß2x2(s)(如下图中实线所示),但是误差是独立的(平均值为 0,方差为 1)。
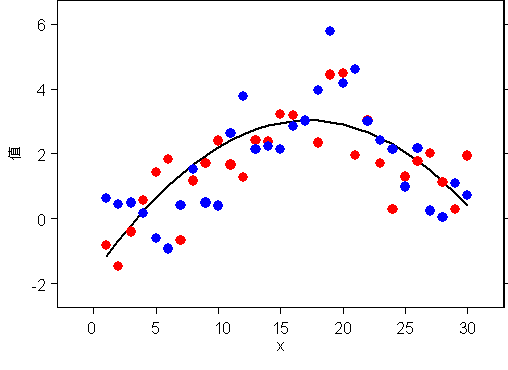
很难区分模型(蓝色圆圈来自普通克里金模型,红色圆圈来自具有独立误差的泛克里金模型)。 空间自相关支持灵活预测面,此示例表明很难仅根据数据确定合适的模型。 通常,需要使用普通克里金法,除非您有移除趋势面的合理理由。 原因是建议尽可能简化模型。 如果您移除趋势面,则需要估算更多参数。 对于二维二次表面,除了需要估算截距参数,还需要估算五个参数。 估计的参数越多,模型的准确度就越低。
但是,可能有时可通过空间坐标表示数据中的某一已知趋势。 例如,庄稼产量可能随纬度的变化而变化,这是因为温度、湿度、降雨量等也随着纬度的变化而变化,而不是因为坐标本身。 在此类情况下,建议去除趋势面。 再次注意,请保持表面尽可能简单,例如一阶多项式或二阶多项式。
如果使用趋势并且保留的残差变化过小以适当考虑预测的不确定性,则可能存在过度拟合数据的风险。 一定要通过交叉验证或在使用趋势模式时进行验证来检查模型。
还可以使用方向趋势工具沿不同方向可视化趋势,以帮助确定适当的趋势去除模型。 尝试不同的方向和多项式阶次,查看不同方向上的趋势变化情况。