通过成对比较分配权重工具通过成对比较输入变量,计算其相对权重。 为了确保所有变量对之间的比较评估在逻辑上保持一致,该工具提供了诊断功能。 该工具会计算一致性比率 (CR),帮助您提高评估结果的一致性。 例如,如果在成对比较中,您认为变量 A 比变量 B 重要两倍,变量 B 比变量 C 重要两倍,而变量 C 又与变量 A 同等重要,则评估结果在逻辑上不一致。 换言之,如果 A > B 且 B > C,则 C 不可能等于 A。
将 CR 控制在可接受的范围内有助于避免出现这种逻辑矛盾。 根据 Saaty (2000) 的观点:
- 如果 CR <= 0.1,则认为成对比较具有可接受的一致性。
- 如果 CR > 0.1,则应该调整比较评估,从而提高结果的一致性。
一致性比率的计算过程
计算 CR 的步骤如下:
- 计算一致性指标 (CI)。
- 根据变量的数量确定随机指标 (RI)。
- 通过将 CI 除以 RI 得到 CR。
以下示例将使用一个包含五个变量的比较矩阵,演示如何计算 CR。
| 变量 | Solar_Gain | 坡向 | 高程 | Dist_to_Road | Dist_to_Elect | 权重 |
|---|---|---|---|---|---|---|
Solar_Gain | 1 | 3 | 2 | 2 | 0.333 | 0.235 |
坡向 | 0.333 | 1 | 0.5 | 1 | 0.2 | 0.089 |
高程 | 0.5 | 2 | 1 | 1 | 0.5 | 0.136 |
Dist_to_Road | 0.5 | 1 | 1 | 1 | 5 | 0.247 |
Dist_to_Elect | 3 | 5 | 2 | 0.2 | 1 | 0.294 |
以下公式用于进行相关计算。
计算 CI
将使用以下公式计算 CI:

其中:
- λ(主特征值)是每个变量的 λi 值的平均值
- n 是输入变量的数量。
每个变量的 λi 值按以下公式计算:

其中:
- wi 表示每个输入变量的派生权重(即表 1 中“权重”列的值)。
- SWi 表示每个变量 i 的加权总和。
每个变量的加权总和按以下公式计算:
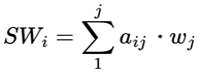
其中:
- aij 是原始成对比较矩阵中的数值,其中 i 表示行号,j 表示列号。
- wj 是对应变量的派生权重。
例如,变量 Solar_Gain 所在行的 SW 的计算方法如下:

变量 Solar_Gain 的 λi 值按以下公式计算:
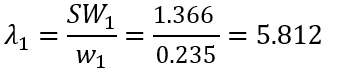
对每行重复上述计算,求出每个变量的 λi 值。
然后,对所有 λi 值求平均值,即可得到 λ。
在本例中,λ 的值为 6.462,如下表所示。
| 变量 | 权重(wi) | 加权总和(SWi) | λi = SWi / wi |
|---|---|---|---|
Solar_Gain | 0.235 | 1.366 | 5.812 |
坡向 | 0.089 | 0.541 | 6.079 |
高程 | 0.136 | 0.826 | 6.070 |
Dist_to_Road | 0.247 | 2.060 | 8.338 |
Dist_to_Elect | 0.294 | 1.765 | 6.005 |
平均值 | NA | NA | 6.462 |
计算出 λ 之后,即可使用上述公式计算 CI。
由于本示例中有五个变量,因此 CI 的计算公式如下:
CI = (6.462 - 5)/(5 - 1) = 0.365计算 RI
RI 是一个预定义的统计值,用于为成对比较的一致性比率计算提供基准。 由 Saaty (2000) 提出的 RI 值来源于对每个矩阵大小进行的蒙特卡洛模拟。 下表显示了每个矩阵大小对应的 RI 值。 矩阵大小在表格的顶行中标识。
| 矩阵大小 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
RI | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
当只有两个变量进行比较时,RI 值为 0,因为此时的比较本质上就是一致的。 RI 值会随着输入变量数量的增加而增大。
在本例中,变量的数量为 5,因此对应的 RI 值为 1.12。
计算 CR
通过将 CI 除以 RI 得到 CR。 CR 值可以衡量成对比较结果的一致性程度。
在本例中,CR 的计算公式如下:
CR = 0.365/1.12 = 0.326由于 CR 值大于 0.1,因此您应该修改比较评估,以提高结果的一致性。
提高一致性
如果确定输入变量的比较结果不一致,则会突出显示对不一致性影响最大的三个变量对。 应调整这些突出显示的变量对,从而提高结果的一致性。
以下工作流用于确定三个最不一致的变量对。
构建成对一致性矩阵
构建一个用于成对一致性评估的矩阵(Saaty, 2003)。 在以下公式中,此矩阵被称为 εij:

其中:
- aij 是原始成对比较矩阵中的数值,其中 i 表示行号,j 表示列号。
- wj 和 wi 分别是变量 j 和变量 i 的派生权重。
计算值
构建矩阵后,找出矩阵 εij 中的三个最大值。 这三个值对应的行和列所代表的变量对被认为是不一致的变量对。
在本比较示例中,CR 值为 0.326,大于 0.1。 为了确定不一致的变量对,Solar_Gain 所在行与 Aspect 所在列的交叉像元的 εij 值计算如下:
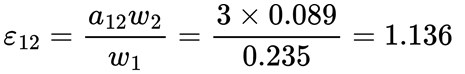
重复上述计算,求出所有像元的数值。
确定最不一致的变量对
上述比较示例的 εij 矩阵如下所示:

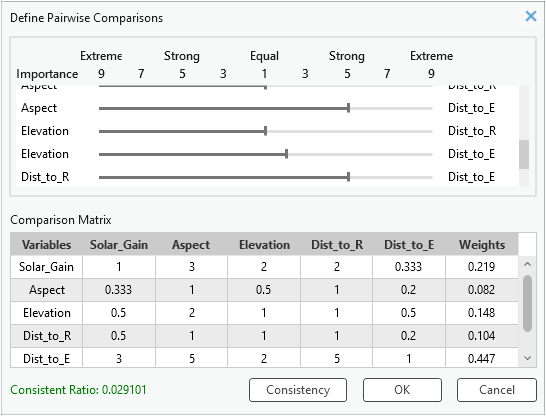
矩阵中数值最大的三个像元对应着对不一致性影响最大的比较。 它们分别是变量 Dist_to_Road 和 Dist_to_Elect、变量 Aspect 和 Dist_to_Road,以及变量 Dist_to_Elect 和 Solar_Gain 之间的比较评估。 在工具对话框中,滑块两侧会以红色突出显示这三个变量对。
在原始比较矩阵中,变量 Solar_Gain 的重要性被评估为变量 Dist_to_Road 的两倍 (Solar_Gain > Dist_to_Road),以及变量 Dist_to_Elect 的三分之一 (Dist_to_Elect > Solar_Gain)。 从逻辑上讲,Dist_to_Road 的重要性应该低于 Dist_to_Elect (Dist_to_Elect > Dist_to_Road)。 然而,在原始比较中,评估结果却错误地为 Dist_to_Road 分配了比 Dist_to_Elect 高五倍的权重 (Dist_to_Road > Dist_to_Elect)。 这是导致不一致的主要原因。
为了纠正这一问题,请将滑块向 Dist_to_Elect 侧移动,然后重新检查 CR 值。 例如,如果将滑块移动到 Dist_to_Elect 侧的位置 5,然后再次单击一致性按钮,则新的 CR 值为 0.029,这表明整体比较现在是一致的。
参考资料
Saaty, T. L. 2000. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. Pittsburgh, PA: RWS Publications
Saaty, T. L. 2003. "Decision-making with the AHP: Why is the principal eigenvector necessary". European Journal of Operational Research, 145(1), 85-91.