需要 Geostatistical Analyst 许可。
全局多项式插值法可将由数学函数(多项式)定义的平滑表面拟合到输入样本点。 全局多项式表面表面会逐渐变化,并捕捉数据中的粗尺度模式。
从概念上讲,全局多项式插值法就像拿一张纸并将其拟合到凸起的点之间(凸起到值的高度)。 下图展示了一组在缓坡山体上采集的高程样本点(纸张为洋红色)。

但一张平整的纸张无法精确呈现包含山谷的景观。 但是,如果允许将纸张弯曲,则将得到更加贴合的效果。 向数学公式中添加一项会产生类似结果,即平面弯曲。 平面(纸张没有弯曲)是一个一阶多项式(线性)。 允许一次弯曲是二阶多项式(二次),允许两次弯曲是三阶多项式(三次),依此类推;Geostatistical Analyst 中最多允许 10 次弯曲。 下图在概念上演示了拟合到山谷的二阶多项式。
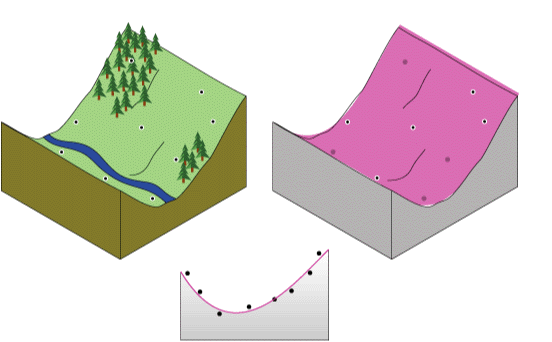
纸张很少会经过实际测量点,因此全局多项式插值法是一种不精确的插值器。 一些点将位于纸张上方,而其他点将位于纸张下方。 但是,如果将纸张上方每个点的高度相加,并将纸张下方每个点的高度相加,这两个总和应该相似。 通过使用最小二乘回归拟合获得洋红色表面。 所得到的表面可使凸起值与纸张之间的平方差达到最小化。
何时使用全局多项式插值法
全局多项式插值法的结果是一个平滑表面,其中呈现了感兴趣区域表面的渐进趋势。
全局多项式插值法用于以下情况:
- 当感兴趣区域的表面随区域缓慢变化时(例如工业区上空的污染分布),将表面拟合到采样点。
- 检查或排除长期趋势或全局趋势的影响。 此类情况下,采用的方法通常为趋势面分析。
全局多项式插值法将使用可能描述某些物理过程(例如污染和风向)的低阶多项式创建一个缓慢变化的表面。 但请注意,多项式越复杂,赋予其物理意义则越困难。 此外,计算表面极易受到异常值(极高值或极低值)的影响,尤其是位于边缘处。