以下是可创建随机值的各种工具的可用分布法。 分布法将从指定流(在分析环境中全局识别或在工具本地识别)创建的 0-1 随机值转换为指定的分布。 有关每种分布模式的语法及参数信息,请参阅随机值的分布语法。
均匀分布
均匀分布是一种连续概率分布,其中指定区间内的所有值具有相同的概率。 整数分布是离散版本的均匀分布(请参阅下文)。 在模拟模型中模拟气体浓度或交叉路口事故间隔时间时,以及在创建随机点工具中放置点时,可以使用均匀分布。
当每个潜在结果或事件发生的概率相等时,均匀分布通常用于对随机事件进行建模。

均匀分布的公式如下:

其中
a 是等概率间隔的最小值。
b 是等概率间隔的最大值。
x 是观测值。
所选的随机值介于最小值和最大值之间(不包括最大值和最小值)。 最小值必须小于最大值。 如果没有提供最小值和最大值,则会产生 0.0 和 1.0 之间的均匀变量。
整数分布
整数分布是一种概率分布,其中指定区间内的所有离散值具有相同的概率。 整数分布是离散版本的均匀分布(请参阅上文)。 整数分布可用于模拟投掷骰子时每个数字出现的概率(每个数字出现的概率为六分之一)、建模模拟模型中的随机事件或选择生物学研究的采样地点。
当每个潜在结果或事件发生的概率相等时,整数分布通常用于对随机事件进行建模。

整数分布的公式如下所示:

其中
a 是等概率间隔的最小值。
b 是等概率间隔的最大值。
x 是观测值。
所选的随机值介于最小值和最大值之间(不包括最大值和最小值)。 最小值必须小于最大值。 如果没有提供最小值和最大值,则会产生 1 和 100 之间的均匀值。
正态分布
正态分布模型是常见的连续随机变量。 正态分布应用广泛,适用于许多应用。 它建立在中心极限定理的基础上,该定理基于这样的原理:如果存在大量观测值,则随机变量的总和呈正态分布。 例如,如果硬币被抛很多次,那么在一系列抛硬币动作中正面出现的次数将趋近于正态。 正态分布的例子有:一个国家/地区中人的身高、一个州的高程值以及所有 12 岁学生的数学考试成绩。
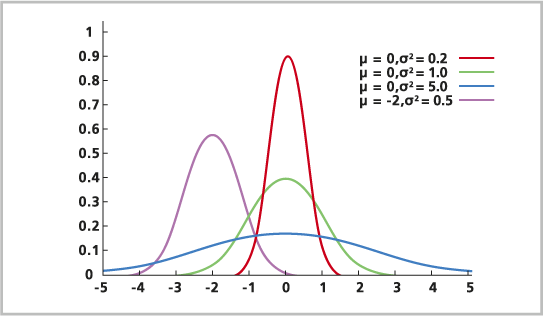
正态分布的公式如下:

其中
μ 是平均值。
σ 是标准差(正数)。
正态分布相对于平均值、众数和中位数对称,它们在 μ 处均相等。
通常,二项式和泊松分布使用相对较少的观测值来对未来离散、独立、随机、真实或虚假事件(例如,抛硬币时正面出现的次数)进行建模,而正态分布使用大量观测值来对连续变量(例如,身高、体重和金额)进行建模。 二项式和泊松分布基于概率,而正态分布是满足数量或幅度的观测值的数量。
指数分布
指数分布是连续的概率分布。 它通常用于模拟以恒定平均速率发生的事件之间的时间,或者可以使用分布来模拟每单位距离内事件的发生。 十字路口发生下一次车祸的时间、夜空中看到两颗流星之间的时间以及街道上坑洼之间的距离都是可以使用指数分布的例子。 对于每一个例子,随着时间或距离的增加,状态改变或事件发生的可能性呈指数级增长。 事件的发生是彼此独立的。
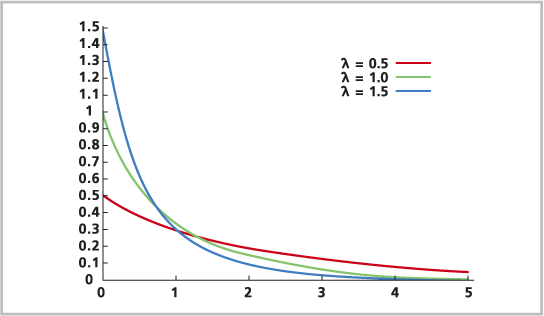
指数分布的公式如下:
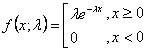
其中
e 是自然对数。
x 是事件可能发生的次数(正整数值)。
指数分布模型泊松过程,其中现象处于初始状态。 指数分布是连续版本的几何分布。 如果从状态 A 转移到状态 B 的过程可以分解为几个独立的任务,那么用 Gamma 分布对其进行建模可能会更好。 Gamma 分布模拟多个独立的、指数分布的变量的总和。 它可以被视为指数分布的一个特例。
泊松分布
泊松分布是一种离散概率分布。 泊松分布模拟在已知平均值的情况下,在固定时间步长内发生事件次数的概率。 事件与上次发生的时间无关。 x 轴是事件 0、1、2、3、4 等的离散值(通常表示事件发生的次数),y 轴是已知平均值的情况下该现象发生次数的概率。 这些事件可以是十字路口发生的事故数量、出生缺陷的数量或每平方公里内驼鹿的数量。 泊松分布模型代表罕见事件。 这种分布有时被称为小数定律,因为这种事件并不经常发生,但发生的机会却有很多。
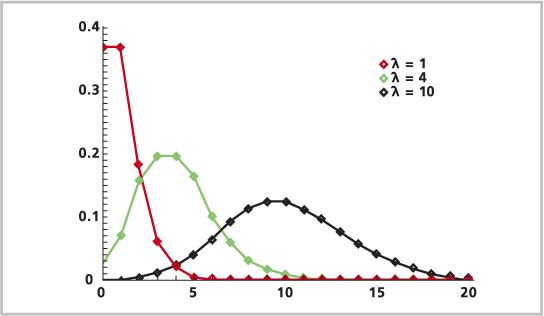
公式如下所示:
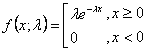
其中
e 是自然对数。
k 是事件可能发生的次数(正整数值)。
k! 是 k 的阶乘。
λ(或平均值)是正数,表示指定间隔内发生的预期次数。 如果事件在一小时(60 分钟)内每 10 分钟发生一次,则 lambda 为 6。
泊松分布与二项分布相似;然而,泊松分布在不知道可能发生事件总数信息的情况下对罕见事件的发生进行建模。 泊松分布考察的是十字路口的事故数量,而二项分布则模拟的是相对于通过十字路口的汽车数量的事故数量。
Gamma 分布
Gamma 分布是连续的概率分布。 Gamma 分布模拟多个独立的、指数分布的变量的总和。 它可以被视为指数分布的一个特例。
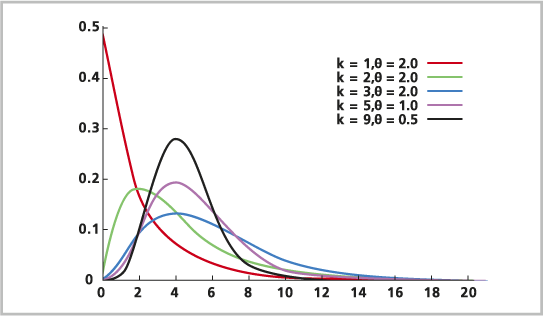
Gamma 分布的公式如下:
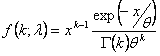
参数化 Gamma 分布的另一种方法如下所示:
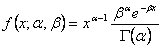
对于 alpha 为 1 的情况,Gamma 分布等于指数分布。 当 alpha 为整数时,gamma 分布变为 Erlang 分布。 对于整数 alpha 和等于 2 的 beta,gamma 分布变为具有 2 个 alpha 自由度的卡方分布。
结果变量大于或等于 0.0。 alpha 和 beta 必须大于 0.0。
二项分布
二项分布在观测事件的潜在创建者序列时对事件发生的次数进行建模。 例如,二项分布可以记录临床研究中死于心脏病的人数、拥挤电梯中从二楼出来的人数、或种群中携带某种遗传特征的动物的数量。

二项分布描述的是发生的情况,而不是量级。 它可能模拟有多少参赛者完成了比赛,而不是参赛者的速度有多快。
二项分布的公式如下:
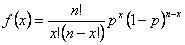
其中
n 是观测值个数。
p 是发生的概率。
x 是成功次数,范围从 0 到 n。
二项分布的一个常见用途是确定抛硬币 10 次(n = 10)时出现正面的次数的概率。 10 次中可能没有一次正面,10 次中可能只有 1 次正面,依此类推;因此,x = 0、1、2、3、4、5、6、7、8、9、10。 p 是每个 x 的概率。
所有试验都是独立的,每次试验都有成功或失败的结果。
当 n 较大且 p 较小时,二项分布接近泊松分布。 在这种情况下,使用泊松分布可能会更容易。
二项分布返回 n 次试验中成功次数的随机变量,其中每次试验的成功概率为 p(例如,正面朝上的概率为 p)。
几何分布
几何分布是一种离散概率分布。 它模拟的现象主要有两种:(1) 成功所需次数的概率(例如,掷出数字 6 所需的掷骰子次数)或 (2) 成功之前失败次数的概率(例如,在看到鹿之前在小路上徒步的次数)。 第一次徒步行走时没有看到鹿的概率是 (1 - p)。 对于第二次徒步旅行,没有看到鹿的概率是 (1 - p) (1 - p)。 随着在路上徒步的次数增多,看不到鹿的概率会逐渐降低,最终总会看到一只鹿。 这些事件彼此独立。

几何分布的公式如下:

其中
p 是成功的概率。
n 是试验次数。
几何分布是离散版本的指数分布(请参阅上文)。 几何分布是负二项分布或帕斯卡分布的一个特例,帕斯卡分布中的 r 等于 1(见下文)。
负二项分布
负二项分布是一种离散概率分布。 负二项分布基于伯努利试验。 伯努利试验模型事件:试验结果有两种(成功或失败)之一;成功的概率为 p(每次试验的 p 相同);并且彼此独立。 抛硬币就是伯努利试验。 例如,负二项分布可以模拟连续五次抛硬币出现正面的情况需要抛多少次。 因此,负二项分布模拟了成功之前的失败次数。 当 r 为整数时,负二项式就成为一种特殊情况,称为帕斯卡分布。
负二项分布的公式如下:

其中
r 是失败次数。
p 是成功的概率。
k 是成功次数,范围从 0 到 n。
当负二项分布代表抛硬币时,将返回一个随机值,表示出现正面所需的次数。