需要 Spatial Analyst 许可。
波段集统计工具为一组栅格波段的多元分析提供统计数据。 当启用计算协方差和相关矩阵选项时,将输出协方差和相关矩阵,以及基本统计参数,例如每个图层的最小值、最大值、平均值和标准差值。 如果启用计算直方图选项,则将计算直方图统计数据并将其添加至输出统计数据文件。 如果指定输出直方图表,则将创建包含直方图信息的输出表。 如果指定输出直方图名称,则将创建直方图并将其添加至内容列表。
协方差矩阵包含方差和协方差的值。 方差是一种统计测量值,显示与均值之间的方差大小。 为了计算这些方差,对每个像元值与所有像元的平均值之间的差值的平方进行平均。 可以沿着协方差矩阵的对角线从左上角到右下角读取各图层的方差。 方差以像元值单位的平方表示。
协方差矩阵中的其余条目是所有输入栅格对之间的协方差。 下面的公式用于确定图层 i 和 j 之间的协方差:
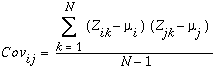
其中:
Z - 像元的值
i, j - 为堆叠的图层
µ - 为一个图层的平均值
N - 为像元数量
k - 表示特定像元
两个图层的协方差是相应行和列的交集。 图层 2 和图层 3 之间的协方差与图层 3 和图层 2 之间的协方差相同。 协方差矩阵的值取决于值单位,而相关矩阵的值则不是。
相关矩阵显示了描述两个数据集之间关系的相关系数的值。 对于一组栅格图层,相关矩阵表示来自一个栅格图层的像元值与另一图层的像元值的关系。 两个图层之间的相关性是图层之间依赖关系的度量。 它是两个图层之间的协方差除以它们的标准差的乘积的比率。 因为它是一个比率,所以它是一个无单位的数字。 计算相关性的公式如下:

相关性范围从 +1 到 -1。 正相关表示两个图层之间存在直接关系,例如当一个图层的像元值增加时,另一个图层的像元值也有可能增加。 负相关表示一个变量与另一个变量的变化相反。 相关性为零表示两个图层相互独立。
相关矩阵是对称的。 它从左上角到右下角的对角线为 1.0000,因为相同图层的相关系数为 +1。
输出统计数据文件示例
输出统计数据文件支持两种输出格式:逗号分隔值 (CSV) 格式或 Markdown 格式。 以下是四波段输入栅格的上述格式的输出统计数据文件示例。
CSV 输出
当指定输出统计数据文件为文本文件(文件扩展名为 .txt、.csv 或 .asc)时,将使用逗号分隔值 (CSV) 格式保存该文件,由此可将其导入其他软件(如 Excel)以进行进一步分析或可视化。
以下是在禁用计算协方差和相关矩阵选项和计算直方图选项的情况下创建的文本文件的内容。 输入图层的源数据路径将在文件顶部列出。
Output Band Collection Statistics Input Layers Layer,Path Layer_1,C:\example\mb_data.tif\Band_1 Layer_2,C:\example\mb_data.tif\Band_2 Layer_3,C:\example\mb_data.tif\Band_3 Layer_4,C:\example\mb_data.tif\Band_4 Statistics of Individual Layers Layer,Min,Max,Mean,Std. Dev. 1,48.00000,255.00000,73.70110,11.90945 2,22.00000,255.00000,33.73108,7.49241 3,17.00000,255.00000,31.77404,11.40892 4,13.00000,255.00000,82.51136,17.67144
Markdown 输出
如果指定文件扩展名为 .md,则将使用 Markdown 格式保存输出统计数据文件。
当以纯文本文件形式查看时,以下是在启用计算协方差和相关矩阵选项并禁用计算直方图选项的情况下创建的 Markdown 文件的内容。
# Output Band Collection Statistics ### Input Layers | Layer | Path | | ------: | ----------------------------: | | Layer_1 | C:\example\mb_data.tif\Band_1 | | Layer_2 | C:\example\mb_data.tif\Band_2 | | Layer_3 | C:\example\mb_data.tif\Band_3 | | Layer_4 | C:\example\mb_data.tif\Band_4 | ### Statistics of Individual Layers | Layer | Min | Max | Mean | Std. Dev. | | ----: | -------: | --------: | -------: | --------: | | 1 | 48.00000 | 255.00000 | 73.70110 | 11.90945 | | 2 | 22.00000 | 255.00000 | 33.73108 | 7.49241 | | 3 | 17.00000 | 255.00000 | 31.77404 | 11.40892 | | 4 | 13.00000 | 255.00000 | 82.51136 | 17.67144 | ### Covariance Matrix | Layer | 1 | 2 | 3 | 4 | | ----: | --------: | --------: | --------: | --------: | | 1 | 141.83498 | 86.72548 | 131.13040 | -54.33298 | | 2 | 86.72548 | 56.13628 | 84.01048 | -24.88371 | | 3 | 131.13040 | 84.01048 | 130.16340 | -53.35075 | | 4 | -54.33298 | -24.88371 | -53.35075 | 312.27971 | ### Correlation Matrix | Layer | 1 | 2 | 3 | 4 | | ----: | -------: | -------: | -------: | -------: | | 1 | 1.00000 | 0.97193 | 0.96509 | -0.25817 | | 2 | 0.97193 | 1.00000 | 0.98280 | -0.18794 | | 3 | 0.96509 | 0.98280 | 1.00000 | -0.26462 | | 4 | -0.25817 | -0.18794 | -0.26462 | 1.00000 |
渲染后的 Markdown 输出
以下是渲染后 Markdown 格式的输出文件的示例。 将在启用计算直方图选项并禁用计算协方差和相关矩阵选项的情况下创建此输出文件。

其他资源
有关详细信息,请参阅以下内容:
Snedecor, G. W., and W. G. Cochran. 1968. Statistical Methods, 6th ed. Ames, Iowa: The Iowa State University Press.