The Density-based Clustering tool works by detecting areas where points are concentrated and where they are separated by areas that are empty or sparse. Points that are not part of a cluster are labeled as noise. Optionally, the time of the points can be used to find groups of points that cluster together in space and time.
This tool uses unsupervised machine learning clustering algorithms that automatically detect patterns based purely on spatial location and the distance to a specified number of neighbors. These algorithms are considered unsupervised because they do not require any training on what it means to be a cluster.
Tip:
Clustering, grouping, and classification techniques are some of the most widely used methods in machine learning. The Multivariate Clustering and Spatially Constrained Multivariate Clustering tools also use unsupervised machine learning methods to determine natural clusters in data. These classification methods are considered unsupervised, as they do not require a set of preclassified features to guide or train on to find clusters in data.
Potential applications
Some of the ways this tool can be applied are as follows:
- Urban water supply networks are an important hidden underground asset. The clustering of pipe ruptures and bursting can indicate looming problems. Using the Density-based Clustering tool, an engineer can find where these clusters are and take preemptive action on high-danger zones within water supply networks.
- Suppose you have position data for all successful and unsuccessful shots for NBA players. The Density-based Clustering tool can show you the different patterns of successful versus failed shot positions for each player. This information can then be used to inform game strategy.
- Say you are studying a particular pest-borne disease and have a point dataset representing households in your study area, some of which are infested, some of which are not. By using the Density-based Clustering tool, you can determine the largest clusters of infested households to help pinpoint an area to begin treatment and extermination of pests.
- Geolocating tweets following natural hazards or terror attacks can be clustered, and rescue and evacuation needs can be informed based on the size and location of the clusters identified.
Clustering Methods
The Density-based Clustering tool's Clustering Methods parameter provides three options with which to find clusters in point data:
- Defined distance (DBSCAN)—Uses a specified distance to separate dense clusters from sparser noise. The DBSCAN algorithm is the fastest of the clustering methods, but is only appropriate if there is a very clear search distance to use, and that works well for all potential clusters. This requires that all meaningful clusters have similar densities. This method also allows you to use the Time Field and Search Time Interval parameters to find clusters of points in space and time.
- Self-adjusting (HDBSCAN)—Uses a range of distances to separate clusters of varying densities from sparser noise. The HDBSCAN algorithm is the most data-driven of the clustering methods, and thus requires the least user input.
- Multi-scale (OPTICS)—Uses the distance between neighboring features to create a reachability plot, which is then used to separate clusters of varying densities from noise. The OPTICS algorithm offers the most flexibility in fine-tuning the clusters that are detected, though it is computationally intensive, particularly with a large search distance. This method also allows you to use the Time Field and Search Time Interval parameters to find clusters of points in space and time.
This tool requires a value representing the minimum number of features required to be considered a cluster. Depending on the selected clustering method, there may be additional parameters to specify, as described below.
Minimum Features per Cluster
This parameter determines the minimum number of features required to consider a grouping of points a cluster. For instance, if you have a number of different clusters, ranging in size from 10 points to 100 points, and you choose a Minimum Features per Cluster parameter value equal to 20, all clusters that have less than 20 points will either be considered noise (because they do not form a grouping large enough to be considered a cluster) or they will be merged with nearby clusters to satisfy the minimum number of features required. In contrast, choosing a Minimum Features per Cluster parameter value smaller than what you consider your smallest meaningful cluster may lead to subdivision of the clusters. In other words, the smaller the Minimum Features per Cluster parameter value, the more clusters will be detected. The larger the value, the fewer clusters will be detected.
Tip:
The ideal Minimum Features per Cluster parameter value depends on what you are trying to capture and your analysis question. It should be set to the smallest size grouping you want to consider a meaningful cluster. Increasing the value may result in merging some of the smaller clusters.
The Minimum Features per Cluster parameter is also important in the calculation of the core-distance, which is a measurement used by all three methods to find clusters. Conceptually, the core-distance for each point is a measurement of the distance that is required to travel from each point to the defined minimum number of features. So, if a large minimum features per cluster is chosen, the corresponding core-distance will be larger. If a small value is chosen, the corresponding core-distance will be smaller. The core-distance is related to the Search Distance parameter, which is used by both the Defined distance (DBSCAN) and Multi-scale (OPTICS) clustering methods.
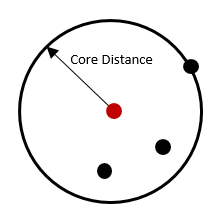
Search Distance (DBSCAN and OPTICS)
For Defined distance (DBSCAN), if the Minimum Features per Cluster parameter value can be found within the search distance from a particular point, that point will be marked as a core-point and included in a cluster, along with all points within the core-distance. A border-point is a point that is within the search distance of a core-point but does not itself have the minimum number of features within the search distance. Each resulting cluster is composed of core-points and border-points, where core-points tend to fall in the middle of the cluster and border-points fall on the exterior. If a point does not have the minimum number of features within the search distance and is not within the search distance of another core-point (in other words, it is neither a core-point nor a border-point), it is marked as a noise point and not included in any cluster.
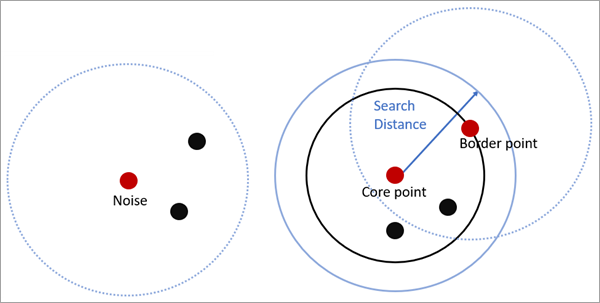
For the Multi-scale (OPTICS) clustering method, the search distance value is treated as the maximum distance that will be compared to the core-distance. Multi-scale (OPTICS) uses a concept of a minimum reachability distance, which is the distance from a point to its nearest neighbor that has not yet been visited by the search. (Note: OPTICS is an ordered algorithm that starts with the feature with the smallest ID and goes from that point to the next to create a plot. The order of the points is fundamental to the results.) Multi-scale (OPTICS) will search all neighbor distances within the specified search distance, comparing each of them to the core-distance. If any distance is smaller than the core-distance, that feature is assigned that core-distance as its reachability distance. If all of the distances are larger than the core-distance, the smallest of those distances is assigned as the reachability distance. When no further points are inside the search distance, the process restarts at a new point that has not previously been visited. At each iteration, reachability distances are recalculated and sorted. The smallest of the distances is used for the final reachability distance of each point. These reachability distances are then used to create the reachability plot, which is an ordered plot of the reachability distances that is used to detect clusters.
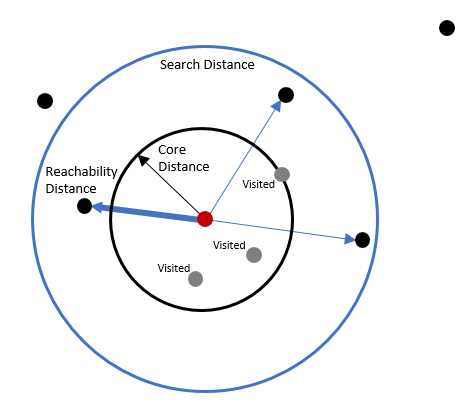
For both Defined distance (DBSCAN) and Multi-scale (OPTICS), if no distance is specified, the default search distance is the highest core-distance found in the dataset, excluding those core-distances in the top 1 percent (in other words, excluding the most extreme core-distances).
Clustering in space and time (DBSCAN and OPTICS)
In two of the clustering methods, the time of each point can be provided in the Time Field parameter. If provided, the tool will find clusters of points that are close to each other in space and time. The Search Time Interval parameter is analogous to the search distance and is used to determine the core-points, border-points, and noise points of the space-time clusters.
For Defined distance (DBSCAN), when searching for cluster members, the minimum features per cluster must be found within the search distance and search time interval to be a core-point of a space-time cluster.
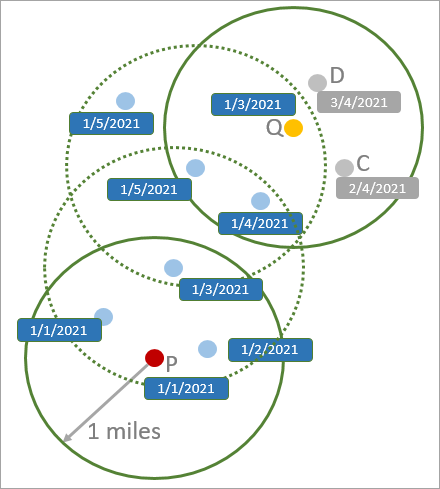
In the following image, the search distance is 1 mile, the search time interval is 3 days, and the minimum number of features is 4. The point P is a core point because there are four points within the search distance and time interval (including itself). The point Q is a border point because there are only three points within the search distance and time interval, but the point is within the search distance and time interval of a core-point of the cluster (the point with time stamp 1/5/2021). The points C and D are noise points because they are neither core-points nor border-points of the cluster, and all other points (including P and Q) form into a single cluster.
For Multi-scale (OPTICS), all points outside of the search time interval range of a point will be excluded when the point calculates its core-distance, searches all neighbor distances within the specified search distance, and calculates the reachability distance.
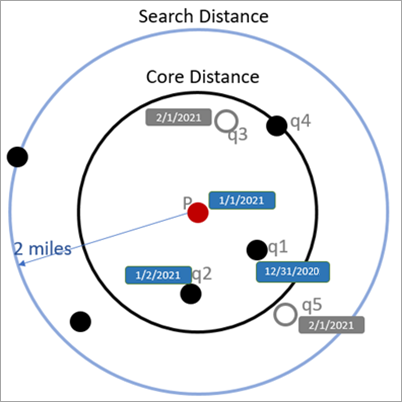
In the following image, the search distance is 2 miles, the search time interval is 3 days, and the minimum number of features is 4. The core-distance for point P is calculated skipping point q3 because it is outside of the search time interval. In this case, the core-distance of P is equal to the reachability distance of P.
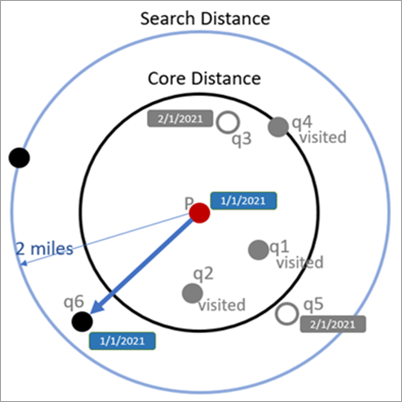
The next image shows the calculation of the reachability distance when some neighboring points have already been visited. Points q1, q2, and q4 were skipped because they were previously visited, and points q3 and q5 were skipped because they are outside of the search time window.
Reachability plot (OPTICS)
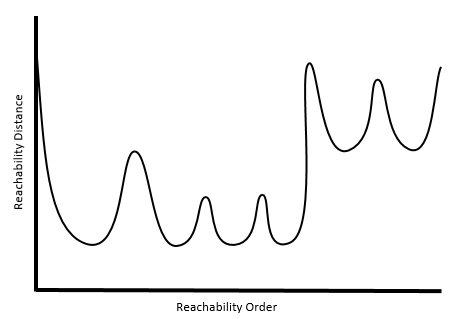
After all of the reachability distances have been calculated for the entire dataset, a reachability plot is constructed that orders the distances and reveals the clustering structure of the points.
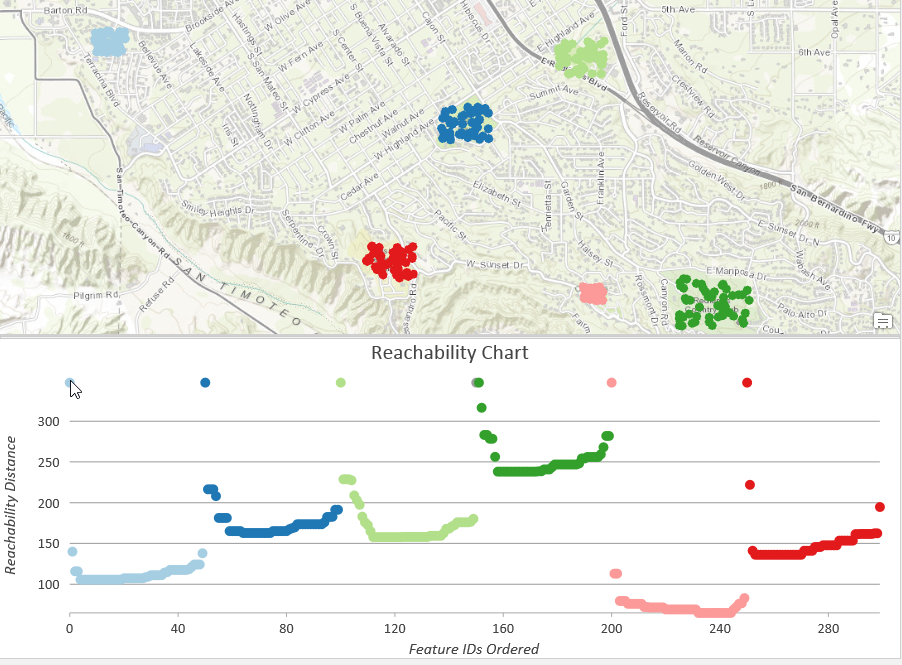
The valleys in the reachability plot imply that a short distance needs to be traveled from one point to the next. Thus, valleys represent distinct clusters in the point pattern. The denser a cluster, the lower the reachability distances will be, and the lower the valley on the plot (the pink cluster, for instance, is the most dense in the above example). Less dense clusters have higher reachability distances and higher valleys on the plot (the dark green cluster, for instance, is the least dense in the above example). The peaks represent the distances needed to travel from cluster to cluster, or from cluster to noise to cluster again, depending on the configuration of the set of points.
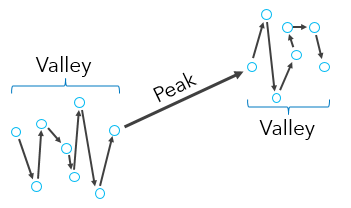
Plateaus can occur in a reachability plot when the search distance is less than the largest core-distance. A key aspect of using the OPTICS clustering method is determining how to detect clusters from the reachability plot, which is done using the Cluster Sensitivity parameter.
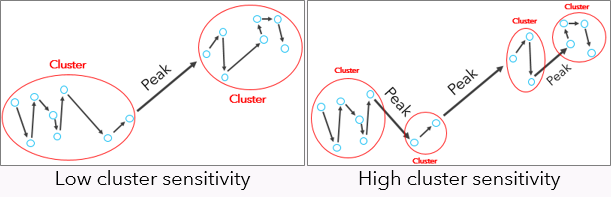
Cluster Sensitivity (OPTICS)
The Cluster Sensitivity parameter determines how the shape (both slope and height) of peaks within the reachability plot will be used to separate clusters. A very high Cluster Sensitivity (close to 100) will treat even the smallest peak as a separation between clusters, resulting in a higher number of clusters. A very low cluster sensitivity (close to 0) will treat only the steepest, highest peaks as a separation between clusters, resulting in a lower number of clusters.
The default cluster sensitivity is calculated as the threshold at which adding more clusters does not add more information, using the Kullback-Leibler Divergence between the original reachability plot and the smoothed reachability plot obtained after clustering.
Comparing the methods
While only Multi-scale (OPTICS) uses the reachability plot to detect clusters, the plot can be used to help explain, conceptually, how these methods differ. For the purposes of illustration, the reachability plot below will be used to explain the differences in the three methods. The plot reveals clusters of varying densities and separation distances. We'll explore the results of using each of the clustering methods on this illustrative data.
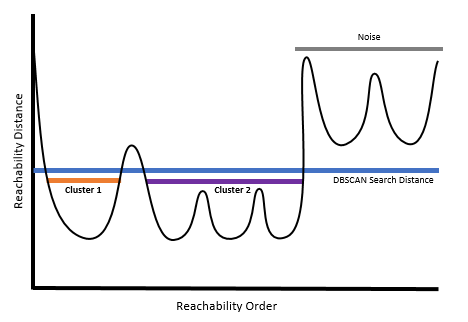
For Defined distance (DBSCAN), you can imagine drawing a line across the reachability plot at the specified search distance. Areas below the search distance represent clusters while peaks above the search distance represent noise points. Defined distance (DBSCAN) is the fastest of the clustering methods, but is only appropriate if there is a clear search distance to use as a cutoff, and that search distance works well for all clusters. This requires that all meaningful clusters have similar densities.
For Self-adjusting (HDBSCAN), the reachability distances can be thought of as nested levels of clusters. Each level of clustering would result in a different set of clusters being detected. Self-adjusting (HDBSCAN) chooses which level of clusters within each series of nested clusters will optimally create the most stable clusters that incorporate as many members as possible without incorporating noise. To learn more about the algorithm, refer to the documentation from the creators of HDBSCAN. Self-adjusting (HDBSCAN) is the most data-driven of the clustering methods, and thus requires the least user input.
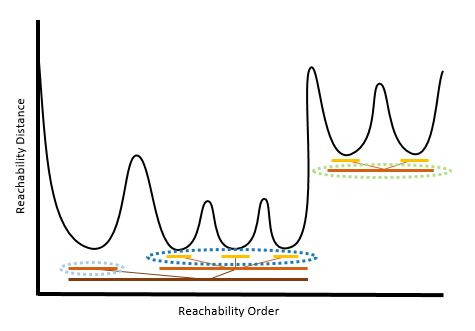
For Multi-scale (OPTICS), the work of detecting clusters is based not on a particular distance, but instead on the peaks and valleys within the plot. Let's say that each peak has a level of either Small, Medium, or Large.
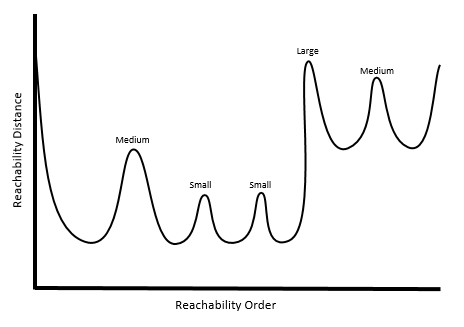
Choosing a very high Cluster Sensitivity essentially means that all peaks, from Small to Large, will act as separations between clusters (resulting in more clusters).
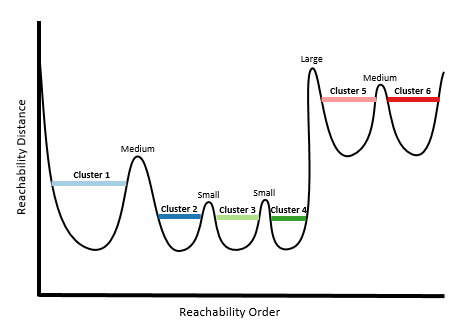
Choosing a moderate cluster sensitivity will result in both the Medium and Large peaks being used, but not the Small peaks.
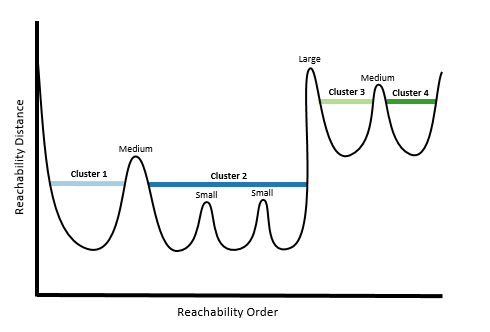
Choosing a very low cluster sensitivity will result in only the Large peaks being used, resulting in the lowest number of clusters detected.
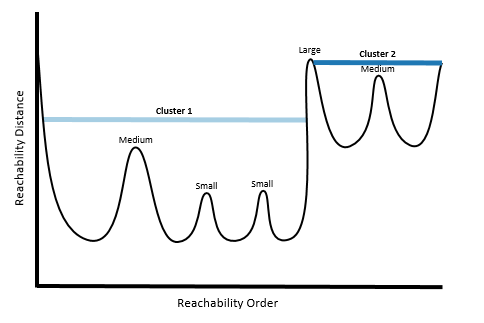
Multi-scale (OPTICS) provides the most flexibility in fine-tuning the clusters that are detected, though it is also the slowest of the three clustering methods.
Results
This tool produces an output feature class with a new integer field, CLUSTER_ID, showing you which cluster each feature is a member of. Default rendering is based on the COLOR_ID field. Multiple clusters will be assigned each color. Colors will be assigned and repeated so that each cluster is visually distinct from its neighboring clusters.
If Self-adjusting (HDBSCAN) is chosen for the Clustering Method parameter, the output feature class will also contain the fields PROB, which is the probability the feature belongs in its assigned group, OUTLIER, designating the feature may be an outlier within its own cluster (a higher value means the feature is more likely to be an outlier), and EXEMPLAR, which denotes the features that are the most representative of each cluster.
Note:
All points determined to be noise are considered part of the same cluster, and outliers, probabilities, and an exemplar are calculated for the noise cluster. These values may not be as meaningful as those calculated for other clusters that are not made of noise points.
This tool also creates messages and charts to help you understand the characteristics of the clusters identified. You can access the messages by hovering over the progress bar, clicking the pop-out button, and expanding the messages section in the Geoprocessing pane. You can also access the messages for a previous run of the Density-based Clustering tool using the geoprocessing history. The charts created can be accessed from the Contents pane.
In addition to the reachability plot that is created when Multi-scale (OPTICS) is chosen, all clustering methods will also create a Bar Chart that shows all unique Cluster IDs. This chart can be used to select all of the features that fall within a specified cluster, and to explore the size of each of the clusters.
Additional resources
For more information about DBSCAN, refer to the following:
- Birant, D. & Kut, A. (2007, January). "ST-DBSCAN: An algorithm for clustering spatial–temporal data." In Data & Knowledge Engineering (Vol 60, No. 1, pp. 208-221). https://doi.org/10.1016/j.datak.2006.01.013
- Ester, M., Kriegel, H. P., Sander, J., & Xu, X. (1996, August). "A density-based algorithm for discovering clusters in large spatial databases with noise." In Kdd (Vol. 96, No. 34, pp. 226-231).
For more information about HDBSCAN, refer to the following:
- Campello, R. J., Moulavi, D., & Sander, J. (2013, April). "Density-based clustering based on hierarchical density estimates." In Pacific-Asia Conference on Knowledge Discovery and Data Mining (pp. 160-172). Springer, Berlin, Heidelberg.
For more information about OPTICS, refer to the following:
- Agrawal, K. P., Garg, S., Sharma, S., & Patel, P. (2016, November). "Development and validation of OPTICS based spatio-temporal clustering technique." In Information Sciences (Vol 369, pp. 388-401). https://doi.org/10.1016/j.ins.2016.06.048.
- Ankerst, M., Breunig, M. M., Kriegel, H. P., & Sander, J. (1999, June). "OPTICS: ordering points to identify the clustering structure." In ACM Sigmod record (Vol. 28, No. 2, pp. 49-60). ACM.