Many tools and methods in the Spatial Statistics toolbox require defining spatial relationships between features. This entails identifying which features are considered neighbors of each other and how much influence neighbors should have on each other. This structure, defined through the combination of a neighborhood type and a weighting scheme, forms the foundation of many spatial analyses.
Spatial relationships
An important difference between spatial and traditional statistics is that spatial statistics integrates spatial relationships directly into their mathematics and models. Consequently, various tools have a Conceptualization of Spatial Relationships, Neighborhood Type, or Spatial Constraint parameter that allows you to define the spatial relationships between features.
Different spatial relationships emphasize different aspects of spatial structure. For example, in a housing market study, it might make sense to define each home's neighborhood as the few closest properties, weighted by distance, under the assumption that nearby sales exert the strongest influence. Other situations may require broader or more complex definitions, such as relating cities based on the number of travelers between them (where cities that are geographically far apart might still highly economically dependent). These choices affect everything from the detection of spatial patterns to the behavior of spatial models, so it is important to think about which spatial relationships are most appropriate for your data and questions.
When performing a spatial statistical analysis such as hot spot analysis or cluster and outlier analysis, you can define the spatial relationships directly in the tools using the tool parameters. However, you can also create a spatial weights matrix file (.swm) to store the neighbors and weights so that they can be reused in various tools.
Different tools and methods have various options for defining spatial relationships. While no single tool supports all possible relationships, the Generate Spatial Weights Matrix tool allows the widest variety of spatial relationships, and the output file can then be used and reused in other analysis tools. For all but the simplest spatial relationships, it is recommended to first define the spatial relationships in a spatial weights matrix file and then use the file in spatial analysis tools.
The various spatial relationships supported across the tools are described in the following sections:
Inverse distance
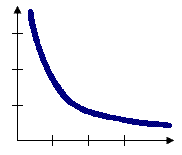
The inverse distance spatial relationship is one of impedance, or distance decay, in which the weight of neighboring features decreases by dividing by the distance between the neighbor and the focal feature. All features impact or influence all other features, but the farther away something is, the smaller the impact it has. This inverse distance is also commonly taken to a power, such as inverse distance squared, which causes the weight to decrease even faster. It is generally recommended to use a threshold distance with inverse distance relationships to reduce the number of neighbors with weights very close to 0. When threshold distance is specified, a default threshold value is computed for you, but you can force all features to be a neighbor of all other features by setting the threshold distance to 0.
Fixed distance band
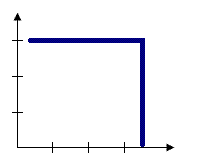
The fixed distance band spatial relationship imposes a sphere of influence around each feature, and all features within a given threshold distance around the focal feature will be included as neighbors. This option is appropriate when you want to evaluate the statistical properties of your data at a particular (fixed) spatial scale. If you are studying commuting patterns and know that the average journey to work is 15 miles, for example, you may want to use a 15 mile fixed distance for your analysis. See Best practices for selecting a fixed distance band value for strategies that can help you identify an appropriate scale of analysis.
Zone of indifference
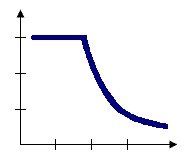
The zone of indifference spatial relationship combines the fixed distance band and inverse distance spatial relationships. Features within the threshold distance are included in analyses for the target feature. Once the threshold distance is exceeded, the level of influence (the weighting) quickly drops off. This method is appropriate when you want to hold the scale of analysis fixed but don't want to impose sharp boundaries on the neighboring features included in target feature computations.
Polygon contiguity
For polygon feature classes, you can choose to define neighbors using all polygons that are contiguous to the focal polygon. You can also choose whether to include polygons as neighbors if they only share a corner (called queen contiguity) or only include neighbors that share an edge (called rook contiguity). In various tools, these options are called Contiguity edges corners and Contiguity edges only, respectively. If any portion of two polygons overlap, they will be considered neighbors by both contiguity options.
Polygon contiguity can also be extended to higher orders, in which the order is the number of steps it would take to move from the focal polygon to its neighbors. First-order contiguity means that only the immediate neighbors of the focal polygon will be neighbors (those that can be reached in a single step). Order two means all polygons that can be reached in two steps or fewer (the first-order neighbors and all of their first-order neighbors) will be included as neighbors. If the polygons are arranged in a grid, higher orders will form concentric rings around the focal polygon. It is generally recommended to avoid using polygon orders larger than 3. You can create higher-order contiguity spatial relationships using the Generate Spatial Weights Matrix tool.
K nearest neighbors
The k nearest neighbors spatial relationship uses a specified number of its closest k features as neighbors, in which k is provided in the Number of Neighbors parameter. In locations where feature density is high, the spatial scale of the analysis will be smaller. Similarly, in locations where feature density is sparse, the spatial scale for the analysis will be larger. An advantage to this model of spatial relationships is that it ensures there will be some neighbors for every target feature, even when feature densities vary widely across the study area.
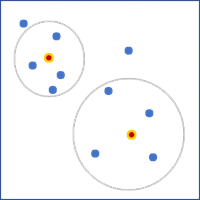
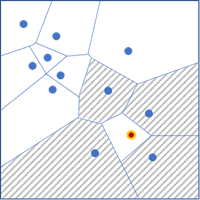
Delaunay triangulation
The Delaunay triangulation spatial relationship constructs neighbors by creating Voronoi triangles from point features or from feature centroids such that each point or centroid is a triangle node. Nodes connected by a triangle edge are considered neighbors. Using Delaunay triangulation ensures every feature will have at least one neighbor even when data includes islands or widely varying feature densities. Do not use the Delaunay Triangulation option when you have coincident features.
Space-Time window
With this option, you define feature relationships in terms of both a space (fixed distance) and a time (fixed-time interval) window. This option is available when you create a spatial weights matrix file using the Generate Spatial Weights Matrix tool. When you select the Space time window option, you are required to specify Date/Time Field, Date/Time Interval Type (hours, days, or months, for example), and Date/Time Interval Value parameter values. The interval value is an integer. If you selected the Hours option for the interval type and 3 for the interval value, for example, two features would be considered neighbors if the values in their Date/Time field are within three hours of each other. With this conceptualization, features are neighbors if they are within the specified distance and within the specified time interval of the target feature. As one possible example, you would select the Space time window option for the Conceptualization of Spatial Relationships parameter if you wanted to create a spatial weights matrix file to use with Hot Spot Analysis tool to identify space-time hot spots. Additional information, including how to visualize results, is presented in Space-Time Analysis. Other opportunities are available to help you visualize, in 3D, a netCDF space-time cube.
Get spatial weights from file
If your spatial relationships are defined in a spatial weights matrix (.swm) file, use this option to provide the file and apply the custom weights to the analysis. You can create these files using the Generate Spatial Weights Matrix tool, Generate Network Spatial Weights tool, Neighborhood Explorer, or various tools in the Spatial Component Utilities (Moran Eigenvectors) toolset.
Best practices for selecting spatial relationships
The more realistically you can model how features interact with each other in space, the more accurate your results will be. Your choice for the spatial relationships should reflect inherent relationships among the features you are analyzing. Sometimes your choice will also be influenced by characteristics of your data.
The inverse distance methods, for example, are most appropriate with continuous data or to model processes where the closer two features are in space, the more likely they are to interact with or influence each other. With this spatial relationship, every feature is potentially a neighbor of every other feature, and with large datasets, the number of computations involved will be enormous. You always try to include a threshold distance when using the inverse distance relationships. This is particularly important for large datasets. If you do not provide a threshold distance, one will be computed for you, but this may not be the most appropriate distance for your analysis. The default distance threshold will be the minimum distance that ensures every feature has at least one neighbor.
The Fixed distance band option works well for point data and is often a reasonable option for polygon data when there is a large variation in polygon size (very large polygons at the edge of the study area and very small polygons at the center of the study area, for example), and you want to ensure a consistent scale of analysis. See Best practices for selecting a fixed distance band value for strategies to help you determine an appropriate distance band value for your analysis.
The Zone of indifference option works well when fixed distance is appropriate but imposing sharp boundaries on neighborhood relationships is not an accurate representation of your data. The zone of indifference relationship considers every feature to be a neighbor of every other feature.
The polygon contiguity relationships (Contiguity edges only and Contiguity edges corners options) are effective when polygons are similar in size and distribution, and when spatial relationships are a function of polygon proximity (the idea that if two polygons share a boundary, spatial interaction between them increases). When you select a polygon contiguity conceptualization, you will almost always want to select row standardization for tools that have the Row Standardization parameter.
The K nearest neighbors option is effective when you want to ensure you have a minimum number of neighbors for your analysis. Especially when the values associated with your features are skewed (are not normally distributed), it is important that each feature is evaluated in the context of at least eight neighbors (this is a rule of thumb only). When the distribution of your data varies across your study area so that some features are far away from all other features, this method works well. Note, however, that the spatial context of your analysis changes depending on variations in the sparsity or density of your features. When fixing the scale of analysis is less important than fixing the number of neighbors, the K nearest neighbors method is appropriate.
The Delaunay triangulation option (sometimes called natural neighbors) option is appropriate when your data includes island polygons (isolated polygons that do not share any boundaries with other polygons) or in cases where there is a very uneven spatial distribution of features.
The Space time window option allows you to define feature relationships in terms of both their spatial and their temporal proximity. This option is appropriate, for example, to identify space-time hot spots or construct groups in which membership is constrained by space and time proximity. Examples of space-time analysis as well as strategies for effectively rendering the results from this type of analysis are provided in Space-Time Analysis.
For some applications, spatial interaction is best modeled in terms of travel time or travel distance. If you are modeling accessibility to urban services, for example, or looking for urban crime hot spots, modeling spatial relationships in terms of a network is recommended. Use the Generate Network Spatial Weights tool.
If none of the predefined options work well for your analysis, you can create an ASCII text file or table with the feature-to-feature relationships you want and use these to build a spatial weights matrix file. If one of the options above is close to your desired spatial relationship, you can use the Generate Spatial Weights Matrix tool to create a basic spatial weights matrix file, and edit your spatial weights matrix file.
Weighting schemes
While the inverse distance and zone of indifference spatial relationships directly apply weights to all neighbors based on distance, various tools allow you to specify a spatial relationship by first defining a neighborhood structure (like distance band or k nearest neighbors) and then specifying a method to apply weights to the neighbors. Similar to inverse distance weighting, it is common to assign higher weights to neighbors close to the focal feature using a function, called a kernel, that decreases with distance. Kernel weighting has the advantage of providing stable weights to neighbors at both near and far distances, whereas inverse distance weighting has problems at distances shorter than one, and the weights rapidly decrease moving away from the focal feature. All kernels must use a bandwidth that can be fixed or adaptive that defines how quickly the weights will decrease with distance. Common kernels include bisquare, Gaussian, triangular, and quadratic. See How Neighborhood Summary Statistics works to learn more about kernel weighting.
The Generate Spatial Weights Matrix tool additionally allows you to weight by the length of shared border when defining spatial relationships using polygon contiguity. This allows you to assign more influence to features that share a larger proportion of the border of the focal features. You can also weight by the values of a field, such as population or polygon area, to assign higher weights to features with higher field values. When weighting by shared border or field values, all weights will be row standardized.
Distance method
Several tools provide you with the choice of either Euclidean or Manhattan distance.
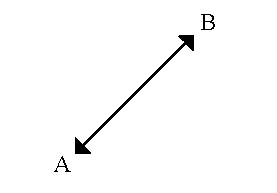
- Euclidean distance is calculated as
D = sq root [(x1–x2)**2.0 + (y1–y2)**2.0]where (x1, y1) is the coordinate for point A, (x2, y2) is the coordinate for point B, and D is the straight-line distance between points A and B.
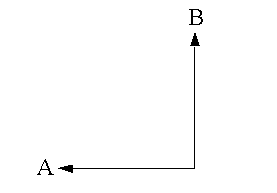
- Manhattan distance is calculated as
D = abs(x1–x2) + abs(y1–y2)where (x1, y1) is the coordinate for point A, (x2, y2) is the coordinate for point B, and D is the vertical plus horizontal difference between points A and B. It is the distance you must travel if you are restricted to north–south and east–west travel only. This method is generally more appropriate than Euclidean distance when travel is restricted to a street network and where actual street network travel costs are not available.
When your input features are not projected (that is, the coordinates are in latitude and longitude coordinates) or when the output coordinate system is set to a geographic coordinate system, distances will be computed using chordal measurements and the Distance Method parameter will be disabled. Chordal distance measurements are used because they can be computed quickly and provide accurate estimates of true geodesic distances, at least for points within about 30 degrees of each other. Chordal distances are based on a spherical earth model, and given any two points on the surface, the chordal distance between them is the 3D straight-line distance connecting them (this straight line will go through the earth). Chordal distances are reported in meters.
Caution:
It is recommended to project your data if your study area extends beyond 30 degrees. Chordal distances are not a reliable estimate of geodesic distances beyond 30 degrees.
Self-weighting
Several tools allow you to define features and weights as neighbors of themselves, called self-weighting. For example, you might use self-weights to reflect average intrazonal travel costs based on polygon size. The Hot Spot Analysis tool allows you to provide a field representing self-weights in the Self Potential Field parameter. The Generate Network Spatial Weights and Neighborhood Summary Statistics tools allow you to include self-weights using the Include Focal Feature parameter. Various other tools such as Bivariate Spatial Association (Lee's L) will automatically add self-weights to any provided spatial relationship.
Row standardization
Row standardization is recommended whenever the distribution of your features is potentially biased due to sampling design or an imposed aggregation scheme. When row standardization is selected, each weight is divided by its row sum (the sum of the weights of all neighboring features) so that the weights will sum to 1. Row standardized weighting is often used with fixed distance neighborhoods and almost always used for neighborhoods based on polygon contiguity. This is to mitigate bias due to features having different numbers of neighbors. Row standardization creates a relative, rather than absolute, weighting scheme that is appropriate, for example, when working with administrative boundaries.
Distance band
The Distance Band (sometimes called threshold distance) parameter sets the scale of analysis for most spatial relationships for various spatial relationships. Choosing an appropriate distance is important. Some spatial statistics require each feature to have at least one neighbor for the analysis to be reliable. If the distance band is too small (so that some features have no neighbors), a warning message will be returned. The Calculate Distance Band from Neighbor Count tool will evaluate minimum, average, and maximum distances for a specified number of neighbors and can help you determine an appropriate distance band value to use for analysis. See Best practices for selecting a fixed distance band value for additional guidelines.
When no value is specified, a default threshold distance is computed. The following table indicates how different spatial relationships behave for each of three possible input types (negative values are not valid):
| Inverse Distance, Inverse Distance Squared | Fixed Distance Band, Zone of Indifference | Polygon Contiguity, Delaunay Triangulation, K Nearest Neighbors | |
|---|---|---|---|
| 0 | No threshold or cutoff is applied; every feature is a neighbor of every other feature. | Invalid. A runtime error will be generated. | Ignored |
| empty | A default distance will be computed. This default will be the minimum distance to ensure that every feature has at least one neighbor. | A default distance will be computed. This default will be the minimum distance to ensure that every feature has at least one neighbor. | Ignored |
| positive number | The nonzero, positive value specified will be used as a cutoff distance; neighbor relationships will only exist among features within this distance of each other. | For fixed distance band, only features within this specified cutoff of each other will be neighbors. For zone of indifference, features within this specified cutoff of each other will be neighbors; features outside the cutoff are neighbors too, but they are assigned a smaller and smaller weight or influence as distance increases. | Ignored |
Number of neighbors
The Number of Neighbors parameter serves a purpose for various spatial relationships. For k nearest neighbors, each target feature will use the closest K features (where K is the number of neighbors specified). For inverse distance and distance band, the threshold distance will extend for feature to ensure that it has at least K features. For the polygon contiguity spatial relationships, additional neighbors will be added based on feature centroid proximity to ensure at least K neighbors.
Weights matrix text file
Several tools allow you to define spatial relationships among features by providing a spatial weights matrix (.swm) file. Spatial weights are numbers between 0 and 1 that reflect the interaction and influence between each feature and every other feature in the dataset. The spatial weights matrix file can be created using the Generate Spatial Weights Matrix tool or it can be a simple ASCII file.
When the spatial weights matrix file is a simple ASCII text file, the first line should be the name of a unique ID field. This gives you the flexibility to use any numeric field in your dataset as the ID when generating this file; however, the ID field must be type Integer (Long or Short) and have unique values for every feature. After the first line, the spatial weights file should be formatted into the following three columns:
- From feature ID
- To feature ID
- Weight
For example, suppose you have three gas stations. The field you are using as the ID field is called StationID, and the feature IDs are 1, 2, and 3. You want to model spatial relationships among these three gas stations using inverse travel time. The ASCII file might look like the following:

Typing the values for the spatial weights matrix file can be burdensome. A more efficient approach is to use the Generate Spatial Weights Matrix tool to create a spatial weights matrix file.
Spatial weights matrix file (.swm)
The Generate Spatial Weights Matrix tool will create a spatial weights matrix file (.swm) defining the spatial relationships among all the features in your dataset based on the parameters you specify. This file is created in binary file format so the values in the file cannot be viewed directly. To view or edit the feature relationships in an .swm file, use the Convert Spatial Weights Matrix To Table tool.
You can also use the Generate Spatial Weights Matrix tool to convert that table into a .swm file. The table requires the following fields:
| Field name | Description |
|---|---|
| <Unique ID field name> | An integer field that a unique for each feature. The name and type of the field must match an associated unique ID field of the features. For example, if a feature with ID 6 has four neighbors, the value 6 will be repeated four times in this field, once for each neighbor. |
| NID | An integer field containing the ID of the neighbor. |
| WEIGHT | A numeric weight between 0 and 1 representing the influence or interaction between the two features. |
The simplest way to edit a .swm file with custom weights is to create an initial .swm file and convert it to a table. This table will have the correct field names and properties, so you can create and edit rows to assign custom neighbor relationships and weights. The table must also be sorted by the unique ID and then the neighbor ID.
Sharing spatial weights matrix files
The output from the Generate Spatial Weights Matrix tool is an .swm file. This file is tied to the input feature class, the unique ID field, and the output coordinate system settings when the .swm file was created. Other people can duplicate the spatial relationships you define for analysis by using your .swm file and either the same input feature class or a feature class linking all or a subset of the features to a matching Unique ID field. Especially if you plan to share your .swm files with others, avoid using an output coordinate system that differs from the spatial reference of the original features. It is recommended that you project the input features feature first and create the spatial weights matrix file for the new spatial reference.
Network spatial weights
In some analyses, spatial relationships are better defined by travel distance along a network rather than straight-line proximity. For example, when modeling emergency response times, it may be more appropriate to define neighbors based on shortest-path travel time through a road network rather than Euclidean distance. For datasets like this, you can use the Generate Network Spatial Weights tool to define spatial relationships using a network dataset, defining spatial relationships in terms of the underlying network structure.