Mit der Spatial Analyst-Lizenz verfügbar.
Verschiedene Raster-Datasets müssen nicht mit der gleichen Zellenauflösung gespeichert werden. Bei der Bearbeitung verschiedener Datasets muss die Zellenauflösung jedoch, ebenso wie die Registrierung, gleich sein. Werden verschiedene Raster-Datasets mit unterschiedlichen Auflösungen in ein Werkzeug der Erweiterung "ArcGIS Spatial Analyst" eingegeben, wird für eines oder mehrere dieser Eingabe-Datasets automatisch ein Resampling zur gröbsten Auflösung für Eingabe-Datasets durchgeführt.
Standardmäßig wird die Resampling-Methode "nächster Nachbar" verwendet. Der Grund hierfür ist, dass diese Methode sowohl auf diskontinuierliche als auch auf kontinuierliche Wertetypen angewendet werden kann, während die bilineare Interpolation und die kubische Faltung als weitere Resampling-Methoden nur auf kontinuierliche Daten angewendet werden können. Eine der Resampling-Methoden ist jedoch erforderlich, da es selten vorkommt, dass sich die Zentren der Eingabezellen mit den transformierten Zellzentren der gewünschten Auflösung korrekt überlagern. Die bilineare und die kubische Methode können vor der Verarbeitung von Rastern mit unterschiedlicher Auflösung mithilfe des Werkzeugs Resampling als Vorbearbeitungsschritt angewandt werden.
Hinweis:
Bestimmte Werkzeuge wie die Werkzeuge im Toolset Oberfläche verwenden bilineare Interpolation als Standard-Interpolationsmethode. Weitere Informationen finden Sie in der jeweiligen Werkzeugreferenz.
Die Auflösung des Standard-Resampling kann mithilfe des Umgebungsparameters Zellengröße gesteuert werden, mit dem Sie angeben können, ob das Werkzeug entweder die minimale Auflösung der Eingabe-Raster oder eine bestimmte, von Ihnen festgelegte Zellengröße verwenden soll.
Hinweis:
Seien Sie bei der Festlegung von Zellengrößen, die feiner sind als die in den Eingabe-Raster-Datasets, besonders vorsichtig. Es werden keine neuen Daten erstellt. Zellen werden mit der Resampling-Methode "Nächster Nachbar" interpoliert. Das Ergebnis ist nur so genau wie die Eingabe mit der niedrigsten Auflösung. Eine eingegebene Zellengröße von 50 m bei Eingabe-Raster-Datasets von 100 m bewirkt ein Ausgabe-Raster mit einer Zellengröße von 50 m, obwohl die Genauigkeit immer noch bei 100 m liegt.
In der folgenden Abbildung ist die in der Analyseumgebung eingestellte Zellengröße höher als die Zellengröße des Eingabe-Rasters für das Werkzeug. Bei Ausführung wird das Eingabe-Raster zuerst zur niedrigeren Auflösung resampled und anschließend das Werkzeug angewendet.
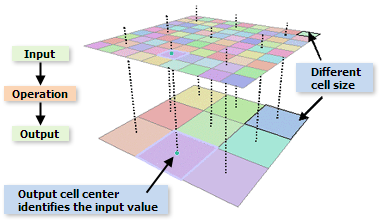
Bei der Durchführung der Analyse müssen Sie darauf achten, dass Sie eine passende Zellengröße angeben. Es ist beispielsweise unwahrscheinlich, dass Sie die Bewegungen von Mäusen untersuchen, wenn die Zellengröße fünf Kilometer beträgt. Eine Zellengröße von fünf Kilometern ist zweckmäßiger, wenn Sie beispielsweise die Auswirkungen der globalen Erwärmung auf die Erde untersuchen.
Resampling
Um den Wert zu finden, den jede Zelle auf dem Ausgabe-Raster erhalten sollte, wird das Zentrum jeder Zelle von der Ausgabe in das ursprüngliche Eingabe-Koordinatensystem eingetragen. Jede Koordinate eines Zellenmittelpunktes wird so zurück konvertiert, um die Position des Punktes im ursprünglichen Eingabe-Raster zu bestimmen. Sobald diese Eingabeposition festgelegt ist, kann der Ausgabeposition ein Wert anhand der benachbarten Zellen der Eingabe zugewiesen werden. Es passiert selten, dass ein Ausgabe-Zellenmittelpunkt lagegleich mit einem Zellenmittelpunkt des Eingabe-Rasters liegt. Daher wurden Methoden entwickelt, mit denen sich der Ausgabewert anhand der Position des Punktes in Bezug auf die Zellzentren des Eingabe-Rasters sowie abhängig vom Wert dieser Zellen ermitteln lässt. Die drei Methoden zur Bestimmung der Ausgabewerte sind Nächster-Nachbar-Resampling, bilineare Interpolation und kubische Faltung. Jede dieser Techniken weist der Ausgabe unterschiedliche Werte zu. Deshalb können die den Zellen eines Ausgabe-Rasters zugewiesenen Werte je nach verwendeter Technik unterschiedlich sein.
Nächster-Nachbar-Resampling
Nächster-Nachbar-Resampling ist die Resampling-Methode der Wahl für diskontinuierliche (kategorische) Daten, da sie den Wert der Eingabezellen nicht verändert. Wenn die Position des Zellenmittelpunktes auf dem Ausgabe-Raster-Dataset auch auf dem Eingabe-Raster bekannt ist, bestimmt diese Methode die Position des dichtesten Zellenmittelpunktes auf dem Eingabe-Raster und weist den Wert dieser Zelle der Zelle im Ausgabe-Raster zu.
Nächster-Nachbar-Resampling ändert nicht die Werte der Zellen des Eingabe-Raster-Datasets. Der Wert 2 im Eingabe-Raster bleibt auch im Ausgabe-Raster erhalten und wird nicht in 2,2 oder 2,3 geändert. Da die Ausgabezellenwerte unverändert bleiben, sollte das Nächster-Nachbar-Resampling für Nominal- oder Ordinaldaten verwendet werden, bei dem jeder Wert eine Klasse, ein Teil oder eine Klassifizierung (Kategoriedaten wie Landnutzungs-, Boden- oder Waldtyp) darstellt.
Erwägen Sie ein Ausgabe-Raster, das aus einem Eingabe-Raster erstellt wurde, das in einer Operation um 45° gedreht und auf diese Weise resampled wurde. Für jede Ausgabezelle muss ein Wert vom Eingabe-Raster abgeleitet werden. In der Abbildung unten sind die Zellenmittelpunkte des Eingabe-Rasters als graue Punkte dargestellt. Die Ausgabezellen sind grün dargestellt. Die Zelle, die verarbeitet wird, ist gelb dargestellt. Bei der Zuweisung des nächsten Nachbars wird der Zellenmittelpunkt (orangefarbener Punkt) im Eingabe-Raster identifiziert, der dem Zellenmittelpunkt der bearbeiteten Zelle (roter Punkt) in der Ausgabe am nächsten liegt, und als Ausgabewert für die bearbeitete Zelle (gelb) zugewiesen. Dieser Prozess wird für jede Zelle des Ausgabe-Rasters wiederholt. 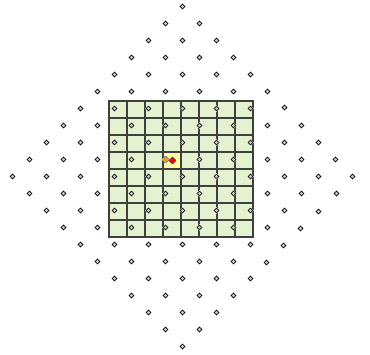
Bilineare Interpolation
Die bilineare Interpolation nutzt den Wert der vier dichtesten Eingabezellzentren, um den Wert auf dem Ausgabe-Raster zu bestimmen. Der neue Wert für die Ausgabezelle ist ein gewichteter Durchschnitt dieser vier Werte, der angepasst wurde, um die Entfernung dieser Zellen zum Zentrum der Ausgabezelle zu berücksichtigen. Diese Interpolationsmethode ergibt eine glatter aussehende Oberfläche als die, die aus der Methode "Nächster-Nachbar-Resampling" entstehen würde.
Ebenso wie bei der Nächster-Nachbar-Interpolation sind in der folgenden Abbildung die Zellenmittelpunkte des Eingabe-Rasters als graue Punkte dargestellt. Die Ausgabezellen sind grün, und die bearbeitete Zelle ist gelb unterlegt. Bei der bilinearen Interpolation werden die vier Zellenmittelpunkte (orangefarbene Punkte) bestimmt, die dem Zellenmittelpunkt der bearbeiteten Zelle (roter Punkt) am nächsten liegen. Der gewichtete Durchschnitt wird berechnet, und das Ergebnis wird als Ausgabewert der bearbeiteten Zelle (gelb) zugewiesen. 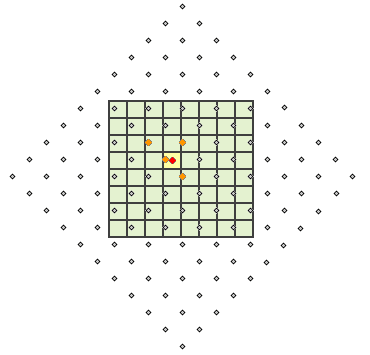
Da die Werte für die Ausgabezellen nach der relativen Position und dem Wert der Eingabezellen berechnet werden, wird die bilineare Interpolation bevorzugt für Daten verwendet, bei denen die Position eines bekannten Punktes oder eines geographischen Objektes den der Zelle zugewiesenen Wert bestimmt (d. h. kontinuierliche Oberflächen). Die Höhe, die Neigung, der Geräuschpegel eines Flughafens und der Salzgehalt des Grundwassers in der Nähe einer Flussmündung sind Phänomene, die als kontinuierliche Oberflächen dargestellt werden und bei denen mithilfe der bilinearen Interpolation ein sehr genaues Resampling durchgeführt wurde.
Kubische Faltung
Die kubische Faltung ähnelt der bilinearen Interpolation, außer dass hier der gewichtete Durchschnitt aus den 16 dichtesten Eingabezellzentren und deren Werten berechnet wird.
Die folgende Abbildung veranschaulicht die Berechnung des Ausgabewertes für die kubische Faltung. Es werden die sechzehn Zellenmittelpunkte (orange Punkte) bestimmt, die dem Zellenmittelpunkt der bearbeiteten Zelle (roter Punkt) am nächsten liegen. Anschließend wird der gewichtete Durchschnitt berechnet, und das Ergebnis wird als Ausgabewert der bearbeiteten Zelle (gelb) zugewiesen.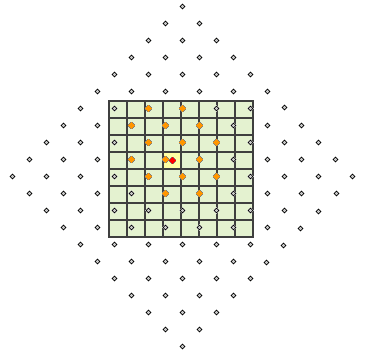
Die kubische Faltung tendiert dazu, die Daten in den Randbereichen mehr als die bilineare Interpolation zu schärfen, da mehr Zellen in die Berechnung des Ausgabewertes einbezogen werden.
Resampling und Datentypen
Die bilineare Interpolation oder die kubische Faltung sollten nicht für Kategoriedaten verwendet werden, da die Kategorien im Ausgabe-Raster-Dataset nicht erhalten bleiben. Alle drei Methoden können jedoch für kontinuierliche Daten verwendet werden, wobei die Methode Nächster-Nachbar-Resampling eine blockförmige Ausgabe, die bilineare Interpolation glattere Ergebnisse und die kubische Faltung die Ergebnisse mit scharfer Ausprägung liefert.